between groups quasi experimental

8.2 Non-Equivalent Groups Designs

Learning objectives.

• Describe the different types of nonequivalent groups quasi-experimental designs.
• Identify some of the threats to internal validity associated with each of these designs. 

Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A  nonequivalent groups design , then, is a between-subjects design in which participants have not been randomly assigned to conditions. There are several types of nonequivalent groups designs we will consider.

Posttest Only Nonequivalent Groups Design

The first nonequivalent groups design we will consider is the posttest only nonequivalent groups design.  In this design, participants in one group are exposed to a treatment, a nonequivalent group is not exposed to the treatment, and then the two groups are compared. Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This design would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.

Of course, researchers using a posttest only nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.

Pretest-Posttest Nonequivalent Groups Design

Another way to improve upon the posttest only nonequivalent groups design is to add a pretest. In the  pretest-posttest nonequivalent groups design t here is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a nonequivalent control group that is given a pretest, does  not  receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve, but whether they improve  more  than participants who do not receive the treatment.

Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an anti-drug program, and finally, are given a posttest. Students in a similar school are given the pretest, not exposed to an anti-drug program, and finally, are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this change in attitude could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.

Returning to the example of evaluating a new measure of teaching third graders, this study could be improved by adding a pretest of students’ knowledge of fractions. The changes in scores from pretest to posttest would then be evaluated and compared across conditions to determine whether one group demonstrated a bigger improvement in knowledge of fractions than another. Of course, the teachers’ styles, and even the classroom environments might still be very different and might cause different levels of achievement or motivation among the students that are independent of the teaching intervention. Once again, differential history also represents a potential threat to internal validity.  If asbestos is found in one of the schools causing it to be shut down for a month then this interruption in teaching could produce a difference across groups on posttest scores.

If participants in this kind of design are randomly assigned to conditions, it becomes a true between-groups experiment rather than a quasi-experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.

Interrupted Time-Series Design with Nonequivalent Groups

One way to improve upon the interrupted time-series design is to add a control group. The interrupted time-series design with nonequivalent groups involves taking  a set of measurements at intervals over a period of time both before and after an intervention of interest in two or more nonequivalent groups. Once again consider the manufacturing company that measures its workers’ productivity each week for a year before and after reducing work shifts from 10 hours to 8 hours. This design could be improved by locating another manufacturing company who does not plan to change their shift length and using them as a nonequivalent control group. If productivity  increased rather quickly after the shortening of the work shifts in the treatment group but productivity remained consistent in the control group, then this provides better evidence for the effectiveness of the treatment. 

Similarly, in the example of examining the effects of taking attendance on student absences in a research methods course, the design could be improved by using students in another section of the research methods course as a control group. If a consistently higher number of absences was found in the treatment group before the intervention, followed by a sustained drop in absences after the treatment, while the nonequivalent control group showed consistently high absences across the semester then this would provide superior evidence for the effectiveness of the treatment in reducing absences.

Pretest-Posttest Design With Switching Replication

Some of these nonequivalent control group designs can be further improved by adding a switching replication. Using a pretest-posttest design with switching replication design, nonequivalent groups are administered a pretest of the dependent variable, then one group receives a treatment while a nonequivalent control group does not receive a treatment, the dependent variable is assessed again, and then the treatment is added to the control group, and finally the dependent variable is assessed one last time.

As a concrete example, let’s say we wanted to introduce an exercise intervention for the treatment of depression. We recruit one group of patients experiencing depression and a nonequivalent control group of students experiencing depression. We first measure depression levels in both groups, and then we introduce the exercise intervention to the patients experiencing depression, but we hold off on introducing the treatment to the students. We then measure depression levels in both groups. If the treatment is effective we should see a reduction in the depression levels of the patients (who received the treatment) but not in the students (who have not yet received the treatment). Finally, while the group of patients continues to engage in the treatment, we would introduce the treatment to the students with depression. Now and only now should we see the students’ levels of depression decrease.

One of the strengths of this design is that it includes a built in replication. In the example given, we would get evidence for the efficacy of the treatment in two different samples (patients and students). Another strength of this design is that it provides more control over history effects. It becomes rather unlikely that some outside event would perfectly coincide with the introduction of the treatment in the first group and with the delayed introduction of the treatment in the second group. For instance, if a change in the weather occurred when we first introduced the treatment to the patients, and this explained their reductions in depression the second time that depression was measured, then we would see depression levels decrease in both the groups. Similarly, the switching replication helps to control for maturation and instrumentation. Both groups would be expected to show the same rates of spontaneous remission of depression and if the instrument for assessing depression happened to change at some point in the study the change would be consistent across both of the groups. Of course, demand characteristics, placebo effects, and experimenter expectancy effects can still be problems. But they can be controlled for using some of the methods described in Chapter 5.

Switching Replication with Treatment Removal Design

In a basic pretest-posttest design with switching replication, the first group receives a treatment and the second group receives the same treatment a little bit later on (while the initial group continues to receive the treatment). In contrast, in a switching replication with treatment removal design , the treatment is removed from the first group when it is added to the second group. Once again, let’s assume we first measure the depression levels of patients with depression and students with depression. Then we introduce the exercise intervention to only the patients. After they have been exposed to the exercise intervention for a week we assess depression levels again in both groups. If the intervention is effective then we should see depression levels decrease in the patient group but not the student group (because the students haven’t received the treatment yet). Next, we would remove the treatment from the group of patients with depression. So we would tell them to stop exercising. At the same time, we would tell the student group to start exercising. After a week of the students exercising and the patients not exercising, we would reassess depression levels. Now if the intervention is effective we should see that the depression levels have decreased in the student group but that they have increased in the patient group (because they are no longer exercising).

Demonstrating a treatment effect in two groups staggered over time and demonstrating the reversal of the treatment effect after the treatment has been removed can provide strong evidence for the efficacy of the treatment. In addition to providing evidence for the replicability of the findings, this design can also provide evidence for whether the treatment continues to show effects after it has been withdrawn.

Key Takeaways

• Quasi-experimental research involves the manipulation of an independent variable without the random assignment of participants to conditions or counterbalancing of orders of conditions.
• There are three types of quasi-experimental designs that are within-subjects in nature. These are the one-group posttest only design, the one-group pretest-posttest design, and the interrupted time-series design.
• There are five types of quasi-experimental designs that are between-subjects in nature. These are the posttest only design with nonequivalent groups, the pretest-posttest design with nonequivalent groups, the interrupted time-series design with nonequivalent groups, the pretest-posttest design with switching replication, and the switching replication with treatment removal design.
• Quasi-experimental research eliminates the directionality problem because it involves the manipulation of the independent variable. However, it does not eliminate the problem of confounding variables, because it does not involve random assignment to conditions or counterbalancing. For these reasons, quasi-experimental research is generally higher in internal validity than non-experimental studies but lower than true experiments.
• Of all of the quasi-experimental designs, those that include a switching replication are highest in internal validity.
• Practice: Imagine that two professors decide to test the effect of giving daily quizzes on student performance in a statistics course. They decide that Professor A will give quizzes but Professor B will not. They will then compare the performance of students in their two sections on a common final exam. List five other variables that might differ between the two sections that could affect the results.
• regression to the mean
• spontaneous remission

Share This Book

• Increase Font Size

• Privacy Policy

Home » Quasi-Experimental Research Design – Types, Methods

Quasi-Experimental Research Design – Types, Methods

Table of Contents

Quasi-experimental research design is a widely used methodology in social sciences, education, healthcare, and other fields to evaluate the impact of an intervention or treatment. Unlike true experimental designs, quasi-experiments lack random assignment, which can limit control over external factors but still offer valuable insights into cause-and-effect relationships.

This article delves into the concept of quasi-experimental research, explores its types, methods, and applications, and discusses its strengths and limitations.

Quasi-Experimental Design

Quasi-experimental research design is a type of empirical study used to estimate the causal relationship between an intervention and its outcomes. It resembles an experimental design but does not involve random assignment of participants to groups. Instead, groups are pre-existing or assigned based on non-random criteria, such as location, demographic characteristics, or convenience.

For example, a school might implement a new teaching method in one class while another class continues with the traditional approach. Researchers can then compare the outcomes to assess the effectiveness of the new method.

Key Characteristics of Quasi-Experimental Research

• No Random Assignment: Participants are not randomly assigned to experimental or control groups.
• Comparison Groups: Often involves comparing a treatment group to a non-equivalent control group.
• Real-World Settings: Frequently conducted in natural environments, such as schools, hospitals, or workplaces.
• Causal Inference: Aims to identify causal relationships, though less robustly than true experiments.

Purpose of Quasi-Experimental Research

• To evaluate interventions or treatments when randomization is impractical or unethical.
• To provide evidence of causality in real-world settings.
• To test hypotheses and inform policies or practices.

Types of Quasi-Experimental Research Design

1. non-equivalent groups design (negd).

In this design, the researcher compares outcomes between a treatment group and a control group that are not randomly assigned.

• Example: Comparing student performance in schools that adopt a new curriculum versus those that do not.
• Limitation: Potential selection bias due to differences between the groups.

2. Time-Series Design

This involves repeatedly measuring the outcome variable before and after the intervention to observe trends over time.

• Example: Monitoring air pollution levels before and after implementing an industrial emission regulation.
• Variation: Interrupted time-series design, which identifies significant changes at specific intervention points.

3. Regression Discontinuity Design (RDD)

Participants are assigned to treatment or control groups based on a predetermined cutoff score on a continuous variable.

• Example: Evaluating the effect of a scholarship program where students with test scores above a threshold receive funding.
• Strength: Stronger causal inference compared to other quasi-experimental designs.

4. Pretest-Posttest Design

In this design, outcomes are measured before and after the intervention within the same group.

• Example: Assessing the effectiveness of a training program by comparing employees’ skills before and after the training.
• Limitation: Vulnerable to confounding factors that may influence results independently of the intervention.

5. Propensity Score Matching (PSM)

This method pairs participants in the treatment and control groups based on similar characteristics to reduce selection bias.

• Example: Evaluating the impact of online learning by matching students based on demographics and prior academic performance.
• Strength: Improves comparability between groups.

Methods of Quasi-Experimental Research

1. data collection.

• Surveys: Collect information on attitudes, behaviors, or outcomes related to the intervention.
• Observations: Document changes in natural environments or behaviors over time.
• Archival Data: Use pre-existing data, such as medical records or academic scores, to analyze outcomes.

2. Statistical Analysis

Quasi-experiments rely on statistical techniques to control for confounding variables and enhance the validity of results.

• Analysis of Covariance (ANCOVA): Controls for pre-existing differences between groups.
• Regression Analysis: Identifies relationships between the intervention and outcomes while accounting for other factors.
• Propensity Score Matching: Balances treatment and control groups to reduce bias.

3. Control for Confounding Variables

Because randomization is absent, quasi-experimental designs must address confounders using techniques like:

• Matching: Pair participants with similar attributes.
• Stratification: Analyze subgroups based on characteristics like age or income.
• Sensitivity Analysis: Test how robust findings are to potential biases.

4. Use of Mixed Methods

Combining quantitative and qualitative methods enhances the depth of analysis.

• Quantitative: Statistical tests to measure effect size.
• Qualitative: Interviews or focus groups to understand contextual factors influencing outcomes.

Applications of Quasi-Experimental Research

1. education.

• Assessing the impact of new teaching methods or curricula.
• Evaluating the effectiveness of after-school programs on academic performance.

2. Healthcare

• Comparing outcomes of different treatment protocols in hospitals.
• Studying the impact of public health campaigns on vaccination rates.

3. Policy Analysis

• Measuring the effects of new laws or regulations, such as minimum wage increases.
• Evaluating the impact of urban planning initiatives on community health.

4. Social Sciences

• Studying the influence of community programs on crime rates.
• Analyzing the effect of workplace interventions on employee satisfaction.

Strengths of Quasi-Experimental Research

• Feasibility: Can be conducted in real-world settings where randomization is impractical or unethical.
• Cost-Effectiveness: Often requires fewer resources compared to true experiments.
• Flexibility: Accommodates a variety of contexts and research questions.
• Generates Evidence: Provides valuable insights into causal relationships.

Limitations of Quasi-Experimental Research

• Potential Bias: Lack of randomization increases the risk of selection bias.
• Confounding Variables: Results may be influenced by external factors unrelated to the intervention.
• Limited Generalizability: Findings may not apply broadly due to non-random group assignment.
• Weaker Causality: Less robust in establishing causation compared to randomized controlled trials.

Steps to Conduct Quasi-Experimental Research

• Define the Research Question: Clearly articulate what you aim to study and why a quasi-experimental design is appropriate.
• Identify Comparison Groups: Select treatment and control groups based on the research context.
• Collect Data: Use surveys, observations, or archival records to gather pre- and post-intervention data.
• Control for Confounders: Employ statistical methods or matching techniques to address potential biases.
• Analyze Results: Use appropriate statistical tools to evaluate the intervention’s impact.
• Interpret Findings: Discuss results in light of limitations and potential confounding factors.

Quasi-experimental research design offers a practical and versatile approach for evaluating interventions when randomization is not feasible. By employing methods such as non-equivalent groups design, time-series analysis, and regression discontinuity, researchers can draw meaningful conclusions about causal relationships. While these designs may have limitations in controlling bias and confounding variables, careful planning, robust statistical techniques, and clear reporting can enhance their validity and impact. Quasi-experiments are invaluable in fields like education, healthcare, and policy analysis, providing actionable insights for real-world challenges.

• Cook, T. D., & Campbell, D. T. (1979). Quasi-Experimentation: Design and Analysis Issues for Field Settings . Houghton Mifflin.
• Shadish, W. R., Cook, T. D., & Campbell, D. T. (2002). Experimental and Quasi-Experimental Designs for Generalized Causal Inference . Houghton Mifflin.
• Creswell, J. W. (2018). Research Design: Qualitative, Quantitative, and Mixed Methods Approaches . Sage Publications.
• Bryman, A. (2016). Social Research Methods . Oxford University Press.
• Babbie, E. (2020). The Practice of Social Research . Cengage Learning.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Questionnaire – Definition, Types, and Examples

Ethnographic Research -Types, Methods and Guide

Phenomenology – Methods, Examples and Guide

Observational Research – Methods and Guide

Applied Research – Types, Methods and Examples

Correlational Research – Methods, Types and...

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7.3 Quasi-Experimental Research

Learning objectives.

• Explain what quasi-experimental research is and distinguish it clearly from both experimental and correlational research.
• Describe three different types of quasi-experimental research designs (nonequivalent groups, pretest-posttest, and interrupted time series) and identify examples of each one.

The prefix quasi means “resembling.” Thus quasi-experimental research is research that resembles experimental research but is not true experimental research. Although the independent variable is manipulated, participants are not randomly assigned to conditions or orders of conditions (Cook & Campbell, 1979). Because the independent variable is manipulated before the dependent variable is measured, quasi-experimental research eliminates the directionality problem. But because participants are not randomly assigned—making it likely that there are other differences between conditions—quasi-experimental research does not eliminate the problem of confounding variables. In terms of internal validity, therefore, quasi-experiments are generally somewhere between correlational studies and true experiments.

Quasi-experiments are most likely to be conducted in field settings in which random assignment is difficult or impossible. They are often conducted to evaluate the effectiveness of a treatment—perhaps a type of psychotherapy or an educational intervention. There are many different kinds of quasi-experiments, but we will discuss just a few of the most common ones here.

Nonequivalent Groups Design

Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A nonequivalent groups design , then, is a between-subjects design in which participants have not been randomly assigned to conditions.

Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments, might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.

Of course, researchers using a nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.

Pretest-Posttest Design

In a pretest-posttest design , the dependent variable is measured once before the treatment is implemented and once after it is implemented. Imagine, for example, a researcher who is interested in the effectiveness of an antidrug education program on elementary school students’ attitudes toward illegal drugs. The researcher could measure the attitudes of students at a particular elementary school during one week, implement the antidrug program during the next week, and finally, measure their attitudes again the following week. The pretest-posttest design is much like a within-subjects experiment in which each participant is tested first under the control condition and then under the treatment condition. It is unlike a within-subjects experiment, however, in that the order of conditions is not counterbalanced because it typically is not possible for a participant to be tested in the treatment condition first and then in an “untreated” control condition.

If the average posttest score is better than the average pretest score, then it makes sense to conclude that the treatment might be responsible for the improvement. Unfortunately, one often cannot conclude this with a high degree of certainty because there may be other explanations for why the posttest scores are better. One category of alternative explanations goes under the name of history . Other things might have happened between the pretest and the posttest. Perhaps an antidrug program aired on television and many of the students watched it, or perhaps a celebrity died of a drug overdose and many of the students heard about it. Another category of alternative explanations goes under the name of maturation . Participants might have changed between the pretest and the posttest in ways that they were going to anyway because they are growing and learning. If it were a yearlong program, participants might become less impulsive or better reasoners and this might be responsible for the change.

Another alternative explanation for a change in the dependent variable in a pretest-posttest design is regression to the mean . This refers to the statistical fact that an individual who scores extremely on a variable on one occasion will tend to score less extremely on the next occasion. For example, a bowler with a long-term average of 150 who suddenly bowls a 220 will almost certainly score lower in the next game. Her score will “regress” toward her mean score of 150. Regression to the mean can be a problem when participants are selected for further study because of their extreme scores. Imagine, for example, that only students who scored especially low on a test of fractions are given a special training program and then retested. Regression to the mean all but guarantees that their scores will be higher even if the training program has no effect. A closely related concept—and an extremely important one in psychological research—is spontaneous remission . This is the tendency for many medical and psychological problems to improve over time without any form of treatment. The common cold is a good example. If one were to measure symptom severity in 100 common cold sufferers today, give them a bowl of chicken soup every day, and then measure their symptom severity again in a week, they would probably be much improved. This does not mean that the chicken soup was responsible for the improvement, however, because they would have been much improved without any treatment at all. The same is true of many psychological problems. A group of severely depressed people today is likely to be less depressed on average in 6 months. In reviewing the results of several studies of treatments for depression, researchers Michael Posternak and Ivan Miller found that participants in waitlist control conditions improved an average of 10 to 15% before they received any treatment at all (Posternak & Miller, 2001). Thus one must generally be very cautious about inferring causality from pretest-posttest designs.

Does Psychotherapy Work?

Early studies on the effectiveness of psychotherapy tended to use pretest-posttest designs. In a classic 1952 article, researcher Hans Eysenck summarized the results of 24 such studies showing that about two thirds of patients improved between the pretest and the posttest (Eysenck, 1952). But Eysenck also compared these results with archival data from state hospital and insurance company records showing that similar patients recovered at about the same rate without receiving psychotherapy. This suggested to Eysenck that the improvement that patients showed in the pretest-posttest studies might be no more than spontaneous remission. Note that Eysenck did not conclude that psychotherapy was ineffective. He merely concluded that there was no evidence that it was, and he wrote of “the necessity of properly planned and executed experimental studies into this important field” (p. 323). You can read the entire article here:

http://psychclassics.yorku.ca/Eysenck/psychotherapy.htm

Fortunately, many other researchers took up Eysenck’s challenge, and by 1980 hundreds of experiments had been conducted in which participants were randomly assigned to treatment and control conditions, and the results were summarized in a classic book by Mary Lee Smith, Gene Glass, and Thomas Miller (Smith, Glass, & Miller, 1980). They found that overall psychotherapy was quite effective, with about 80% of treatment participants improving more than the average control participant. Subsequent research has focused more on the conditions under which different types of psychotherapy are more or less effective.

In a classic 1952 article, researcher Hans Eysenck pointed out the shortcomings of the simple pretest-posttest design for evaluating the effectiveness of psychotherapy.

Wikimedia Commons – CC BY-SA 3.0.

Interrupted Time Series Design

A variant of the pretest-posttest design is the interrupted time-series design . A time series is a set of measurements taken at intervals over a period of time. For example, a manufacturing company might measure its workers’ productivity each week for a year. In an interrupted time series-design, a time series like this is “interrupted” by a treatment. In one classic example, the treatment was the reduction of the work shifts in a factory from 10 hours to 8 hours (Cook & Campbell, 1979). Because productivity increased rather quickly after the shortening of the work shifts, and because it remained elevated for many months afterward, the researcher concluded that the shortening of the shifts caused the increase in productivity. Notice that the interrupted time-series design is like a pretest-posttest design in that it includes measurements of the dependent variable both before and after the treatment. It is unlike the pretest-posttest design, however, in that it includes multiple pretest and posttest measurements.

Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows data from a hypothetical interrupted time-series study. The dependent variable is the number of student absences per week in a research methods course. The treatment is that the instructor begins publicly taking attendance each day so that students know that the instructor is aware of who is present and who is absent. The top panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment worked. There is a consistently high number of absences before the treatment, and there is an immediate and sustained drop in absences after the treatment. The bottom panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment did not work. On average, the number of absences after the treatment is about the same as the number before. This figure also illustrates an advantage of the interrupted time-series design over a simpler pretest-posttest design. If there had been only one measurement of absences before the treatment at Week 7 and one afterward at Week 8, then it would have looked as though the treatment were responsible for the reduction. The multiple measurements both before and after the treatment suggest that the reduction between Weeks 7 and 8 is nothing more than normal week-to-week variation.

Figure 7.5 A Hypothetical Interrupted Time-Series Design

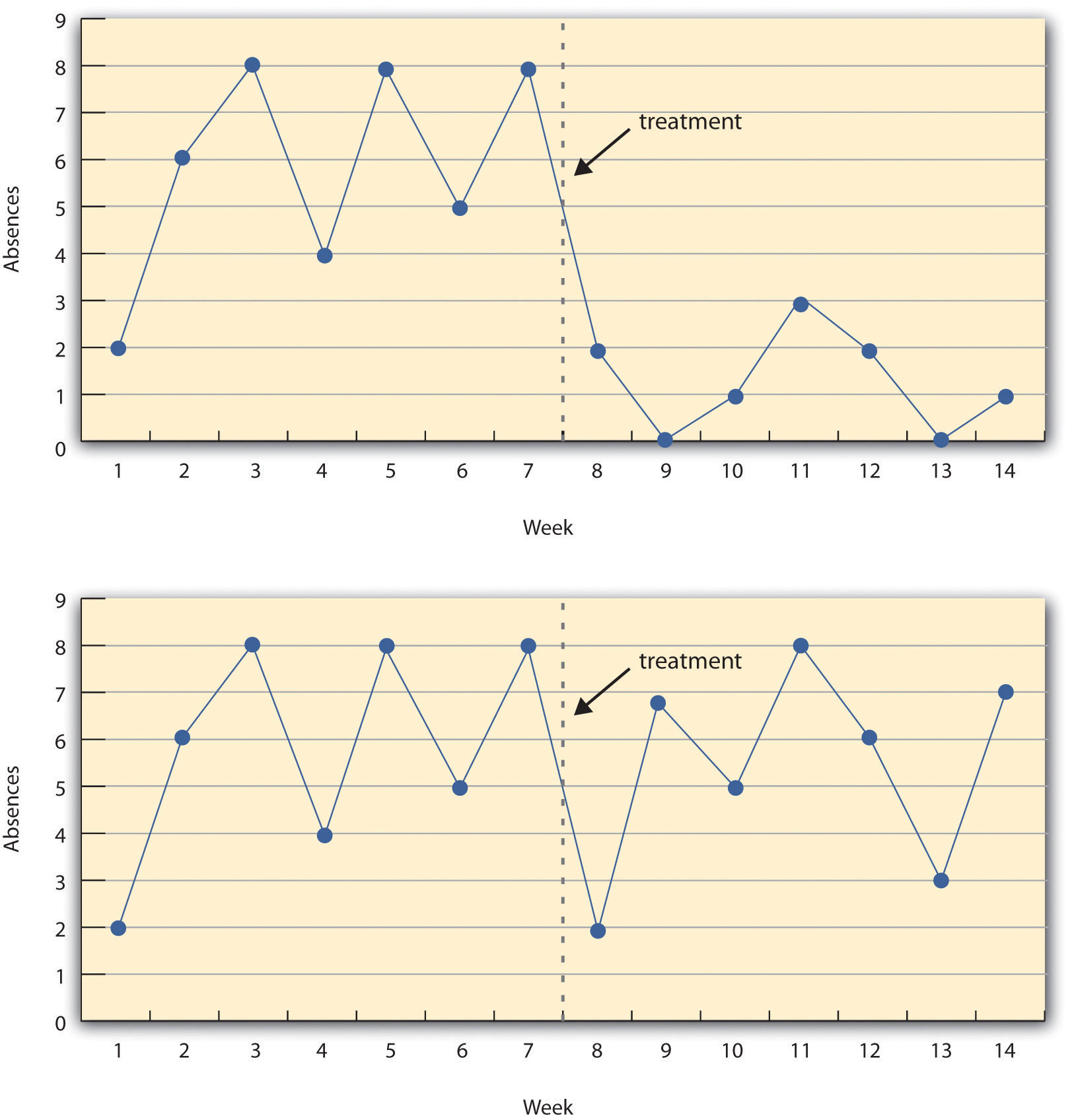
The top panel shows data that suggest that the treatment caused a reduction in absences. The bottom panel shows data that suggest that it did not.

Combination Designs

A type of quasi-experimental design that is generally better than either the nonequivalent groups design or the pretest-posttest design is one that combines elements of both. There is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a control group that is given a pretest, does not receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve but whether they improve more than participants who do not receive the treatment.

Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an antidrug program, and finally are given a posttest. Students in a similar school are given the pretest, not exposed to an antidrug program, and finally are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.

Finally, if participants in this kind of design are randomly assigned to conditions, it becomes a true experiment rather than a quasi experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.

Key Takeaways

• Quasi-experimental research involves the manipulation of an independent variable without the random assignment of participants to conditions or orders of conditions. Among the important types are nonequivalent groups designs, pretest-posttest, and interrupted time-series designs.
• Quasi-experimental research eliminates the directionality problem because it involves the manipulation of the independent variable. It does not eliminate the problem of confounding variables, however, because it does not involve random assignment to conditions. For these reasons, quasi-experimental research is generally higher in internal validity than correlational studies but lower than true experiments.
• Practice: Imagine that two college professors decide to test the effect of giving daily quizzes on student performance in a statistics course. They decide that Professor A will give quizzes but Professor B will not. They will then compare the performance of students in their two sections on a common final exam. List five other variables that might differ between the two sections that could affect the results.

Discussion: Imagine that a group of obese children is recruited for a study in which their weight is measured, then they participate for 3 months in a program that encourages them to be more active, and finally their weight is measured again. Explain how each of the following might affect the results:

• regression to the mean
• spontaneous remission

Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin.

Eysenck, H. J. (1952). The effects of psychotherapy: An evaluation. Journal of Consulting Psychology, 16 , 319–324.

Posternak, M. A., & Miller, I. (2001). Untreated short-term course of major depression: A meta-analysis of studies using outcomes from studies using wait-list control groups. Journal of Affective Disorders, 66 , 139–146.

Smith, M. L., Glass, G. V., & Miller, T. I. (1980). The benefits of psychotherapy . Baltimore, MD: Johns Hopkins University Press.

Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Child Care and Early Education Research Connections

Experiments and quasi-experiments.

This page includes an explanation of the types, key components, validity, ethics, and advantages and disadvantages of experimental design.

An experiment is a study in which the researcher manipulates the level of some independent variable and then measures the outcome. Experiments are powerful techniques for evaluating cause-and-effect relationships. Many researchers consider experiments the "gold standard" against which all other research designs should be judged. Experiments are conducted both in the laboratory and in real life situations.

Types of Experimental Design

There are two basic types of research design:

• True experiments
• Quasi-experiments

The purpose of both is to examine the cause of certain phenomena.

True experiments, in which all the important factors that might affect the phenomena of interest are completely controlled, are the preferred design. Often, however, it is not possible or practical to control all the key factors, so it becomes necessary to implement a quasi-experimental research design.

Similarities between true and quasi-experiments:

• Study participants are subjected to some type of treatment or condition
• Some outcome of interest is measured
• The researchers test whether differences in this outcome are related to the treatment

Differences between true experiments and quasi-experiments:

• In a true experiment, participants are randomly assigned to either the treatment or the control group, whereas they are not assigned randomly in a quasi-experiment
• In a quasi-experiment, the control and treatment groups differ not only in terms of the experimental treatment they receive, but also in other, often unknown or unknowable, ways. Thus, the researcher must try to statistically control for as many of these differences as possible
• Because control is lacking in quasi-experiments, there may be several "rival hypotheses" competing with the experimental manipulation as explanations for observed results

Key Components of Experimental Research Design

The manipulation of predictor variables.

In an experiment, the researcher manipulates the factor that is hypothesized to affect the outcome of interest. The factor that is being manipulated is typically referred to as the treatment or intervention. The researcher may manipulate whether research subjects receive a treatment (e.g., antidepressant medicine: yes or no) and the level of treatment (e.g., 50 mg, 75 mg, 100 mg, and 125 mg).

Suppose, for example, a group of researchers was interested in the causes of maternal employment. They might hypothesize that the provision of government-subsidized child care would promote such employment. They could then design an experiment in which some subjects would be provided the option of government-funded child care subsidies and others would not. The researchers might also manipulate the value of the child care subsidies in order to determine if higher subsidy values might result in different levels of maternal employment.

Random Assignment

• Study participants are randomly assigned to different treatment groups
• All participants have the same chance of being in a given condition
• Participants are assigned to either the group that receives the treatment, known as the "experimental group" or "treatment group," or to the group which does not receive the treatment, referred to as the "control group"
• Random assignment neutralizes factors other than the independent and dependent variables, making it possible to directly infer cause and effect

Random Sampling

Traditionally, experimental researchers have used convenience sampling to select study participants. However, as research methods have become more rigorous, and the problems with generalizing from a convenience sample to the larger population have become more apparent, experimental researchers are increasingly turning to random sampling. In experimental policy research studies, participants are often randomly selected from program administrative databases and randomly assigned to the control or treatment groups.

Validity of Results

The two types of validity of experiments are internal and external. It is often difficult to achieve both in social science research experiments.

Internal Validity

• When an experiment is internally valid, we are certain that the independent variable (e.g., child care subsidies) caused the outcome of the study (e.g., maternal employment)
• When subjects are randomly assigned to treatment or control groups, we can assume that the independent variable caused the observed outcomes because the two groups should not have differed from one another at the start of the experiment
• For example, take the child care subsidy example above. Since research subjects were randomly assigned to the treatment (child care subsidies available) and control (no child care subsidies available) groups, the two groups should not have differed at the outset of the study. If, after the intervention, mothers in the treatment group were more likely to be working, we can assume that the availability of child care subsidies promoted maternal employment

One potential threat to internal validity in experiments occurs when participants either drop out of the study or refuse to participate in the study. If particular types of individuals drop out or refuse to participate more often than individuals with other characteristics, this is called differential attrition. For example, suppose an experiment was conducted to assess the effects of a new reading curriculum. If the new curriculum was so tough that many of the slowest readers dropped out of school, the school with the new curriculum would experience an increase in the average reading scores. The reason they experienced an increase in reading scores, however, is because the worst readers left the school, not because the new curriculum improved students' reading skills.

External Validity

• External validity is also of particular concern in social science experiments
• It can be very difficult to generalize experimental results to groups that were not included in the study
• Studies that randomly select participants from the most diverse and representative populations are more likely to have external validity
• The use of random sampling techniques makes it easier to generalize the results of studies to other groups

For example, a research study shows that a new curriculum improved reading comprehension of third-grade children in Iowa. To assess the study's external validity, you would ask whether this new curriculum would also be effective with third graders in New York or with children in other elementary grades.

Glossary terms related to validity:

• internal validity
• external validity
• differential attrition

It is particularly important in experimental research to follow ethical guidelines. Protecting the health and safety of research subjects is imperative. In order to assure subject safety, all researchers should have their project reviewed by the Institutional Review Boards (IRBS). The  National Institutes of Health  supplies strict guidelines for project approval. Many of these guidelines are based on the  Belmont Report  (pdf).

The basic ethical principles:

• Respect for persons  -- requires that research subjects are not coerced into participating in a study and requires the protection of research subjects who have diminished autonomy
• Beneficence  -- requires that experiments do not harm research subjects, and that researchers minimize the risks for subjects while maximizing the benefits for them
• Justice  -- requires that all forms of differential treatment among research subjects be justified

Advantages and Disadvantages of Experimental Design

The environment in which the research takes place can often be carefully controlled. Consequently, it is easier to estimate the true effect of the variable of interest on the outcome of interest.

Disadvantages

It is often difficult to assure the external validity of the experiment, due to the frequently nonrandom selection processes and the artificial nature of the experimental context.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

The Use and Interpretation of Quasi-Experimental Studies in Medical Informatics

Anthony d harris , md, mph, jessina c mcgregor , phd, eli n perencevich , md, ms, jon p furuno , phd, jingkun zhu , ms, dan e peterson , md, mph, joseph finkelstein , md.

• Author information
• Article notes
• Copyright and License information

Correspondence and reprints: Anthony D. Harris, MD, MPH, Division of Healthcare Outcomes Research, Department of Epidemiology and Preventive Medicine, University of Maryland School of Medicine, 100 N. Greene Street, Lower Level, Baltimore, MD; e-mail: < [email protected] >.

Received 2004 Nov 19; Accepted 2005 Aug 12.

Quasi-experimental study designs, often described as nonrandomized, pre-post intervention studies, are common in the medical informatics literature. Yet little has been written about the benefits and limitations of the quasi-experimental approach as applied to informatics studies. This paper outlines a relative hierarchy and nomenclature of quasi-experimental study designs that is applicable to medical informatics intervention studies. In addition, the authors performed a systematic review of two medical informatics journals, the Journal of the American Medical Informatics Association (JAMIA) and the International Journal of Medical Informatics (IJMI), to determine the number of quasi-experimental studies published and how the studies are classified on the above-mentioned relative hierarchy. They hope that future medical informatics studies will implement higher level quasi-experimental study designs that yield more convincing evidence for causal links between medical informatics interventions and outcomes.

Quasi-experimental studies encompass a broad range of nonrandomized intervention studies. These designs are frequently used when it is not logistically feasible or ethical to conduct a randomized controlled trial. Examples of quasi-experimental studies follow. As one example of a quasi-experimental study, a hospital introduces a new order-entry system and wishes to study the impact of this intervention on the number of medication-related adverse events before and after the intervention. As another example, an informatics technology group is introducing a pharmacy order-entry system aimed at decreasing pharmacy costs. The intervention is implemented and pharmacy costs before and after the intervention are measured.

In medical informatics, the quasi-experimental, sometimes called the pre-post intervention, design often is used to evaluate the benefits of specific interventions. The increasing capacity of health care institutions to collect routine clinical data has led to the growing use of quasi-experimental study designs in the field of medical informatics as well as in other medical disciplines. However, little is written about these study designs in the medical literature or in traditional epidemiology textbooks. 1 , 2 , 3 In contrast, the social sciences literature is replete with examples of ways to implement and improve quasi-experimental studies. 4 , 5 , 6

In this paper, we review the different pretest-posttest quasi-experimental study designs, their nomenclature, and the relative hierarchy of these designs with respect to their ability to establish causal associations between an intervention and an outcome. The example of a pharmacy order-entry system aimed at decreasing pharmacy costs will be used throughout this article to illustrate the different quasi-experimental designs. We discuss limitations of quasi-experimental designs and offer methods to improve them. We also perform a systematic review of four years of publications from two informatics journals to determine the number of quasi-experimental studies, classify these studies into their application domains, determine whether the potential limitations of quasi-experimental studies were acknowledged by the authors, and place these studies into the above-mentioned relative hierarchy.

The authors reviewed articles and book chapters on the design of quasi-experimental studies. 4 , 5 , 6 , 7 , 8 , 9 , 10 Most of the reviewed articles referenced two textbooks that were then reviewed in depth. 4 , 6

Key advantages and disadvantages of quasi-experimental studies, as they pertain to the study of medical informatics, were identified. The potential methodological flaws of quasi-experimental medical informatics studies, which have the potential to introduce bias, were also identified. In addition, a summary table outlining a relative hierarchy and nomenclature of quasi-experimental study designs is described. In general, the higher the design is in the hierarchy, the greater the internal validity that the study traditionally possesses because the evidence of the potential causation between the intervention and the outcome is strengthened. 4

We then performed a systematic review of four years of publications from two informatics journals. First, we determined the number of quasi-experimental studies. We then classified these studies on the above-mentioned hierarchy. We also classified the quasi-experimental studies according to their application domain. The categories of application domains employed were based on categorization used by Yearbooks of Medical Informatics 1992–2005 and were similar to the categories of application domains employed by Annual Symposiums of the American Medical Informatics Association. 11 The categories were (1) health and clinical management; (2) patient records; (3) health information systems; (4) medical signal processing and biomedical imaging; (5) decision support, knowledge representation, and management; (6) education and consumer informatics; and (7) bioinformatics. Because the quasi-experimental study design has recognized limitations, we sought to determine whether authors acknowledged the potential limitations of this design. Examples of acknowledgment included mention of lack of randomization, the potential for regression to the mean, the presence of temporal confounders and the mention of another design that would have more internal validity.

All original scientific manuscripts published between January 2000 and December 2003 in the Journal of the American Medical Informatics Association (JAMIA) and the International Journal of Medical Informatics (IJMI) were reviewed. One author (ADH) reviewed all the papers to identify the number of quasi-experimental studies. Other authors (ADH, JCM, JF) then independently reviewed all the studies identified as quasi-experimental. The three authors then convened as a group to resolve any disagreements in study classification, application domain, and acknowledgment of limitations.

Results and Discussion

What is a quasi-experiment.

Quasi-experiments are studies that aim to evaluate interventions but that do not use randomization. Similar to randomized trials, quasi-experiments aim to demonstrate causality between an intervention and an outcome. Quasi-experimental studies can use both preintervention and postintervention measurements as well as nonrandomly selected control groups.

Using this basic definition, it is evident that many published studies in medical informatics utilize the quasi-experimental design. Although the randomized controlled trial is generally considered to have the highest level of credibility with regard to assessing causality, in medical informatics, researchers often choose not to randomize the intervention for one or more reasons: (1) ethical considerations, (2) difficulty of randomizing subjects, (3) difficulty to randomize by locations (e.g., by wards), (4) small available sample size. Each of these reasons is discussed below.

Ethical considerations typically will not allow random withholding of an intervention with known efficacy. Thus, if the efficacy of an intervention has not been established, a randomized controlled trial is the design of choice to determine efficacy. But if the intervention under study incorporates an accepted, well-established therapeutic intervention, or if the intervention has either questionable efficacy or safety based on previously conducted studies, then the ethical issues of randomizing patients are sometimes raised. In the area of medical informatics, it is often believed prior to an implementation that an informatics intervention will likely be beneficial and thus medical informaticians and hospital administrators are often reluctant to randomize medical informatics interventions. In addition, there is often pressure to implement the intervention quickly because of its believed efficacy, thus not allowing researchers sufficient time to plan a randomized trial.

For medical informatics interventions, it is often difficult to randomize the intervention to individual patients or to individual informatics users. So while this randomization is technically possible, it is underused and thus compromises the eventual strength of concluding that an informatics intervention resulted in an outcome. For example, randomly allowing only half of medical residents to use pharmacy order-entry software at a tertiary care hospital is a scenario that hospital administrators and informatics users may not agree to for numerous reasons.

Similarly, informatics interventions often cannot be randomized to individual locations. Using the pharmacy order-entry system example, it may be difficult to randomize use of the system to only certain locations in a hospital or portions of certain locations. For example, if the pharmacy order-entry system involves an educational component, then people may apply the knowledge learned to nonintervention wards, thereby potentially masking the true effect of the intervention. When a design using randomized locations is employed successfully, the locations may be different in other respects (confounding variables), and this further complicates the analysis and interpretation.

In situations where it is known that only a small sample size will be available to test the efficacy of an intervention, randomization may not be a viable option. Randomization is beneficial because on average it tends to evenly distribute both known and unknown confounding variables between the intervention and control group. However, when the sample size is small, randomization may not adequately accomplish this balance. Thus, alternative design and analytical methods are often used in place of randomization when only small sample sizes are available.

What Are the Threats to Establishing Causality When Using Quasi-experimental Designs in Medical Informatics?

The lack of random assignment is the major weakness of the quasi-experimental study design. Associations identified in quasi-experiments meet one important requirement of causality since the intervention precedes the measurement of the outcome. Another requirement is that the outcome can be demonstrated to vary statistically with the intervention. Unfortunately, statistical association does not imply causality, especially if the study is poorly designed. Thus, in many quasi-experiments, one is most often left with the question: “Are there alternative explanations for the apparent causal association?” If these alternative explanations are credible, then the evidence of causation is less convincing. These rival hypotheses, or alternative explanations, arise from principles of epidemiologic study design.

Shadish et al. 4 outline nine threats to internal validity that are outlined in ▶ . Internal validity is defined as the degree to which observed changes in outcomes can be correctly inferred to be caused by an exposure or an intervention. In quasi-experimental studies of medical informatics, we believe that the methodological principles that most often result in alternative explanations for the apparent causal effect include (a) difficulty in measuring or controlling for important confounding variables, particularly unmeasured confounding variables, which can be viewed as a subset of the selection threat in ▶ ; (b) results being explained by the statistical principle of regression to the mean . Each of these latter two principles is discussed in turn.

Threats to Internal Validity

Adapted from Shadish et al. 4

An inability to sufficiently control for important confounding variables arises from the lack of randomization. A variable is a confounding variable if it is associated with the exposure of interest and is also associated with the outcome of interest; the confounding variable leads to a situation where a causal association between a given exposure and an outcome is observed as a result of the influence of the confounding variable. For example, in a study aiming to demonstrate that the introduction of a pharmacy order-entry system led to lower pharmacy costs, there are a number of important potential confounding variables (e.g., severity of illness of the patients, knowledge and experience of the software users, other changes in hospital policy) that may have differed in the preintervention and postintervention time periods ( ▶ ). In a multivariable regression, the first confounding variable could be addressed with severity of illness measures, but the second confounding variable would be difficult if not nearly impossible to measure and control. In addition, potential confounding variables that are unmeasured or immeasurable cannot be controlled for in nonrandomized quasi-experimental study designs and can only be properly controlled by the randomization process in randomized controlled trials.

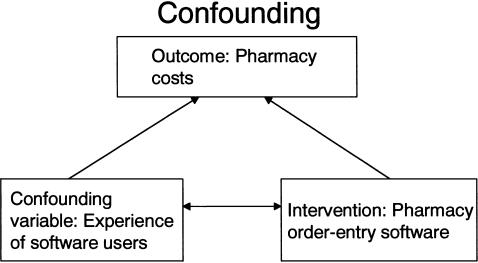
Example of confounding. To get the true effect of the intervention of interest, we need to control for the confounding variable.

Another important threat to establishing causality is regression to the mean. 12 , 13 , 14 This widespread statistical phenomenon can result in wrongly concluding that an effect is due to the intervention when in reality it is due to chance. The phenomenon was first described in 1886 by Francis Galton who measured the adult height of children and their parents. He noted that when the average height of the parents was greater than the mean of the population, the children tended to be shorter than their parents, and conversely, when the average height of the parents was shorter than the population mean, the children tended to be taller than their parents.

In medical informatics, what often triggers the development and implementation of an intervention is a rise in the rate above the mean or norm. For example, increasing pharmacy costs and adverse events may prompt hospital informatics personnel to design and implement pharmacy order-entry systems. If this rise in costs or adverse events is really just an extreme observation that is still within the normal range of the hospital's pharmaceutical costs (i.e., the mean pharmaceutical cost for the hospital has not shifted), then the statistical principle of regression to the mean predicts that these elevated rates will tend to decline even without intervention. However, often informatics personnel and hospital administrators cannot wait passively for this decline to occur. Therefore, hospital personnel often implement one or more interventions, and if a decline in the rate occurs, they may mistakenly conclude that the decline is causally related to the intervention. In fact, an alternative explanation for the finding could be regression to the mean.

What Are the Different Quasi-experimental Study Designs?

In the social sciences literature, quasi-experimental studies are divided into four study design groups 4 , 6 :

Quasi-experimental designs without control groups

Quasi-experimental designs that use control groups but no pretest

Quasi-experimental designs that use control groups and pretests

Interrupted time-series designs

There is a relative hierarchy within these categories of study designs, with category D studies being sounder than categories C, B, or A in terms of establishing causality. Thus, if feasible from a design and implementation point of view, investigators should aim to design studies that fall in to the higher rated categories. Shadish et al. 4 discuss 17 possible designs, with seven designs falling into category A, three designs in category B, and six designs in category C, and one major design in category D. In our review, we determined that most medical informatics quasi-experiments could be characterized by 11 of 17 designs, with six study designs in category A, one in category B, three designs in category C, and one design in category D because the other study designs were not used or feasible in the medical informatics literature. Thus, for simplicity, we have summarized the 11 study designs most relevant to medical informatics research in ▶ .

Relative Hierarchy of Quasi-experimental Designs

O = Observational Measurement; X = Intervention Under Study. Time moves from left to right.

In general, studies in category D are of higher study design quality than studies in category C, which are higher than those in category B, which are higher than those in category A. Also, as one moves down within each category, the studies become of higher quality, e.g., study 5 in category A is of higher study design quality than study 4, etc.

The nomenclature and relative hierarchy were used in the systematic review of four years of JAMIA and the IJMI. Similar to the relative hierarchy that exists in the evidence-based literature that assigns a hierarchy to randomized controlled trials, cohort studies, case-control studies, and case series, the hierarchy in ▶ is not absolute in that in some cases, it may be infeasible to perform a higher level study. For example, there may be instances where an A6 design established stronger causality than a B1 design. 15 , 16 , 17

Quasi-experimental Designs without Control Groups

Here, X is the intervention and O is the outcome variable (this notation is continued throughout the article). In this study design, an intervention (X) is implemented and a posttest observation (O1) is taken. For example, X could be the introduction of a pharmacy order-entry intervention and O1 could be the pharmacy costs following the intervention. This design is the weakest of the quasi-experimental designs that are discussed in this article. Without any pretest observations or a control group, there are multiple threats to internal validity. Unfortunately, this study design is often used in medical informatics when new software is introduced since it may be difficult to have pretest measurements due to time, technical, or cost constraints.

This is a commonly used study design. A single pretest measurement is taken (O1), an intervention (X) is implemented, and a posttest measurement is taken (O2). In this instance, period O1 frequently serves as the “control” period. For example, O1 could be pharmacy costs prior to the intervention, X could be the introduction of a pharmacy order-entry system, and O2 could be the pharmacy costs following the intervention. Including a pretest provides some information about what the pharmacy costs would have been had the intervention not occurred.

The advantage of this study design over A2 is that adding a second pretest prior to the intervention helps provide evidence that can be used to refute the phenomenon of regression to the mean and confounding as alternative explanations for any observed association between the intervention and the posttest outcome. For example, in a study where a pharmacy order-entry system led to lower pharmacy costs (O3 < O2 and O1), if one had two preintervention measurements of pharmacy costs (O1 and O2) and they were both elevated, this would suggest that there was a decreased likelihood that O3 is lower due to confounding and regression to the mean. Similarly, extending this study design by increasing the number of measurements postintervention could also help to provide evidence against confounding and regression to the mean as alternate explanations for observed associations.

This design involves the inclusion of a nonequivalent dependent variable ( b ) in addition to the primary dependent variable ( a ). Variables a and b should assess similar constructs; that is, the two measures should be affected by similar factors and confounding variables except for the effect of the intervention. Variable a is expected to change because of the intervention X, whereas variable b is not. Taking our example, variable a could be pharmacy costs and variable b could be the length of stay of patients. If our informatics intervention is aimed at decreasing pharmacy costs, we would expect to observe a decrease in pharmacy costs but not in the average length of stay of patients. However, a number of important confounding variables, such as severity of illness and knowledge of software users, might affect both outcome measures. Thus, if the average length of stay did not change following the intervention but pharmacy costs did, then the data are more convincing than if just pharmacy costs were measured.

The Removed-Treatment Design

This design adds a third posttest measurement (O3) to the one-group pretest-posttest design and then removes the intervention before a final measure (O4) is made. The advantage of this design is that it allows one to test hypotheses about the outcome in the presence of the intervention and in the absence of the intervention. Thus, if one predicts a decrease in the outcome between O1 and O2 (after implementation of the intervention), then one would predict an increase in the outcome between O3 and O4 (after removal of the intervention). One caveat is that if the intervention is thought to have persistent effects, then O4 needs to be measured after these effects are likely to have disappeared. For example, a study would be more convincing if it demonstrated that pharmacy costs decreased after pharmacy order-entry system introduction (O2 and O3 less than O1) and that when the order-entry system was removed or disabled, the costs increased (O4 greater than O2 and O3 and closer to O1). In addition, there are often ethical issues in this design in terms of removing an intervention that may be providing benefit.

The Repeated-Treatment Design

The advantage of this design is that it demonstrates reproducibility of the association between the intervention and the outcome. For example, the association is more likely to be causal if one demonstrates that a pharmacy order-entry system results in decreased pharmacy costs when it is first introduced and again when it is reintroduced following an interruption of the intervention. As for design A5, the assumption must be made that the effect of the intervention is transient, which is most often applicable to medical informatics interventions. Because in this design, subjects may serve as their own controls, this may yield greater statistical efficiency with fewer numbers of subjects.

Quasi-experimental Designs That Use a Control Group but No Pretest

An intervention X is implemented for one group and compared to a second group. The use of a comparison group helps prevent certain threats to validity including the ability to statistically adjust for confounding variables. Because in this study design, the two groups may not be equivalent (assignment to the groups is not by randomization), confounding may exist. For example, suppose that a pharmacy order-entry intervention was instituted in the medical intensive care unit (MICU) and not the surgical intensive care unit (SICU). O1 would be pharmacy costs in the MICU after the intervention and O2 would be pharmacy costs in the SICU after the intervention. The absence of a pretest makes it difficult to know whether a change has occurred in the MICU. Also, the absence of pretest measurements comparing the SICU to the MICU makes it difficult to know whether differences in O1 and O2 are due to the intervention or due to other differences in the two units (confounding variables).

Quasi-experimental Designs That Use Control Groups and Pretests

The reader should note that with all the studies in this category, the intervention is not randomized. The control groups chosen are comparison groups. Obtaining pretest measurements on both the intervention and control groups allows one to assess the initial comparability of the groups. The assumption is that if the intervention and the control groups are similar at the pretest, the smaller the likelihood there is of important confounding variables differing between the two groups.

The use of both a pretest and a comparison group makes it easier to avoid certain threats to validity. However, because the two groups are nonequivalent (assignment to the groups is not by randomization), selection bias may exist. Selection bias exists when selection results in differences in unit characteristics between conditions that may be related to outcome differences. For example, suppose that a pharmacy order-entry intervention was instituted in the MICU and not the SICU. If preintervention pharmacy costs in the MICU (O1a) and SICU (O1b) are similar, it suggests that it is less likely that there are differences in the important confounding variables between the two units. If MICU postintervention costs (O2a) are less than preintervention MICU costs (O1a), but SICU costs (O1b) and (O2b) are similar, this suggests that the observed outcome may be causally related to the intervention.

In this design, the pretests are administered at two different times. The main advantage of this design is that it controls for potentially different time-varying confounding effects in the intervention group and the comparison group. In our example, measuring points O1 and O2 would allow for the assessment of time-dependent changes in pharmacy costs, e.g., due to differences in experience of residents, preintervention between the intervention and control group, and whether these changes were similar or different.

With this study design, the researcher administers an intervention at a later time to a group that initially served as a nonintervention control. The advantage of this design over design C2 is that it demonstrates reproducibility in two different settings. This study design is not limited to two groups; in fact, the study results have greater validity if the intervention effect is replicated in different groups at multiple times. In the example of a pharmacy order-entry system, one could implement or intervene in the MICU and then at a later time, intervene in the SICU. This latter design is often very applicable to medical informatics where new technology and new software is often introduced or made available gradually.

Interrupted Time-Series Designs

An interrupted time-series design is one in which a string of consecutive observations equally spaced in time is interrupted by the imposition of a treatment or intervention. The advantage of this design is that with multiple measurements both pre- and postintervention, it is easier to address and control for confounding and regression to the mean. In addition, statistically, there is a more robust analytic capability, and there is the ability to detect changes in the slope or intercept as a result of the intervention in addition to a change in the mean values. 18 A change in intercept could represent an immediate effect while a change in slope could represent a gradual effect of the intervention on the outcome. In the example of a pharmacy order-entry system, O1 through O5 could represent monthly pharmacy costs preintervention and O6 through O10 monthly pharmacy costs post the introduction of the pharmacy order-entry system. Interrupted time-series designs also can be further strengthened by incorporating many of the design features previously mentioned in other categories (such as removal of the treatment, inclusion of a nondependent outcome variable, or the addition of a control group).

Systematic Review Results

The results of the systematic review are in ▶ . In the four-year period of JAMIA publications that the authors reviewed, 25 quasi-experimental studies among 22 articles were published. Of these 25, 15 studies were of category A, five studies were of category B, two studies were of category C, and no studies were of category D. Although there were no studies of category D (interrupted time-series analyses), three of the studies classified as category A had data collected that could have been analyzed as an interrupted time-series analysis. Nine of the 25 studies (36%) mentioned at least one of the potential limitations of the quasi-experimental study design. In the four-year period of IJMI publications reviewed by the authors, nine quasi-experimental studies among eight manuscripts were published. Of these nine, five studies were of category A, one of category B, one of category C, and two of category D. Two of the nine studies (22%) mentioned at least one of the potential limitations of the quasi-experimental study design.

Systematic Review of Four Years of Quasi-designs in JAMIA

JAMIA = Journal of the American Medical Informatics Association; IJMI = International Journal of Medical Informatics.

Could have been analyzed as an interrupted time-series design.

In addition, three studies from JAMIA were based on a counterbalanced design. A counterbalanced design is a higher order study design than other studies in category A. The counterbalanced design is sometimes referred to as a Latin-square arrangement. In this design, all subjects receive all the different interventions but the order of intervention assignment is not random. 19 This design can only be used when the intervention is compared against some existing standard, for example, if a new PDA-based order entry system is to be compared to a computer terminal–based order entry system. In this design, all subjects receive the new PDA-based order entry system and the old computer terminal-based order entry system. The counterbalanced design is a within-participants design, where the order of the intervention is varied (e.g., one group is given software A followed by software B and another group is given software B followed by software A). The counterbalanced design is typically used when the available sample size is small, thus preventing the use of randomization. This design also allows investigators to study the potential effect of ordering of the informatics intervention.

Although quasi-experimental study designs are ubiquitous in the medical informatics literature, as evidenced by 34 studies in the past four years of the two informatics journals, little has been written about the benefits and limitations of the quasi-experimental approach. As we have outlined in this paper, a relative hierarchy and nomenclature of quasi-experimental study designs exist, with some designs being more likely than others to permit causal interpretations of observed associations. Strengths and limitations of a particular study design should be discussed when presenting data collected in the setting of a quasi-experimental study. Future medical informatics investigators should choose the strongest design that is feasible given the particular circumstances.

Supplementary Material

Dr. Harris was supported by NIH grants K23 AI01752-01A1 and R01 AI60859-01A1. Dr. Perencevich was supported by a VA Health Services Research and Development Service (HSR&D) Research Career Development Award (RCD-02026-1). Dr. Finkelstein was supported by NIH grant RO1 HL71690.

• 1. Rothman KJ, Greenland S. Modern epidemiology. Philadelphia: Lippincott–Raven Publishers, 1998.
• 2. Hennekens CH, Buring JE. Epidemiology in medicine. Boston: Little, Brown, 1987.
• 3. Szklo M, Nieto FJ. Epidemiology: beyond the basics. Gaithersburg, MD: Aspen Publishers, 2000.
• 4. Shadish WR, Cook TD, Campbell DT. Experimental and quasi-experimental designs for generalized causal inference. Boston: Houghton Mifflin, 2002.
• 5. Trochim WMK. The research methods knowledge base. Cincinnati: Atomic Dog Publishing, 2001.
• 6. Cook TD, Campbell DT. Quasi-experimentation: design and analysis issues for field settings. Chicago: Rand McNally Publishing Company, 1979.
• 7. MacLehose RR, Reeves BC, Harvey IM, Sheldon TA, Russell IT, Black AM. A systematic review of comparisons of effect sizes derived from randomised and non-randomised studies. Health Technol Assess. 2000;4:1–154. [ PubMed ] [ Google Scholar ]
• 8. Shadish WR, Heinsman DT. Experiments versus quasi-experiments: do they yield the same answer? NIDA Res Monogr. 1997;170:147–64. [ PubMed ] [ Google Scholar ]
• 9. Grimshaw J, Campbell M, Eccles M, Steen N. Experimental and quasi-experimental designs for evaluating guideline implementation strategies. Fam Pract. 2000;17(Suppl 1):S11–6. [ DOI ] [ PubMed ] [ Google Scholar ]
• 10. Zwerling C, Daltroy LH, Fine LJ, Johnston JJ, Melius J, Silverstein BA. Design and conduct of occupational injury intervention studies: a review of evaluation strategies. Am J Ind Med. 1997;32:164–79. [ DOI ] [ PubMed ] [ Google Scholar ]
• 11. Haux RKC, editor. Yearbook of medical informatics 2005. Stuttgart: Schattauer Verlagsgesellschaft, 2005, 563.
• 12. Morton V, Torgerson DJ. Effect of regression to the mean on decision making in health care. BMJ. 2003;326:1083–4. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 13. Bland JM, Altman DG. Regression towards the mean. BMJ. 1994;308:1499. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 14. Bland JM, Altman DG. Some examples of regression towards the mean. BMJ. 1994;309:780. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 15. Guyatt GH, Haynes RB, Jaeschke RZ, Cook DJ, Green L, Naylor CD, et al. Users' guides to the medical literature: XXV. Evidence-based medicine: principles for applying the users' guides to patient care. Evidence-Based Medicine Working Group. JAMA. 2000;284:1290–6. [ DOI ] [ PubMed ] [ Google Scholar ]
• 16. Harris RP, Helfand M, Woolf SH, Lohr KN, Mulrow CD, Teutsch SM, et al. Current methods of the US Preventive Services Task Force: a review of the process. Am J Prev Med. 2001;20:21–35. [ DOI ] [ PubMed ] [ Google Scholar ]
• 17. Harbour R, Miller J. A new system for grading recommendations in evidence based guidelines. BMJ. 2001;323:334–6. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 18. Wagner AK, Soumerai SB, Zhang F, Ross-Degnan D. Segmented regression analysis of interrupted time series studies in medication use research. J Clin Pharm Ther. 2002;27:299–309. [ DOI ] [ PubMed ] [ Google Scholar ]
• 19. Campbell DT. Counterbalanced design. In: Company RMCP, editor. Experimental and Quasiexperimental Designs for Research. Chicago: Rand-McNally College Publishing Company, 1963, 50–5.
• 20. Staggers N, Kobus D. Comparing response time, errors, and satisfaction between text-based and graphical user interfaces during nursing order tasks. J Am Med Inform Assoc. 2000;7:164–76. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 21. Schriger DL, Baraff LJ, Buller K, Shendrikar MA, Nagda S, Lin EJ, et al. Implementation of clinical guidelines via a computer charting system: effect on the care of febrile children less than three years of age. J Am Med Inform Assoc. 2000;7:186–95. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 22. Patel VL, Kushniruk AW, Yang S, Yale JF. Impact of a computer-based patient record system on data collection, knowledge organization, and reasoning. J Am Med Inform Assoc. 2000;7:569–85. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 23. Borowitz SM. Computer-based speech recognition as an alternative to medical transcription. J Am Med Inform Assoc. 2001;8:101–2. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 24. Patterson R, Harasym P. Educational instruction on a hospital information system for medical students during their surgical rotations. J Am Med Inform Assoc. 2001;8:111–6. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 25. Rocha BH, Christenson JC, Evans RS, Gardner RM. Clinicians' response to computerized detection of infections. J Am Med Inform Assoc. 2001;8:117–25. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 26. Lovis C, Chapko MK, Martin DP, Payne TH, Baud RH, Hoey PJ, et al. Evaluation of a command-line parser-based order entry pathway for the Department of Veterans Affairs electronic patient record. J Am Med Inform Assoc. 2001;8:486–98. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 27. Hersh WR, Junium K, Mailhot M, Tidmarsh P. Implementation and evaluation of a medical informatics distance education program. J Am Med Inform Assoc. 2001;8:570–84. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 28. Makoul G, Curry RH, Tang PC. The use of electronic medical records: communication patterns in outpatient encounters. J Am Med Inform Assoc. 2001;8:610–5. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 29. Ruland CM. Handheld technology to improve patient care: evaluating a support system for preference-based care planning at the bedside. J Am Med Inform Assoc. 2002;9:192–201. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 30. De Lusignan S, Stephens PN, Adal N, Majeed A. Does feedback improve the quality of computerized medical records in primary care? J Am Med Inform Assoc. 2002;9:395–401. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 31. Mekhjian HS, Kumar RR, Kuehn L, Bentley TD, Teater P, Thomas A, et al. Immediate benefits realized following implementation of physician order entry at an academic medical center. J Am Med Inform Assoc. 2002;9:529–39. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 32. Ammenwerth E, Mansmann U, Iller C, Eichstadter R. Factors affecting and affected by user acceptance of computer-based nursing documentation: results of a two-year study. J Am Med Inform Assoc. 2003;10:69–84. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 33. Oniki TA, Clemmer TP, Pryor TA. The effect of computer-generated reminders on charting deficiencies in the ICU. J Am Med Inform Assoc. 2003;10:177–87. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 34. Liederman EM, Morefield CS. Web messaging: a new tool for patient-physician communication. J Am Med Inform Assoc. 2003;10:260–70. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 35. Rotich JK, Hannan TJ, Smith FE, Bii J, Odero WW, Vu N, Mamlin BW, et al. Installing and implementing a computer-based patient record system in sub-Saharan Africa: the Mosoriot Medical Record System. J Am Med Inform Assoc. 2003;10:295–303. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 36. Payne TH, Hoey PJ, Nichol P, Lovis C. Preparation and use of preconstructed orders, order sets, and order menus in a computerized provider order entry system. J Am Med Inform Assoc. 2003;10:322–9. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 37. Hoch I, Heymann AD, Kurman I, Valinsky LJ, Chodick G, Shalev V. Countrywide computer alerts to community physicians improve potassium testing in patients receiving diuretics. J Am Med Inform Assoc. 2003;10:541–6. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 38. Laerum H, Karlsen TH, Faxvaag A. Effects of scanning and eliminating paper-based medical records on hospital physicians' clinical work practice. J Am Med Inform Assoc. 2003;10:588–95. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 39. Devine EG, Gaehde SA, Curtis AC. Comparative evaluation of three continuous speech recognition software packages in the generation of medical reports. J Am Med Inform Assoc. 2000;7:462–8. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 40. Dunbar PJ, Madigan D, Grohskopf LA, Revere D, Woodward J, Minstrell J, et al. A two-way messaging system to enhance antiretroviral adherence. J Am Med Inform Assoc. 2003;10:11–5. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 41. Lenert L, Munoz RF, Stoddard J, Delucchi K, Bansod A, Skoczen S, et al. Design and pilot evaluation of an Internet smoking cessation program. J Am Med Inform Assoc. 2003;10:16–20. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 42. Koide D, Ohe K, Ross-Degnan D, Kaihara S. Computerized reminders to monitor liver function to improve the use of etretinate. Int J Med Inf. 2000;57:11–9. [ DOI ] [ PubMed ] [ Google Scholar ]
• 43. Gonzalez-Heydrich J, DeMaso DR, Irwin C, Steingard RJ, Kohane IS, Beardslee WR. Implementation of an electronic medical record system in a pediatric psychopharmacology program. Int J Med Inf. 2000;57:109–16. [ DOI ] [ PubMed ] [ Google Scholar ]
• 44. Anantharaman V, Swee Han L. Hospital and emergency ambulance link: using IT to enhance emergency pre-hospital care. Int J Med Inf. 2001;61:147–61. [ DOI ] [ PubMed ] [ Google Scholar ]
• 45. Chae YM, Heon Lee J, Hee Ho S, Ja Kim H, Hong Jun K, Uk Won J. Patient satisfaction with telemedicine in home health services for the elderly. Int J Med Inf. 2001;61:167–73. [ DOI ] [ PubMed ] [ Google Scholar ]
• 46. Lin CC, Chen HS, Chen CY, Hou SM. Implementation and evaluation of a multifunctional telemedicine system in NTUH. Int J Med Inf. 2001;61:175–87. [ DOI ] [ PubMed ] [ Google Scholar ]
• 47. Mikulich VJ, Liu YC, Steinfeldt J, Schriger DL. Implementation of clinical guidelines through an electronic medical record: physician usage, satisfaction and assessment. Int J Med Inf. 2001;63:169–78. [ DOI ] [ PubMed ] [ Google Scholar ]
• 48. Hwang JI, Park HA, Bakken S. Impact of a physician's order entry (POE) system on physicians' ordering patterns and patient length of stay. Int J Med Inf. 2002;65:213–23. [ DOI ] [ PubMed ] [ Google Scholar ]
• 49. Park WS, Kim JS, Chae YM, Yu SH, Kim CY, Kim SA, et al. Does the physician order-entry system increase the revenue of a general hospital? Int J Med Inf. 2003;71:25–32. [ DOI ] [ PubMed ] [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

• View on publisher site
• PDF (115.2 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

educational research techniques

Research techniques and education.

Experimental Designs: Between Groups

In experimental research, there are two common designs. They are between and within group design. The difference between these two groups of designs is that between group involves two or more groups in an experiment while within group involves only one group.

This post will focus on between group designs. We will look at the following forms of between group design…

• True/quasi-experiment
• Factorial Design

True/quasi Experiment

A true experiment is one in which the participants are randomly assigned to different groups. In a quasi-experiment, the researcher is not able to randomly assigned participants to different groups.

Whether the experiment is a true experiment or a quasi-experiment. There are always two groups that are compared in the study. One group is the controlled group, which does not receive the treatment. The other group is called the experimental group, which receives the treatment of the study. It is possible to have more than two groups and several treatments but the minimum for between group designs is two groups.

Another characteristic that true and quasi-experiments have in common is the type of formats that the experiment can take. There are two common formats

• Pre- and post test
• Post test only

A pre- and post test involves measuring the groups of the study before the treatment and after the treatment. The desire normally is for the groups to be the same before the treatment and for them to be different statistically after the treatment. The reason for them being different is because of the treatment, at least hopefully.

For example, let’s say you have some bushes and you want to see if the fertilizer you bought makes any difference in the growth of the bushes.  You divide the bushes into two groups, one that receives the fertilizer (experimental group), and one that does not (controlled group). You measure the height of the bushes before the experiment to be sure they are the same. Then, you apply the fertilizer to the experimental group and after a period of time, you measure the heights of both groups again. If the fertilized bushes grow taller than the control group you can infer that it is because of the fertilizer.

Post-test only design is when the groups are measured only after the treatment. For example, let’s say you have some corn plants and you want to see if the fertilizer you bought makes any difference.in the amount of corn produced.  You divide the corn plants into two groups, one that receives the fertilizer (experimental group), and one that does not (controlled group). You apply the fertilizer to the control group and after a period of time, you measure the amount of corn produced. If the fertilized corn produces more you can infer that it is because of the fertilizer. You never measure the corn beforehand because they had not produced any corn yet.

Factorial design involves the use of more than one treatment. Returning to the corn example, let’s say you want to see not only how fertilizer affects corn production but also how the amount of water the corn receives affects production as well.

In this example, you are trying to see if there is an interaction effect between fertilizer and water.  When water and fertilizer are increased does production increase, is there no increase, or if one goes up and the other goes down does that have an effect?

Between group designs such as true and quasi-experiments provide a way for researchers to establish cause and effect. Pre- post test is employed as well as factorial designs to establish relationships between variables

Share this:

2 thoughts on “ experimental designs: between groups ”.

Pingback: Experimental Design: Within Groups | educationalresearchtechniques

Pingback: Experimental Designs: Between Groups | Educatio...

Leave a Reply Cancel reply

Discover more from educational research techniques.

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

Quasi-Experimental Design: Definition, Types, Examples

Appinio Research · 19.12.2023 · 37min read

Ever wondered how researchers uncover cause-and-effect relationships in the real world, where controlled experiments are often elusive? Quasi-experimental design holds the key. In this guide, we'll unravel the intricacies of quasi-experimental design, shedding light on its definition, purpose, and applications across various domains. Whether you're a student, a professional, or simply curious about the methods behind meaningful research, join us as we delve into the world of quasi-experimental design, making complex concepts sound simple and embarking on a journey of knowledge and discovery.

What is Quasi-Experimental Design?

Quasi-experimental design is a research methodology used to study the effects of independent variables on dependent variables when full experimental control is not possible or ethical. It falls between controlled experiments, where variables are tightly controlled, and purely observational studies, where researchers have little control over variables. Quasi-experimental design mimics some aspects of experimental research but lacks randomization.

The primary purpose of quasi-experimental design is to investigate cause-and-effect relationships between variables in real-world settings. Researchers use this approach to answer research questions, test hypotheses, and explore the impact of interventions or treatments when they cannot employ traditional experimental methods. Quasi-experimental studies aim to maximize internal validity and make meaningful inferences while acknowledging practical constraints and ethical considerations.

Quasi-Experimental vs. Experimental Design

It's essential to understand the distinctions between Quasi-Experimental and Experimental Design to appreciate the unique characteristics of each approach:

• Randomization:  In Experimental Design, random assignment of participants to groups is a defining feature. Quasi-experimental design, on the other hand, lacks randomization due to practical constraints or ethical considerations.
• Control Groups :  Experimental Design typically includes control groups that are subjected to no treatment or a placebo. The quasi-experimental design may have comparison groups but lacks the same level of control.
• Manipulation of IV:  Experimental Design involves the intentional manipulation of the independent variable. Quasi-experimental design often deals with naturally occurring independent variables.
• Causal Inference:  Experimental Design allows for stronger causal inferences due to randomization and control. Quasi-experimental design permits causal inferences but with some limitations.

When to Use Quasi-Experimental Design?

A quasi-experimental design is particularly valuable in several situations:

• Ethical Constraints:  When manipulating the independent variable is ethically unacceptable or impractical, quasi-experimental design offers an alternative to studying naturally occurring variables.
• Real-World Settings:  When researchers want to study phenomena in real-world contexts, quasi-experimental design allows them to do so without artificial laboratory settings.
• Limited Resources:  In cases where resources are limited and conducting a controlled experiment is cost-prohibitive, quasi-experimental design can provide valuable insights.
• Policy and Program Evaluation:  Quasi-experimental design is commonly used in evaluating the effectiveness of policies, interventions, or programs that cannot be randomly assigned to participants.

Importance of Quasi-Experimental Design in Research

Quasi-experimental design plays a vital role in research for several reasons:

• Addressing Real-World Complexities:  It allows researchers to tackle complex real-world issues where controlled experiments are not feasible. This bridges the gap between controlled experiments and purely observational studies.
• Ethical Research:  It provides an honest approach when manipulating variables or assigning treatments could harm participants or violate ethical standards.
• Policy and Practice Implications:  Quasi-experimental studies generate findings with direct applications in policy-making and practical solutions in fields such as education, healthcare, and social sciences.
• Enhanced External Validity:  Findings from Quasi-Experimental research often have high external validity, making them more applicable to broader populations and contexts.

By embracing the challenges and opportunities of quasi-experimental design, researchers can contribute valuable insights to their respective fields and drive positive changes in the real world.

Key Concepts in Quasi-Experimental Design

In quasi-experimental design, it's essential to grasp the fundamental concepts underpinning this research methodology. Let's explore these key concepts in detail.

Independent Variable

The independent variable (IV) is the factor you aim to study or manipulate in your research. Unlike controlled experiments, where you can directly manipulate the IV, quasi-experimental design often deals with naturally occurring variables. For example, if you're investigating the impact of a new teaching method on student performance, the teaching method is your independent variable.

Dependent Variable

The dependent variable (DV) is the outcome or response you measure to assess the effects of changes in the independent variable. Continuing with the teaching method example, the dependent variable would be the students' academic performance, typically measured using test scores, grades, or other relevant metrics.

Control Groups vs. Comparison Groups

While quasi-experimental design lacks the luxury of randomly assigning participants to control and experimental groups, you can still establish comparison groups to make meaningful inferences. Control groups consist of individuals who do not receive the treatment, while comparison groups are exposed to different levels or variations of the treatment. These groups help researchers gauge the effect of the independent variable.

Pre-Test and Post-Test Measures

In quasi-experimental design, it's common practice to collect data both before and after implementing the independent variable. The initial data (pre-test) serves as a baseline, allowing you to measure changes over time (post-test). This approach helps assess the impact of the independent variable more accurately. For instance, if you're studying the effectiveness of a new drug, you'd measure patients' health before administering the drug (pre-test) and afterward (post-test).

Threats to Internal Validity

Internal validity is crucial for establishing a cause-and-effect relationship between the independent and dependent variables. However, in a quasi-experimental design, several threats can compromise internal validity. These threats include:

• Selection Bias :  When non-randomized groups differ systematically in ways that affect the study's outcome.
• History Effects:  External events or changes over time that influence the results.
• Maturation Effects:  Natural changes or developments that occur within participants during the study.
• Regression to the Mean:  The tendency for extreme scores on a variable to move closer to the mean upon retesting.
• Attrition and Mortality:  The loss of participants over time, potentially skewing the results.
• Testing Effects:  The mere act of testing or assessing participants can impact their subsequent performance.

Understanding these threats is essential for designing and conducting Quasi-Experimental studies that yield valid and reliable results.

Randomization and Non-Randomization

In traditional experimental designs, randomization is a powerful tool for ensuring that groups are equivalent at the outset of a study. However, quasi-experimental design often involves non-randomization due to the nature of the research. This means that participants are not randomly assigned to treatment and control groups. Instead, researchers must employ various techniques to minimize biases and ensure that the groups are as similar as possible.

For example, if you are conducting a study on the effects of a new teaching method in a real classroom setting, you cannot randomly assign students to the treatment and control groups. Instead, you might use statistical methods to match students based on relevant characteristics such as prior academic performance or socioeconomic status. This matching process helps control for potential confounding variables, increasing the validity of your study.

Types of Quasi-Experimental Designs

In quasi-experimental design, researchers employ various approaches to investigate causal relationships and study the effects of independent variables when complete experimental control is challenging. Let's explore these types of quasi-experimental designs.

One-Group Posttest-Only Design

The One-Group Posttest-Only Design is one of the simplest forms of quasi-experimental design. In this design, a single group is exposed to the independent variable, and data is collected only after the intervention has taken place. Unlike controlled experiments, there is no comparison group. This design is useful when researchers cannot administer a pre-test or when it is logistically difficult to do so.

Example : Suppose you want to assess the effectiveness of a new time management seminar. You offer the seminar to a group of employees and measure their productivity levels immediately afterward to determine if there's an observable impact.

One-Group Pretest-Posttest Design

Similar to the One-Group Posttest-Only Design, this approach includes a pre-test measure in addition to the post-test. Researchers collect data both before and after the intervention. By comparing the pre-test and post-test results within the same group, you can gain a better understanding of the changes that occur due to the independent variable.

Example : If you're studying the impact of a stress management program on participants' stress levels, you would measure their stress levels before the program (pre-test) and after completing the program (post-test) to assess any changes.

Non-Equivalent Groups Design

The Non-Equivalent Groups Design involves multiple groups, but they are not randomly assigned. Instead, researchers must carefully match or control for relevant variables to minimize biases. This design is particularly useful when random assignment is not possible or ethical.

Example : Imagine you're examining the effectiveness of two teaching methods in two different schools. You can't randomly assign students to the schools, but you can carefully match them based on factors like age, prior academic performance, and socioeconomic status to create equivalent groups.

Time Series Design

Time Series Design is an approach where data is collected at multiple time points before and after the intervention. This design allows researchers to analyze trends and patterns over time, providing valuable insights into the sustained effects of the independent variable.

Example : If you're studying the impact of a new marketing campaign on product sales, you would collect sales data at regular intervals (e.g., monthly) before and after the campaign's launch to observe any long-term trends.

Regression Discontinuity Design

Regression Discontinuity Design is employed when participants are assigned to different groups based on a specific cutoff score or threshold. This design is often used in educational and policy research to assess the effects of interventions near a cutoff point.

Example : Suppose you're evaluating the impact of a scholarship program on students' academic performance. Students who score just above or below a certain GPA threshold are assigned differently to the program. This design helps assess the program's effectiveness at the cutoff point.

Propensity Score Matching

Propensity Score Matching is a technique used to create comparable treatment and control groups in non-randomized studies. Researchers calculate propensity scores based on participants' characteristics and match individuals in the treatment group to those in the control group with similar scores.

Example : If you're studying the effects of a new medication on patient outcomes, you would use propensity scores to match patients who received the medication with those who did not but have similar health profiles.

Interrupted Time Series Design

The Interrupted Time Series Design involves collecting data at multiple time points before and after the introduction of an intervention. However, in this design, the intervention occurs at a specific point in time, allowing researchers to assess its immediate impact.

Example : Let's say you're analyzing the effects of a new traffic management system on traffic accidents. You collect accident data before and after the system's implementation to observe any abrupt changes right after its introduction.

Each of these quasi-experimental designs offers unique advantages and is best suited to specific research questions and scenarios. Choosing the right design is crucial for conducting robust and informative studies.

Advantages and Disadvantages of Quasi-Experimental Design

Quasi-experimental design offers a valuable research approach, but like any methodology, it comes with its own set of advantages and disadvantages. Let's explore these in detail.

Quasi-Experimental Design Advantages

Quasi-experimental design presents several advantages that make it a valuable tool in research:

• Real-World Applicability:  Quasi-experimental studies often take place in real-world settings, making the findings more applicable to practical situations. Researchers can examine the effects of interventions or variables in the context where they naturally occur.
• Ethical Considerations:  In situations where manipulating the independent variable in a controlled experiment would be unethical, quasi-experimental design provides an ethical alternative. For example, it would be unethical to assign participants to smoke for a study on the health effects of smoking, but you can study naturally occurring groups of smokers and non-smokers.
• Cost-Efficiency:  Conducting Quasi-Experimental research is often more cost-effective than conducting controlled experiments. The absence of controlled environments and extensive manipulations can save both time and resources.

These advantages make quasi-experimental design an attractive choice for researchers facing practical or ethical constraints in their studies.

Quasi-Experimental Design Disadvantages

However, quasi-experimental design also comes with its share of challenges and disadvantages:

• Limited Control:  Unlike controlled experiments, where researchers have full control over variables, quasi-experimental design lacks the same level of control. This limited control can result in confounding variables that make it difficult to establish causality.
• Threats to Internal Validity:  Various threats to internal validity, such as selection bias, history effects, and maturation effects, can compromise the accuracy of causal inferences. Researchers must carefully address these threats to ensure the validity of their findings.
• Causality Inference Challenges:  Establishing causality can be challenging in quasi-experimental design due to the absence of randomization and control. While you can make strong arguments for causality, it may not be as conclusive as in controlled experiments.
• Potential Confounding Variables:  In a quasi-experimental design, it's often challenging to control for all possible confounding variables that may affect the dependent variable. This can lead to uncertainty in attributing changes solely to the independent variable.

Despite these disadvantages, quasi-experimental design remains a valuable research tool when used judiciously and with a keen awareness of its limitations. Researchers should carefully consider their research questions and the practical constraints they face before choosing this approach.

How to Conduct a Quasi-Experimental Study?

Conducting a Quasi-Experimental study requires careful planning and execution to ensure the validity of your research. Let's dive into the essential steps you need to follow when conducting such a study.

1. Define Research Questions and Objectives

The first step in any research endeavor is clearly defining your research questions and objectives. This involves identifying the independent variable (IV) and the dependent variable (DV) you want to study. What is the specific relationship you want to explore, and what do you aim to achieve with your research?

• Specify Your Research Questions :  Start by formulating precise research questions that your study aims to answer. These questions should be clear, focused, and relevant to your field of study.
• Identify the Independent Variable:  Define the variable you intend to manipulate or study in your research. Understand its significance in your study's context.
• Determine the Dependent Variable:  Identify the outcome or response variable that will be affected by changes in the independent variable.
• Establish Hypotheses (If Applicable):  If you have specific hypotheses about the relationship between the IV and DV, state them clearly. Hypotheses provide a framework for testing your research questions.

2. Select the Appropriate Quasi-Experimental Design

Choosing the right quasi-experimental design is crucial for achieving your research objectives. Select a design that aligns with your research questions and the available data. Consider factors such as the feasibility of implementing the design and the ethical considerations involved.

• Evaluate Your Research Goals:  Assess your research questions and objectives to determine which type of quasi-experimental design is most suitable. Each design has its strengths and limitations, so choose one that aligns with your goals.
• Consider Ethical Constraints:  Take into account any ethical concerns related to your research. Depending on your study's context, some designs may be more ethically sound than others.
• Assess Data Availability:  Ensure you have access to the necessary data for your chosen design. Some designs may require extensive historical data, while others may rely on data collected during the study.

3. Identify and Recruit Participants

Selecting the right participants is a critical aspect of Quasi-Experimental research. The participants should represent the population you want to make inferences about, and you must address ethical considerations, including informed consent.

• Define Your Target Population:  Determine the population that your study aims to generalize to. Your sample should be representative of this population.
• Recruitment Process:  Develop a plan for recruiting participants. Depending on your design, you may need to reach out to specific groups or institutions.
• Informed Consent:  Ensure that you obtain informed consent from participants. Clearly explain the nature of the study, potential risks, and their rights as participants.

4. Collect Data

Data collection is a crucial step in Quasi-Experimental research. You must adhere to a consistent and systematic process to gather relevant information before and after the intervention or treatment.

• Pre-Test Measures:  If applicable, collect data before introducing the independent variable. Ensure that the pre-test measures are standardized and reliable.
• Post-Test Measures:  After the intervention, collect post-test data using the same measures as the pre-test. This allows you to assess changes over time.
• Maintain Data Consistency:  Ensure that data collection procedures are consistent across all participants and time points to minimize biases.

5. Analyze Data

Once you've collected your data, it's time to analyze it using appropriate statistical techniques . The choice of analysis depends on your research questions and the type of data you've gathered.

• Statistical Analysis :  Use statistical software to analyze your data. Common techniques include t-tests , analysis of variance (ANOVA) , regression analysis , and more, depending on the design and variables.
• Control for Confounding Variables:  Be aware of potential confounding variables and include them in your analysis as covariates to ensure accurate results.

Chi-Square Calculator :

t-Test Calculator :

6. Interpret Results

With the analysis complete, you can interpret the results to draw meaningful conclusions about the relationship between the independent and dependent variables.

• Examine Effect Sizes:  Assess the magnitude of the observed effects to determine their practical significance.
• Consider Significance Levels:  Determine whether the observed results are statistically significant . Understand the p-values and their implications.
• Compare Findings to Hypotheses:  Evaluate whether your findings support or reject your hypotheses and research questions.

7. Draw Conclusions

Based on your analysis and interpretation of the results, draw conclusions about the research questions and objectives you set out to address.

• Causal Inferences:  Discuss the extent to which your study allows for causal inferences. Be transparent about the limitations and potential alternative explanations for your findings.
• Implications and Applications:  Consider the practical implications of your research. How do your findings contribute to existing knowledge, and how can they be applied in real-world contexts?
• Future Research:  Identify areas for future research and potential improvements in study design. Highlight any limitations or constraints that may have affected your study's outcomes.

By following these steps meticulously, you can conduct a rigorous and informative Quasi-Experimental study that advances knowledge in your field of research.

Quasi-Experimental Design Examples

Quasi-experimental design finds applications in a wide range of research domains, including business-related and market research scenarios. Below, we delve into some detailed examples of how this research methodology is employed in practice:

Example 1: Assessing the Impact of a New Marketing Strategy

Suppose a company wants to evaluate the effectiveness of a new marketing strategy aimed at boosting sales. Conducting a controlled experiment may not be feasible due to the company's existing customer base and the challenge of randomly assigning customers to different marketing approaches. In this scenario, a quasi-experimental design can be employed.

• Independent Variable:  The new marketing strategy.
• Dependent Variable:  Sales revenue.
• Design:  The company could implement the new strategy for one group of customers while maintaining the existing strategy for another group. Both groups are selected based on similar demographics and purchase history , reducing selection bias. Pre-implementation data (sales records) can serve as the baseline, and post-implementation data can be collected to assess the strategy's impact.

Example 2: Evaluating the Effectiveness of Employee Training Programs

In the context of human resources and employee development, organizations often seek to evaluate the impact of training programs. A randomized controlled trial (RCT) with random assignment may not be practical or ethical, as some employees may need specific training more than others. Instead, a quasi-experimental design can be employed.

• Independent Variable:  Employee training programs.
• Dependent Variable:  Employee performance metrics, such as productivity or quality of work.
• Design:  The organization can offer training programs to employees who express interest or demonstrate specific needs, creating a self-selected treatment group. A comparable control group can consist of employees with similar job roles and qualifications who did not receive the training. Pre-training performance metrics can serve as the baseline, and post-training data can be collected to assess the impact of the training programs.

Example 3: Analyzing the Effects of a Tax Policy Change

In economics and public policy, researchers often examine the effects of tax policy changes on economic behavior. Conducting a controlled experiment in such cases is practically impossible. Therefore, a quasi-experimental design is commonly employed.

• Independent Variable:  Tax policy changes (e.g., tax rate adjustments).
• Dependent Variable:  Economic indicators, such as consumer spending or business investments.
• Design:  Researchers can analyze data from different regions or jurisdictions where tax policy changes have been implemented. One region could represent the treatment group (with tax policy changes), while a similar region with no tax policy changes serves as the control group. By comparing economic data before and after the policy change in both groups, researchers can assess the impact of the tax policy changes.

These examples illustrate how quasi-experimental design can be applied in various research contexts, providing valuable insights into the effects of independent variables in real-world scenarios where controlled experiments are not feasible or ethical. By carefully selecting comparison groups and controlling for potential biases, researchers can draw meaningful conclusions and inform decision-making processes.

How to Publish Quasi-Experimental Research?

Publishing your Quasi-Experimental research findings is a crucial step in contributing to the academic community's knowledge. We'll explore the essential aspects of reporting and publishing your Quasi-Experimental research effectively.

Structuring Your Research Paper

When preparing your research paper, it's essential to adhere to a well-structured format to ensure clarity and comprehensibility. Here are key elements to include:

Title and Abstract

• Title:  Craft a concise and informative title that reflects the essence of your study. It should capture the main research question or hypothesis.
• Abstract:  Summarize your research in a structured abstract, including the purpose, methods, results, and conclusions. Ensure it provides a clear overview of your study.

Introduction

• Background and Rationale:  Provide context for your study by discussing the research gap or problem your study addresses. Explain why your research is relevant and essential.
• Research Questions or Hypotheses:  Clearly state your research questions or hypotheses and their significance.

Literature Review

• Review of Related Work:  Discuss relevant literature that supports your research. Highlight studies with similar methodologies or findings and explain how your research fits within this context.
• Participants:  Describe your study's participants, including their characteristics and how you recruited them.
• Quasi-Experimental Design:  Explain your chosen design in detail, including the independent and dependent variables, procedures, and any control measures taken.
• Data Collection:  Detail the data collection methods , instruments used, and any pre-test or post-test measures.
• Data Analysis:  Describe the statistical techniques employed, including any control for confounding variables.
• Presentation of Findings:  Present your results clearly, using tables, graphs, and descriptive statistics where appropriate. Include p-values and effect sizes, if applicable.
• Interpretation of Results:  Discuss the implications of your findings and how they relate to your research questions or hypotheses.
• Interpretation and Implications:  Analyze your results in the context of existing literature and theories. Discuss the practical implications of your findings.
• Limitations:  Address the limitations of your study, including potential biases or threats to internal validity.
• Future Research:  Suggest areas for future research and how your study contributes to the field.

Ethical Considerations in Reporting

Ethical reporting is paramount in Quasi-Experimental research. Ensure that you adhere to ethical standards, including:

• Informed Consent:  Clearly state that informed consent was obtained from all participants, and describe the informed consent process.
• Protection of Participants:  Explain how you protected the rights and well-being of your participants throughout the study.
• Confidentiality:  Detail how you maintained privacy and anonymity, especially when presenting individual data.
• Disclosure of Conflicts of Interest:  Declare any potential conflicts of interest that could influence the interpretation of your findings.

Common Pitfalls to Avoid

When reporting your Quasi-Experimental research, watch out for common pitfalls that can diminish the quality and impact of your work:

• Overgeneralization:  Be cautious not to overgeneralize your findings. Clearly state the limits of your study and the populations to which your results can be applied.
• Misinterpretation of Causality:  Clearly articulate the limitations in inferring causality in Quasi-Experimental research. Avoid making strong causal claims unless supported by solid evidence.
• Ignoring Ethical Concerns:  Ethical considerations are paramount. Failing to report on informed consent, ethical oversight, and participant protection can undermine the credibility of your study.

Guidelines for Transparent Reporting

To enhance the transparency and reproducibility of your Quasi-Experimental research, consider adhering to established reporting guidelines, such as:

• CONSORT Statement:  If your study involves interventions or treatments, follow the CONSORT guidelines for transparent reporting of randomized controlled trials.
• STROBE Statement:  For observational studies, the STROBE statement provides guidance on reporting essential elements.
• PRISMA Statement:  If your research involves systematic reviews or meta-analyses, adhere to the PRISMA guidelines.
• Transparent Reporting of Evaluations with Non-Randomized Designs (TREND):  TREND guidelines offer specific recommendations for transparently reporting non-randomized designs, including Quasi-Experimental research.

By following these reporting guidelines and maintaining the highest ethical standards, you can contribute to the advancement of knowledge in your field and ensure the credibility and impact of your Quasi-Experimental research findings.

Quasi-Experimental Design Challenges

Conducting a Quasi-Experimental study can be fraught with challenges that may impact the validity and reliability of your findings. We'll take a look at some common challenges and provide strategies on how you can address them effectively.

Selection Bias

Challenge:  Selection bias occurs when non-randomized groups differ systematically in ways that affect the study's outcome. This bias can undermine the validity of your research, as it implies that the groups are not equivalent at the outset of the study.

Addressing Selection Bias:

• Matching:  Employ matching techniques to create comparable treatment and control groups. Match participants based on relevant characteristics, such as age, gender, or prior performance, to balance the groups.
• Statistical Controls:  Use statistical controls to account for differences between groups. Include covariates in your analysis to adjust for potential biases.
• Sensitivity Analysis:  Conduct sensitivity analyses to assess how vulnerable your results are to selection bias. Explore different scenarios to understand the impact of potential bias on your conclusions.

History Effects

Challenge:  History effects refer to external events or changes over time that influence the study's results. These external factors can confound your research by introducing variables you did not account for.

Addressing History Effects:

• Collect Historical Data:  Gather extensive historical data to understand trends and patterns that might affect your study. By having a comprehensive historical context, you can better identify and account for historical effects.
• Control Groups:  Include control groups whenever possible. By comparing the treatment group's results to those of a control group, you can account for external influences that affect both groups equally.
• Time Series Analysis :  If applicable, use time series analysis to detect and account for temporal trends. This method helps differentiate between the effects of the independent variable and external events.

Maturation Effects

Challenge:  Maturation effects occur when participants naturally change or develop throughout the study, independent of the intervention. These changes can confound your results, making it challenging to attribute observed effects solely to the independent variable.

Addressing Maturation Effects:

• Randomization:  If possible, use randomization to distribute maturation effects evenly across treatment and control groups. Random assignment minimizes the impact of maturation as a confounding variable.
• Matched Pairs:  If randomization is not feasible, employ matched pairs or statistical controls to ensure that both groups experience similar maturation effects.
• Shorter Time Frames:  Limit the duration of your study to reduce the likelihood of significant maturation effects. Shorter studies are less susceptible to long-term maturation.

Regression to the Mean

Challenge:  Regression to the mean is the tendency for extreme scores on a variable to move closer to the mean upon retesting. This can create the illusion of an intervention's effectiveness when, in reality, it's a natural statistical phenomenon.

Addressing Regression to the Mean:

• Use Control Groups:  Include control groups in your study to provide a baseline for comparison. This helps differentiate genuine intervention effects from regression to the mean.
• Multiple Data Points:  Collect numerous data points to identify patterns and trends. If extreme scores regress to the mean in subsequent measurements, it may be indicative of regression to the mean rather than a true intervention effect.
• Statistical Analysis:  Employ statistical techniques that account for regression to the mean when analyzing your data. Techniques like analysis of covariance (ANCOVA) can help control for baseline differences.

Attrition and Mortality

Challenge:  Attrition refers to the loss of participants over the course of your study, while mortality is the permanent loss of participants. High attrition rates can introduce biases and affect the representativeness of your sample.

Addressing Attrition and Mortality:

• Careful Participant Selection:  Select participants who are likely to remain engaged throughout the study. Consider factors that may lead to attrition, such as participant motivation and commitment.
• Incentives:  Provide incentives or compensation to participants to encourage their continued participation.
• Follow-Up Strategies:  Implement effective follow-up strategies to reduce attrition. Regular communication and reminders can help keep participants engaged.
• Sensitivity Analysis:  Conduct sensitivity analyses to assess the impact of attrition and mortality on your results. Compare the characteristics of participants who dropped out with those who completed the study.

Testing Effects

Challenge:  Testing effects occur when the mere act of testing or assessing participants affects their subsequent performance. This phenomenon can lead to changes in the dependent variable that are unrelated to the independent variable.

Addressing Testing Effects:

• Counterbalance Testing:  If possible, counterbalance the order of tests or assessments between treatment and control groups. This helps distribute the testing effects evenly across groups.
• Control Groups:  Include control groups subjected to the same testing or assessment procedures as the treatment group. By comparing the two groups, you can determine whether testing effects have influenced the results.
• Minimize Testing Frequency:  Limit the frequency of testing or assessments to reduce the likelihood of testing effects. Conducting fewer assessments can mitigate the impact of repeated testing on participants.

By proactively addressing these common challenges, you can enhance the validity and reliability of your Quasi-Experimental study, making your findings more robust and trustworthy.

Conclusion for Quasi-Expermental Design

Quasi-experimental design is a powerful tool that helps researchers investigate cause-and-effect relationships in real-world situations where strict control is not always possible. By understanding the key concepts, types of designs, and how to address challenges, you can conduct robust research and contribute valuable insights to your field. Remember, quasi-experimental design bridges the gap between controlled experiments and purely observational studies, making it an essential approach in various fields, from business and market research to public policy and beyond. So, whether you're a researcher, student, or decision-maker, the knowledge of quasi-experimental design empowers you to make informed choices and drive positive changes in the world.

How to Supercharge Quasi-Experimental Design with Real-Time Insights?

Introducing Appinio , the real-time market research platform that transforms the world of quasi-experimental design. Imagine having the power to conduct your own market research in minutes, obtaining actionable insights that fuel your data-driven decisions. Appinio takes care of the research and tech complexities, freeing you to focus on what truly matters for your business.

Here's why Appinio stands out:

• Lightning-Fast Insights:  From formulating questions to uncovering insights, Appinio delivers results in minutes, ensuring you get the answers you need when you need them.
• No Research Degree Required:  Our intuitive platform is designed for everyone, eliminating the need for a PhD in research. Anyone can dive in and start harnessing the power of real-time consumer insights.
• Global Reach, Local Expertise:  With access to over 90 countries and the ability to define precise target groups based on 1200+ characteristics, you can conduct Quasi-Experimental research on a global scale while maintaining a local touch.

Get free access to the platform!

Get facts and figures 🧠

Want to see more data insights? Our free reports are just the right thing for you!

Wait, there's more

04.11.2024 | 5min read

Trustly uses Appinio’s insights to revolutionize utility bill payments

19.09.2024 | 9min read

Track Your Customer Retention & Brand Metrics for Post-Holiday Success

16.09.2024 | 10min read

Creative Checkup – Optimize Advertising Slogans & Creatives for ROI