what is the importance of critical thinking and problem solving skills in mathematics

Problem solving in mathematics education: tracing its foundations and current research-practice trends

• Original Paper
• Open access
• Published: 30 April 2024
• Volume 56 , pages 211–222, ( 2024 )

Cite this article

You have full access to this open access article

• Manuel Santos-Trigo   ORCID: orcid.org/0000-0002-7144-2098 1  

6420 Accesses

3 Citations

2 Altmetric

Explore all metrics

In tracing recent research trends and directions in mathematical problem-solving, it is argued that advances in mathematics practices occur and take place around two intertwined activities, mathematics problem formulation and ways to approach and solve those problems. In this context, a problematizing principle emerges as central activity to organize mathematics curriculum proposals and ways to structure problem-solving learning environments. Subjects’ use of concrete, abstract, symbolic, or digital tools not only influences the ways to pose and pursue mathematical problems; but also shapes the type of representation, exploration, and reasoning they engage to work and solve problems. Problem-solving foundations that privilege learners’ development of habits of mathematical practices that involve an inquiry method to formulate conjectures, to look for different ways to represent and approach problems, and to support and communicate results shed light on directions of current research trends and the relevance of rethinking curriculum proposals and extending problem-solving environments in terms of teachers/students’ consistent use of digital tools and online developments.

Similar content being viewed by others

Reflections on Problem-Solving

Designing opportunities to learn mathematics theory-building practices

Forging New Opportunities for Problem Solving in Australian Mathematics Classrooms through the First National Mathematics Curriculum

Avoid common mistakes on your manuscript.

1 Introduction and rationale

Mathematical problem solving has been a prominent theme and research area in the mathematics education agenda during the last four decades. Problem-solving perspectives have influenced and shaped mathematics curriculum proposals and ways to support learning environments worldwide (Törner et al., 2007 ; Toh et al., 2023 ). Various disciplinary communities have identified and contributed to connect problem-solving approaches with the students’ learning, construction, and application of mathematical knowledge. The mathematics community recognizes that the formulation and resolution of problems are central activities in the development of the discipline (Halmos, 1980 , Polya, 1945 ). Indeed, the identification and presentation of lists of unsolved mathematical problems have been a tradition that has inspired the mathematics community to approach mathematical problems and to generate mathematical knowledge (Hilbert, 1902 ; Devlin, 2002 ). Thus, mathematical problems, results, and solution attempts provide information regarding what areas and contents were studied at different times during the development of the discipline (Santos-Trigo, 2020a , b ). Cai et al. ( 2023 ) stated that “ …[E]ngaging learners in the activity of problem posing reflects a potentially strong link to the discipline of mathematics” (p. 5). Thurston ( 1994 ) recognized that understanding and applying a mathematical concept implies analysing, coordinating, and integrating diverse meanings (geometric, visual, intuitive, and formal definition) associated with such concept and ways to carry out corresponding procedures and operations in problematic situations.

The centrality of problem-solving in mathematicians’ own work and in their teaching, is incontrovertible. Problem-solving is also a central topic for mathematics educators, who have developed conceptual frameworks to formulate general ideas about problem-solving (as opposed to the specific ideas needed for solving specific problems) (Fried, 2014 ; p.17).

That is, the mathematics education community is interested in analysing and documenting the students’ cognitive and social behaviours to understand and develop mathematical knowledge and problem-solving competencies. “…the idea of understanding how mathematicians treat and solve problems, and then implementing this understanding in instruction design, was pivotal in mathematics education research and practice” (Koichu, 2014 ). In addition, other disciplines such as psychology, cognitive science or artificial intelligence have provided tools and methods to delve into learners’ ways to understand mathematical concepts and to work on problem situations. Thus, members of various communities have often worked in collaboration to identify and relate relevant aspects of mathematical practices with the design and implementation of learning scenarios that foster and enhance students’ mathematical thinking and the development of problem-solving competencies.

2 Methods and procedures

Research focus, themes, and inquiry methods in the mathematical problem-solving agenda have varied and been influenced and shaped by theoretical and methodological developments of mathematics education as a discipline (English & Kirshner, 2016 ; Liljedahl & Cai, 2021 ). Further, research designs and methods used in cognitive, social, and computational fields have influenced the ways in which mathematical problem-solving research are framed. An overarching question to capture shifts and foundations in problem-solving developments was: How has mathematical problem-solving research agenda varied and evolved in terms of ways to frame, pose, and pursue research questions? In addressing this question, it was important to identify and contrast the structure and organization around some published problem-solving reviews (Lester, 1994 ; Törner et al., 2007 ; Rott et al., 2021 ; Liljedahl & Cai, 2021 ; Toh et al., 2023 ) to shed light on a possible route to connect seminal developments in the field with current research trends and perspectives in mathematical problem-solving developments. The goal was to identify common problem-solving principles that have provided a rational and foundations to support recent problem-solving approaches for learners to construct mathematical knowledge and to develop problem-solving competencies. The criteria to select the set of published peer-reviewed studies, to consider in this review, involved choosing articles published in indexed journals (ZDM-Mathematics Education, Educational Studies in Mathematics, Mathematical Thinking and Learning, Journal of Mathematical Behavior, and Journal for Research in Mathematics Education); contributions that appear in International Handbooks in Mathematics Education; and chapters published in recent mathematical problem-solving books. The initial search included 205 publications whose number was reduced to 55, all published in English, based on reviewing their abstracts and conclusions. Around 100 of the initial selection appeared in the references of an ongoing weekly mathematical problem-solving doctoral seminar that has been implemented during the last six years in our department. In addition, some well-known authors in the field were asked to identify their most representative publications to include in the review list. Here, some suggestions were received, but at the end the list of contributions, that appears in the references section, was chosen based on my vision and experience in the field. The goal was to identify main issues or dimensions to frame and analyse recent research trends and perspectives in mathematical problem-solving developments. Thus, seminal reviews in the field (Schoenfeld, 1992 ; Lester, 1994 ; Törner et al., 2007 ) provided directions on ways to structure and select the questions used to analyse the selected contributions. Table  1 shows chosen issues that resemble features of an adjusted framework that Lester ( 1994 ) proposed to organize, summarize, and analyse problem-solving developments in terms of research emphasis (themes and research questions), methodologies (research designs and methods), and achieved results that the problem-solving community addressed during the 1970–1994 period. Furthermore, relevant shifts in the mathematical problem-solving agenda could be identified and explained in terms of what the global mathematics education and other disciplines pursue at different periods.

It is important to mention that the content and structure of this paper involve a narrative synthesis of selected articles that includes contributions related to mathematical problem-solving foundations and those that address recent developments published in the last 9 years that involve the use of digital technologies. Table  1 shows themes, issues, and overarching questions that were used to delve into problem-solving developments.

To contextualize the current state of art in the field, it is important to revisit problem-solving principles and tenets that provide foundations and a rationale to centre and support the design and implementation of learning environments around problem-solving activities (Santos-Trigo, 2020a , b ). The identification of mathematical problem-solving foundations also implies acknowledging what terms, concepts, and language or discourse that the problem-solving community has used to refer to and frame problem-solving approaches. For example, routine and nonroutine tasks, heuristic and metacognitive strategies, students’ beliefs, mathematical thinking and practices, resources, orientations, etc. are common terms used to explain, foster, and characterize students’ problem-solving behaviours and performances. Recently, the consistent use of digital technologies in educational tasks has extended the problem-solving language to include terms such as subjects’ tool appropriation, dynamic models, dragging or moving orderly objects, tracing loci, visual or empirical solution, ChatGPT prompts, etc.

3 On mathematical problem-solving foundations and the problematizing principle

There might be different ways to interpret and implement a problem-solving approach for students to understand concepts and to solve problems (Törner, Schoenfeld, & Reiss, 2007 ; Toh et al., 2023 ); nevertheless, there are common principles or tenets that distinguish and support a problem-solving teaching/learning environment. A salient feature in any problem-solving approach to learn mathematics is a conceptualization of the discipline that privileges and enhance the students’ development of mathematical practices or reasoning habits of mathematical thinking (Cuoco, et, al., 1996 ; Dick & Hollebrands, 2011 ; Schoenfeld, 2022 ). In this context, students need to conceptualize and think of their own learning as a set of dilemmas that are represented, explored, and solved in terms of mathematical resources and strategies (Santos-Trigo, 2023 ; Hiebert et al., 1996 ).

Furthermore, students’ problem-solving experiences and behaviours reflect and become a way of thinking that is consistent with mathematics practices and is manifested in terms of the activities they engage throughout all problem-solving phases. Thus, they privilege the development of mathematics habits such as to always look for different ways to model and explore mathematical problems, to formulate conjectures, and to search for arguments to support them, share problem solutions, defend their ideas, and to develop a proper language to communicate results. In terms of connecting ways of developing mathematical knowledge and the design of learning environments to develop mathematical thinking and problem-solving competencies, Polya ( 1945 ) identifies an inquiry approach for students to understand, make sense, and apply mathematical concepts. He illustrated the importance for students to pose and pursue different questions around four intertwined problem-solving phases: Understanding and making sense of the problem statement (what is the problem about? What data are provided? What is asked to find? etc.), the design of a solution plan (how the problem can be approached? ), the implementation of such plan (how the plan can be achieved? ), and the looking-back phase that involves reviewing the solution process (data used, checking the involved operations, consistency of units, and partial and global solution), generalizing the solution methods and posing new problems. Indeed, the looking-back phase involves the formulation of new or related problems (Toh et al., 2023 ). “For Pólya, mathematics was about inquiry; it was about sense making; it was about understanding how and why mathematical ideas fit together the ways they do” (cited in Schoenfeld, 2020 , p. 1167).

Likewise, the Nobel laureate I. I. Rabi mentioned that, when he came home from school, “while other mothers asked their kids ‘ Did you learn anything today ?’ [my mother] would say, ‘ Izzy, did you ask a good question today ?’” (Berger, 2014 , p.67).

Thus, the problematizing principle is key for students to engage in mathematical problem-solving activities, and it gets activated by an inquiry or inquisitive method that is expressed in terms of questions that students pose and pursue to delve into concepts meaning, representations, explorations, operations, and to work on mathematical tasks (Santos-Trigo, 2020a , b ).

4 The importance of mathematical tasks and the role of tools in problem-solving perspectives

In a problem-solving approach, learners develop a way of thinking to work on different types of tasks that involve a variety of context and aims (Cai & Hwang, 2023 ). A task might require students to formulate a problem from given information, to estimate how much water a family spend in one year, to prove a geometry theorem, to model genetic sequences or to understand the interplay between climate and geography. In this process, students identify mathematical resources, concepts, and strategies to model and explore partial and global solutions, and ways to extend solution methods and results. Furthermore, mathematical tasks or problems are essential for students to engage in mathematical practice and to develop problem-solving competencies. Task statements should be situated in different contexts including realistic, authentic, or mathematical domains, and prompts or questions to solve or respond or even provide information or data for students to formulate and solve their own problems (problem posing). Current events or problematic situations such as climate change, immigration, or pandemics not only are part of individuals concerns; but also, a challenge for teachers and students to model and analyze those complex problems through mathematics and others disciplines knowledge (English, 2023 ). Santos-Trigo ( 2019 ) proposed a framework to transform exercises or routine textbook problems into a series of nonroutine tasks in which students have an opportunity to dynamically model, explore, and extend, the initial problem. Here, the use of technology becomes important to explore the behavior of some elements within the model to find objects’ mathematical relationships. That is, students work on tasks in such a way that even routine problems become a starting point for them to engage in mathematical reflection to extend the initial nature of the task (Santos-Trigo & Reyes-Martínez, 2019 ). Recently, the emergence of tools such as the ChatGPT has confirmed the importance for learners to problematize situations, including complex problems, in terms of providing prompts or inputs that the tool processes and answers. Here, students analyze the tool’ responses and assess its pertinence to work and solve the task. Indeed, a way to use ChatGPT involves that students understand or make sense of the problem statement and pose questions (inputs or prompts) to ask the tool for concept information or ways to approach or solve the task. Then, students analyze the relevance, viability, and consistency of the tool’s answer and introduce new inputs to continue with the solution process or to look for another way to approach the task. Based on the ChatGPT output or task solution, students could always ask whether the tool can provide other ways to solve the task.

5 Main problem-solving research themes and results

In this section the focus will be on identifying certain problem-solving developments that have permeated recent directions of the field. One relates to the importance of extending research designs to analyse and characterize learners’ problem-solving process to work on different types of tasks. Another development involves ways in which theoretical advances in mathematics education have shaped the mathematical problem-solving research agenda and the extent to which regional or national educational systems or traditions influence the developments of conceptual frameworks in the field and ways to implement problem-solving activities within the corresponding system. Finally, research results in the field have provided directions to design and implement curriculum proposals around the world and these proposals have evolved in terms of both content structure and classroom dynamics including the use of digital technologies. Santos-Trigo ( 2023 ) stated that the teachers and students’ systematic use of digital technologies not only expands their ways of reasoning and solving mathematical problems; but also opens new research areas that aim to analyse the integration of several digital tools in curriculum proposals and learning scenarios. The focus of this review will be on presenting problem-solving directions and results in the last 9 years; however, it became relevant to identify and review what principles and tenets provided bases or foundations to support and define current research trends and directions in the field. That is, accumulated research that has contributed to advance and expand the problem-solving research agenda included shifts in the tools used to delve into learners’ problem approaches, the development of conceptual frameworks to explain and characterize students’ mathematical thinking, the tools used to work on mathematical tasks (from paper and pencil, ruler and compass or semiotic tools to digital apps), and in the design of curriculum proposals and the implementation of problem-solving learning scenarios.

5.1 Relevant shifts in problem-solving developments and results

Questions used to analyse important developments in the field include: What research designs and tools are used to foster and analyse learners’ problem-solving performances? How have conceptual frameworks evolved to pose and frame research questions in the field? How have accumulated research results in the field been used to support curriculum proposals and their implementation?

5.1.1 Methodological and research paradigms

Research designs in problem-solving studies have gradually moved from quantitative or statistical paradigms to qualitative perspectives that involve data collection from different sources such as task-based interviews, fieldnotes from observations, students’ written reports, etc. to analyse students’ problem-solving approaches and performances. Trustworthiness of results included triangulating and interpreting data sources from students’ videotapes transcriptions, outside observer notes, class observations, etc. (Stake, 2000 ). Hence, the work of Krutestkii ( 1976 ) was seminal in providing tools to delve into the students’ thinking while solving mathematical tasks. His research program aimed to study the nature and structure of children’ mathematical abilities. His methodological approach involved the use of student’s task-based interviews, teachers, and mathematicians’ questionaries to explore the nature of mathematical abilities, the analysis of eminent mathematicians and physicists regarding their nature and emergence of their talents and case studies of gifted children in mathematics. A major contribution of his research was the variety of mathematical tasks used to explore and analyse the mathematical abilities of school children. Recently, the mathematical problem-posing agenda has been revisited to advance conceptual frameworks to enhance the students’ formulation of problems to learn concepts and to develop problem-solving competencies (Cai et al., 2023 ). In general, the initial qualitative research tendency privileged case studies where individual students were asked to work on mathematical tasks to document their problem-solving performances. Later, research designs include the students’ participation in small groups and the analysis of students’ collaboration with the entire group (Brady et al., 2023 ). Bricolage frameworks that share tenets and information from different fields have become a powerful tool for researchers to understand complex people’ problem-solving proficiency (Lester, 2005 ; English, 2023 ).

5.1.2 Theoretical developments in mathematics education

In mathematics education, the constructivism perspective became relevant to orient and support research programs. Specifically, the recognition that students construct mathematical concepts and ideas through active participation as a part of a learning community that fosters and values what they bring into the classroom (eliciting students’ understanding) and sharing and discussing with peers their ways to work on mathematical activities. Further, it was recognized that students’ learning of mathematics takes place within a sociocultural environment (situated learning) that promotes the students’ interaction in small groups, pairs, and whole group discussions. Thus, problem-solving environments transited from teachers being a main figure to organize learning activities and to model problem-solving behaviours to being centred on students’ active participation to work on a variety of mathematical tasks as a part of a learning community (Lester & Cai, 2016 ). English ( 2023 ) proposed A STEM-based problem-solving framework that addresses the importance of a multidisciplinary approach and experiences to work on complex problems. Here, students develop a system of inquiry that integrates critical thinking, mathematical modelling, and a creative and innovative approach to deal with problematic situations situated in contexts beyond school problems. The STEM-based problem-solving framework enhances and favours the students’ development of multidisciplinary thinking to formulate and approach challenging problematic situations. To this end, they need to problematize information to characterize local and global problems and to collaboratively work on feasible approaches and solutions. It integrates 21st century skills that include an inquiry problem-solving approach to develop and exhibit critical thinking, creativity, and innovative solutions.

5.1.3 Countries or regional education traditions and their influence on the problem-solving agenda

The emergence of problem-solving frameworks takes place within an educational and socio-cultural context that provides conditions for their development and dissemination, but also limitations in their applications inside the mathematics education community. Brady et al. ( 2023 ) pointed out that:

…shifts in the theoretical frameworks of mathematics education researchers favored a widening of the view on problem solving from information-processing theories toward sociocultural theories that encouraged a conception of problem-solving as situated cognition unfolding within a community of practice (p. 34).

In addition, regional or national educational systems and research traditions also shape the problem-solving research and practice agenda. For example, in France, problem-solving approaches and research are framed in terms of two relevant theoretical and practical frameworks: Theory of Didactic Situation and the Anthropological Theory of Didactics (Artigue & Houdement, 2007 ). While, in the Netherlands, problem-solving approaches are situated within the theory of Realistic Mathematics that encourages and supports the students’ construction of meaning of concepts and methods in terms of modelling real-life and mathematical situations (Doorman et al., 2007 ). Ding et al. ( 2022 ) stated that the Chinese educational system refers to problem solving as an instructional goal and an approach to learn mathematics. Here, students deal with different types of problem-solving activities that include finding multiple solutions to one problem, one solution to multiple problems, and one problem multiple changes. Thus, ‘teaching with variation’ is emphasized in Chinese instruction in terms of “variations in solutions, presentations, and conditions/conclusions” (p. 482). Cai and Rott ( 2023 ) proposed a general problem-posing process model that distinguishes four problem-posing phases: Orientation (understanding the situation and what is required or is asked to pose); Connection that involves finding out or generating ideas and strategies to pose problems in different ways such as varying the given situation, or posing new problems; Generation refers to making the posed problem visible for others to understand it; and Reflection involves reflecting on her/his own process to pose the problem including ways to improve problem statements. The challenge in this model is to make explicit how the use of digital technologies can contribute to providing conditions for students to engage in all phases around problem- posing process.

5.1.4 Curriculum proposals and problem-solving teaching/learning scenarios

In the USA, the Common Core State Mathematics Standards curriculum proposal (CCSMS) identifies problem solving as a process standard that supports core mathematical practices that involve reasoning and proof, communication, representation, and connections. Thus, making sense of problems and persevering in solving them, reasoning abstractly and quantitatively, constructing viable arguments and critiquing the reasoning of others, modelling with mathematics, etc. are essential activities for students to develop mathematics proficiency and problem-solving approaches (Schoenfeld, 2023 ). In Singapore, the curriculum proposal identifies problem solving as the centre of its curriculum framework that relates its development with the study of concepts, skills, processes, attitudes, and metacognition (Lee et al., 2019 ). Recently, educational systems have begun to reform curriculum proposals to relate what the use of digital technologies demands in terms of selecting and structuring mathematical contents and ways to extend instructional settings (Engelbrecht & Borba, 2023 ). Indeed, Engelbrecht et al. ( 2023 ) identify what they call a classroom in movement or a distributed classroom - that transforms traditional cubic spaces to study the discipline into a movable setting that might combine remote and face-to-face students work.

It is argued that previous results in mathematical problem-solving research not only have contributed to recognize what is relevant and what common tenets distinguish and support problem-solving approaches; but also have provided bases to identify and pursue current problem-solving developments and directions. Hence, the consistent and coordinated use of several digital technologies and online developments (teaching and learning platforms) has opened new routes for learners to represent, explore, and work on mathematical problems; and to engage them in mathematical discussions beyond formal class settings. How does the students’ use of digital technologies expand the ways they reason and solve mathematical problems? What changes in classroom environments and physical settings are needed to recognize and include students’ face-to-face and remote work? (Engelbrecht et al., 2023 ).

In the next sections, the goal is to characterize the extent to which the consistent use of digital technologies and online developments provides affordances to restructure mathematical curriculum proposals and classrooms or learning settings and to enhance and expand students’ mathematical reasoning.

6 Current mathematical problem-solving trends and developments: the use of digital technologies

Although the use of technologies has been a recurrent theme in research studies, curriculum proposals, and teaching practices in mathematics education; during the COVID-pandemic lockdown, all teachers and students relied on digital technologies to work on mathematical tasks. At different phases, they developed and implemented not only novel paths to present, discuss, and approach teaching/learning activities; but also, ways to monitor and assess students’ problem-solving performances. When schools returned to teachers and students’ face-to-face activities, some questions emerged: What adjustments or changes in school practices are needed to consider and integrate those learning experiences that students developed during the social confinement? What digital tools should teachers and students use to work on mathematical tasks? How should teaching/learning practices reconcile students remote and face-to-face work? To address these questions, recent studies that involve ways to integrate technology in educational practices were reviewed, and their main themes and findings are organized and problematized to shed light on what the use of digital technologies contributes to frame and support learning environments.

6.1 The use of technology to reconceptualize students mathematical learning

There are different studies that document the importance and ways in which the students’ use of tools such as CAS or Excel offers an opportunity for them to think of concepts and problems in terms of different representations to transit from intuitive, visual, or graphic to formal or analytical reasoning (Arcavi et al., 2017 ). Others digital technologies, such as a Dynamic Geometry System Footnote 1 DGS, provide affordances for students to dynamically represent and explore mathematical problems. In students’ use of digital technologies, the problematizing principle becomes relevant to transform the tool into an instrument to work on mathematical tasks. Santos-Trigo ( 2019 ) provides examples where students rely on GeoGebra affordances to reconstruct figures that are given in problem statements; to transform routine problem into an investigation task; to model and explore tasks that involve variational reasoning; and to construct dynamic configurations to formulate and support mathematical relations. In this process, students not only exhibit diverse problem-solving strategies; but also, identify and integrate and use different concepts and resources that are studied in algebra, geometry, and calculus. That is, the use of technology provides an opportunity for students to integrate and connect knowledge from diverse areas or domains. For instance, Sinclair and Ferrara ( 2023 ) used the multi-touch application (TouchCounts) for children to work on mathematical challenging tasks.

6.2 The use of digital technologies to design a didactic route

There is indication, that the use of digital technologies offers different paths for students to learn mathematics (Leung & Bolite-Frant, 2015 ; Leung & Baccaglini-Frank, 2017 ). For instance, in the construction of a dynamic model of a problem, they are required to think of concepts and information embedded in the problem in terms of geometric representation or meaning. Thus, focusing on ways for students to represent and explore concepts geometrically could be the departure point to understand concepts and to solve mathematical problems. In addition, students can explore problems’ dynamic models (dragging schemes) in terms of visual, empirical, and graphic representations to initially identify relations that become relevant to approach and solve the problems. Thus, tool affordances become relevant for students to detect patterns, to formulate conjectures and to transit from empirical to formal argumentation to support problem solutions (Pittalis & Drijvers, 2023 ). Engelbrecht and Borba ( 2023 ) recognized that the prominent use of digital technologies in school mathematics has produced pedagogical shifts in teaching and learning practices to “encourage more active students learning, foster greater engagement, and provide more flexible access to learning’ (p. 1). Multiple use technologies such as internet, communication apps (ZOOM, Teams, Google Meet, etc.) become essential tools for teachers and students to present, communicate, and share information or to collaborate with peers. While tools used to represent, explore, and delve into concepts and to work and solve mathematical problems (Dynamic Geometry Systems, Wolframalpha, etc.) expand the students’ ways of reasoning and solving problems. Both types of technologies are not only important for teachers and students to continue working on school tasks beyond formal settings, but they also provide students with an opportunity to consult online resources such as Wikipedia or KhanAcademy to review or extend their concepts understanding, to analyse solved problems, and to contrast their teachers’ explanation of themes or concepts with those provided in learning platforms.

6.3 Students’ access to mathematics learning

Nowadays, cell phones are essential tools for people or students to interact or to approach diverse tasks and an educational challenge is how teachers/students can use them to work on mathematical tasks. During the COVID-19 social confinement, students relied on communication apps not only to interact with their teachers during class lectures; but also, to keep discussing tasks with peers beyond formal class meetings. That is, students realized that with the use of technology they could expand their learning space to include sharing and discussing ideas and problem solutions with peers beyond class sessions, consulting online learning platforms or material to review or extend their concepts understanding, and to watch videos to contrast experts’ concepts explanations and those provided by their teachers. In this perspective, the use of digital technologies increases the students’ access to different resources and the ways to work on mathematical tasks. Thus, available digital developments seem to extend the students collaborative work in addition to class activities. Furthermore, the flipped classroom model seems to offer certain advantages for students to learn the discipline and this model needs to be analysed in terms of what curriculum changes and ways to assess or monitor students learning are needed in its design and implementation (Cevikbas & Kaiser, 2022 ).

6.4 Changes in curriculum and mathematical assessment

It is recognized that the continuous development and availability of digital technologies is not only altering the ways in which individuals interact and face daily activities; but is also transforming educational practices and settings. Likewise, people’s concerns about multiple events or global problems such climate change, immigration, educational access, renewable resources, or racial conflicts or wars are themes that permeate the educational arena. Thus, curriculum reforms should address ways to connect students’ education with the analysis of these complex problems. English ( 2023 ) stated that:

The ill-defined problems of today, coupled with unexpected disruptions across all walks of life, demand advanced problem-solving by all citizens. The need to update outmoded forms of problem solving, which fail to take into account increasing global challenges, has never been greater (p.5).

In this perspective, mathematics curriculum needs to be structured around essential contents and habits of mathematical thinking for students to understand and make sense of real-world events that lead them to formulate, represent, and deal with a variety of problem situations. “Educators now increasingly seek to emphasise the practical applications of mathematics, such as modelling real-life scenarios and understanding statistical data (Engelbrecht & Borba, 2023 , p. 7). For instance, during the pandemic it was important to problematize the available data to follow, analyze and predict its spread behavior and to propose health measures to reduce people contagion. Thus, exponential functions, graphics, and their interpretations, data analysis, etc. were important mathematics content to understand the pandemic phenomena. Drijvers and Sinclair ( 2023 ) recognized that features of computational thinking share common grounds with mathematical thinking in terms of problem-solving activities that privilege model construction, the use of algorithms, abstraction processes and generalization of results. Thus, “a further integration of computational thinking in the mathematics curriculum is desirable”. In terms of ways to assess and monitor students’ learning, the idea is that with the use of a digital tool (digital wall or log), students could organize, structure, register, and monitor their individual and group work and learning experiences. That is, they could periodically report and share what difficulties they face to understand concepts or to work on a task, what questions they posed, what sources consult, etc. The information that appears in the digital wall is shared within the group and the teacher and students can provide feedback or propose new ideas or solutions (Santos-Trigo et al., 2022 ).

6.5 The integration of technologies and the emergence of conceptual frameworks

Institutions worldwide, in general, are integrating the use of different technologies in their educational practices, and they face the challenge to reconcile previous pandemic models and post confinement learning scenarios. “A pedagogical reason for using technology is to empower learners with extended or amplified abilities to acquire knowledge…technology can empower their cognitive abilities to reason in novice ways (Leung, 2011 , p. 327). Drijvers and Sinclair ( 2023 ) proposed a five-dimensional framework to delve into the rationale and purposes for the mathematics education community to integrate the use of digital technologies in mathematical teaching environments and students learning. The five interrelated categories address issues regarding how teachers and students’ use of digital technology contributes to reconceptualize and improve mathematics learning; to understand and explain how students’ mathematics learning develops; to design environments for mathematics learning; to foster and provide equitable access to mathematics learning; and to change mathematics curricula and teaching and assessment practices (Drijvers & Sinclair, 2023 ). Schoenfeld ( 2022 ) stated that “The challenge is to create robust learning environments that support every student in developing not only the knowledge and practices that underlie effective mathematical thinking, but that help them develop the sense of agency to engage in sense making” (p. 764). Højsted et al. ( 2022 ) argue about the importance of adjusting theoretical frameworks to explicitly integrate the use of digital technologies such as DGS and Computer Algebra Systems (CAS) in teaching practices. They referred to the Danish “Competencies and Mathematical Learning framework” (KOM) that gets articulated through tenets associated with the Theory of Instrumental Orchestration (TIO) and the notion of Justification Mediation (JM). In general terms, the idea is that learners get explicitly involved in a tool’ appropriation process that transforms the artifact into an instrument to understand concepts and to solve mathematical problems. That is, learners’ tool appropriation involves the development of cognitive schemata to rely on technology affordances to work on mathematical tasks. Koichu et al. ( 2022 ) pointed out that the incorporation of problem-solving approaches in instruction should be seen as a specific case of implementing innovation. To this end, they proposed a framework of problem-solving implementation chain that involves “a sequence of actions and interactions beginning with the development of a PS resource by researchers, which teachers then engage with in professional development (PD), and finally, teachers and students make use of in classrooms” (p. 4). In this case, problem-solving resources include the design of problematic situations (tasks) to engage students in mathematical discussions to make sense of problem statements or to ask them to pose a task.

7 Reflections and concluding remarks

Throughout different periods, the research and practice mathematical problem-solving agenda has contributed significantly to understand not only essentials in mathematical practices; but also, the development of conceptual frameworks to explain and document subjects’ cognitive, social, and affective behaviours to understand mathematical concepts and to develop problem-solving competencies. Leikin and Guberman ( 2023 ) pointed out that “…problem-solving is an effective didactical tool that allows pupils to mobilize their existing knowledge, construct new mathematical connections between known concepts and properties, and construct new knowledge in the process of overcoming challenges embedded in the problems” (p. 325). The study of people cognitive functioning to develop multidisciplinary knowledge and to solve problems involves documenting ways in which individuals make decisions regarding ways to organize their subject or disciplinary learning (how to interact with teachers or experts and peers; what material to consult, what tools to use, how to monitor their own learning, etc.) and to engage in disciplinary practices to achieve their learning goals. Both strategic and tactic decisions shape teachers and students’ ways to work on mathematical tasks. Kahneman ( 2011 ) shed light on how human beings make decisions to deal with questions and problematic situations. He argues that individuals rely on two systems to make decisions and engage in thinking processes; system one (fast thinking) that involves automatic, emotional, instinctive reasoning and system two (slow thinking) that includes logical, deliberative, effortful, or conscious reasoning. In educational tasks, the idea is that teachers and students develop experiences based on the construction and activation of system two. Thus, how teachers/students decide what tools or digital developments to use to work on mathematical problems becomes a relevant issue to address in the mathematics education agenda. Recent and consistent developments and the availability of digital technologies open novel paths for teachers and students to represent, explore, and approach mathematical tasks and, provide different tools to extend students and teachers’ mathematical discussions beyond classroom settings. In this perspective, it becomes important to discuss what changes the systematic use of digital technologies bring to the mathematics contents and to the ways to frame mathematical instruction. For example, the use of a Dynamic Geometry System to model and explore calculus, geometry or algebra classic problems dynamically not only offer students an opportunity to connect foundational concepts such as rate of change or the perpendicular bisector concept to geometrically study variational phenomena or conic sections; but also, to engage them in problem-posing activities (Santos-Trigo et al., 2021 ). Thus, teachers need to experience themselves different ways to use digital technologies to work on mathematical tasks and to identify instructional paths for students to internalize the use of digital apps as an instrument to understand concepts and to pose and formulate mathematical problems. Specifically, curriculum proposal should be structured around the development of foundational concepts and problem-solving strategies to formulate and pursue complex problems such as those involving climate changes, wealth distribution, immigration, pollution, mobility, connectivity, etc. To formulate and approach these problems, students need to develop a multidisciplinary thinking and rely on different tools to represent, explore, and share and continuously report partial solutions. To this end, they are encouraged to work with peers and groups as a part of learning community that fosters and values collective problem solutions. Finding multiple paths to solve problems becomes important for students to develop creative and innovative problem solutions (Leikin & Guberman, 2023 ). In this perspective, learning environments should provide conditions for students to transform digital applications in problem-solving tools to work on problematic situations. Online students’ assignments become an important component to structure and organize students and teachers’ face-to-face interactions. Likewise, the use of technology can also provide a tool for students to register and monitor their work and learning experiences. A digital wall or a problem-solving digital notebook (Santos-Trigo et al., 2022 ) could be introduced for students to register and monitor their learning experiences. Here, Students are asked to record on a weekly basis their work, questions, comments, and ideas that include: Questions they pose to understand concepts and problem statements; online resources and platforms they consult to contextualize problems and review and extend their understanding of involved concepts; concepts and strategies used to solve problems through different approaches; the Identification of other problems that can be solved with the methods that were used to solve the problem; digital technologies and online resources used to work on and solve the problem; dynamic models used to solve the problem and strategies used to identify and explore mathematical relations (dragging objects, measuring object attributes, tracing loci, using sliders, etc.; the formulation of new related problems including possible extensions for the initial problem; discussion of solutions of some new problems; and short recorded video presentation of their work and problem solutions. That is, the digital wall becomes an space for learners to share their work and to contrast and reflect on their peers work including extending their problem-solving approaches based on their teachers feedback and peers’ ideas or solutions.

The term Dynamic Geometry System is used, instead of Dynamic Geometry Environment or Dynamic Geometry Software, to emphasize that the app or tool interface encompasses a system of affordances that combines the construction of dynamic models, the use of Computer Algebra Systems and the use spreadsheet programs.

Arcavi, A., Drijvers, P., & Stacy, K. (2017). The learning and teaching of algebra. Ideas, insights, and activities . NY: Routledge. ISBN 9780415743723.

Artigue, M., & Houdement, C. (2007). Problem solving in France: Didactic and curricular perspectives. ZDM Int J Math Educ , 39 (5–6), 365–382. https://doi.org/10.1007/s11858-007-0048-x .

Article   Google Scholar  

Berger, W. (2014). A more beautiful question . Bloomsbury Publishing. Kindle Edition.

Brady, C., Ramírez, P., & Lesh, R. (2023). Problem posing and modeling: Confronting the dilemma of rigor or relevance. In T. L. Toh et al. (Eds.), Problem Posing and Problem Solving in Mathematics Education, pp: 33–50, Singapore: Springer. https://doi.org/10.1007/978-981-99-7205-0_3 .

Cai, J., & Hwang, S. (2023). Making mathematics challenging through problem posing in classroom. In R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, Springer: Switzerland, pp. 115–145, https://doi.org/10.1007/978-3-031-18868-8_7 .

Cai, J., & Rott, B. (2023). On understanding mathematical problem-posing processes. ZDM – Mathematics Education , 56 , 61–71. https://doi.org/10.1007/s11858-023-01536-w .

Cai, J., Hwang, S., & Melville, M. (2023). Mathematical problem-posing research: Thirty years of advances building on the publication of on mathematical problem solving. In J. Cai et al. (Eds.), Research Studies on Learning and Teaching of Mathematics, Research in Mathematics Education, Springer: Switzerland, pp: 1–25. https://doi.org/10.1007/978-3-031-35459-5_1 .

Cevikbas, M., & Kaiser, G. (2022). Can flipped classroom pedagogy offer promising perspectives for mathematics education on pan- demic-related issues? A systematic literature review. ZDM – Math- ematics Education . https://doi.org/10.1007/s11858-022-01388-w .

Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior , 15 , 375–402.

Devlin, K. (2002). The millennium problems. The seven greatest unsolved mathematical puzzles of our time . Granta.

Dick, T. P., & Hollebrands, K. F. (2011). Focus in high school mathematics: Technology to support reasoning and sense making . National Council of Teachers of Mathematics, NCTM: Reston Va. ISBN 978-0-87353-641-7.

Ding, M., Wu, Y., Liu, Q., & Cai, J. (2022). Mathematics learning in Chinese contexts. ZDM -Mathematics Education , 54 , 577–496. https://doi.org/10.1007/s11858-022-01385-z .

Doorman, M., Drijvers, P., Dekker, T., Van den Heuvel- Panhuizen, M., de Lange, J., & Wijers, M. (2007). Problem solving as a challenge for mathematics education in the Netherlands. ZDM Int J Math Educ , 39 (5–6), 405–418. https://doi.org/10.1007/s11858-007-0043-2 .

Drijvers, P., & Sinclair, N. (2023). The role of digital technologies in mathematics education: Purposes and perspectives. ZDM-Mathematics Education . https://doi.org/10.1007/s11858-023-01535-x .

Engelbrecht, J., & Borba, M. C. (2023). Recent developments in using digital technology in mathematics education. ZDM -Mathematics Education . https://doi.org/10.1007/s11858-023-01530-2 .

Engelbrecht, J., Borba, M. C., & Kaiser, G. (2023). Will we ever teach mathematics again in the way we used to before the pandemic? ZDM– Mathematics Education , 55 , 1–16. https://doi.org/10.1007/s11858-022-01460-5 .

English, L. D. (2023). Ways of thinking in STEM-based problem solving. ZDM -Mathematics Education . https://doi.org/10.1007/s11858-023-01474-7 .

English, L. D., & Kirshner, D. (Eds.). (2016). Handbook of international research in mathematics education . NY. ISBN: 978-0-203-44894-6 (ebk). https://www.routledge.com/Handbook-of-International-Research-in-Mathematics-Education/English-Kirshner/p/book/9780415832045

Fried, M. N. (2014). Mathematics & mathematics education: Searching for common ground. In M.N. Fried, T. Dreyfus (Eds.), Mathematics & Mathematics Education: Searching for 3 Common Ground , Advances in Mathematics Education, pp: 3–22. https://doi.org/10.1007/978-94-007-7473-5_1 . NY: Springer.

Halmos, P. (1980). The heart of mathematics. American Mathematical Monthly , 87 (7), 519–524.

Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K., Human, P., Murray, H., et al. (1996). Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher , 25 (4), 12–21.

Hilbert, D. (1902). Mathematical problems. Bulletin of the American Mathematical Society , 8 , 437–479.

Højsted, I. H., Geranius, E., & Jankvist, U. T. (2022). Teachers’ facilitation of students’ mathematical reasoning in a dynamic geometry environment: An analysis through three lenses. In U. T. Jankvist, & E. Geraniou (Eds.), Mathematical competencies in the Digital era (pp. 271–292). Springer. https://doi.org/10.1007/978-3-031-10141-0_15 .

Kahneman, D. (2011). Thinking, fast and slow . Farrar, Straus and Giroux.

Koichu, B. (2014). Problem solving in mathematics and in mathematics education. In M.N. Fried, T. Dreyfus (Eds.), Mathematics & Mathematics Education: Searching for 113 Common Ground , Advances in Mathematics Education, pp: 113–135. Dordrecht: Springer. https://doi.org/10.1007/978-94-007-7473-5_8 .

Koichu, B., Cooper, J., & Widder, M. (2022). Implementation of problem solving in school: From intended to experienced. Implementation and Replication Studies in Mathematics Education , 2 (1), 76–106. https://doi.org/10.1163/26670127-bja10004 .

Krutestkii, V. A. (1976). The psychology of mathematical abilities in school children . University of Chicago Press, Chicago. ISBN: 0-226-45492-4.

Lee, N. H., Ng, W. L., & Lim, L. G. P. (2019). The intended school mathematics curriculum. In T. L. Toh et al. (Eds.), Mathematics Education in Singapore , Mathematics Education – An Asian Perspective, pp: 35–53. https://doi.org/10.1007/978-981-13-3573-0_3 .

Leikin, R., & Guberman, R. (2023). Creativity and challenge: Task complexity as a function of insight and multiplicity of solutions. R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, pp: 325–342. https://doi.org/10.1007/978-3-031-18868-8_17 .

Lester, F. K. Jr. (1994). Musing about mathematical problem-solving research: 1970–1994. Journal for Research in Mathematics Education , 25 (6), 660–675.

Lester, F. K. Jr. (2005). On the theoretical, conceptual, and philosophical foundation for research in mathematics education. Zdm Mathematics Education , 37 (6), 457–467. https://doi.org/10.1007/BF02655854 .

Lester, F. K. Jr., & Cai, J. (2016). Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In P. Felmer, et al. (Eds.), Posing and solving Mathematical problems, Research in Mathematics Education (pp. 117–135). Springer. https://doi.org/10.1007/978-3-319-28023-3_8 .

Leung, A. (2011). An epistemic model of task design in dynamic geometry environment. Zdm , 43 , 325–336. https://doi.org/10.1007/s11858-011-0329-2 .

Leung, A., & Baccaglini-Frank, A. (Eds.). (2017). (Eds.). Digital Technologies in Designing Mathematics Education Tasks, Mathematics Education in the Digital Era 8, https://doi.org/10.1007/978-3-319-43423-0_1 .

Leung, A., & Bolite-Frant, J. (2015). Designing mathematics tasks: The role of tools. In A. Watson, & M. Ohtani (Eds.), Task design in mathematics education (pp. 191–225). New ICMI Study Series. https://doi.org/10.1007/978-3-319-09629-2_6 .

Liljedahl, P., & Cai, J. (2021). Empirical research on problem solving and problem pos- ing: A look at the state of the art. ZDM — Mathematics Education , 53 (4), 723–735. https://doi.org/10.1007/s11858-021-01291-w .

Pittalis, M., & Drijvers, P. (2023). Embodied instrumentation in a dynamic geometry environment: Eleven-year‐old students’ dragging schemes. Educational Studies in Mathematics , 113 , 181–205. https://doi.org/10.1007/s10649-023-10222-3 .

Pólya, G. (1945).; 2nd edition, 1957). How to solve it . Princeton University Press.

Rott, B., Specht, B., & Knipping, C. (2021). A descritive phase model of problem-solving processes. ZDM -Mathematics Education , 53 , 737–752. https://doi.org/10.1007/s11858-021-01244-3 .

Santos-Trigo, M. (2019). Mathematical Problem Solving and the use of digital technologies. In P. Liljedahl and M. Santos-Trigo (Eds.). Mathematical Problem Solving. ICME 13 Monographs , ISBN 978-3-030-10471-9, ISBN 978-3-030-10472-6 (eBook), Springer Nature Switzerland AG. Pp. 63–89 https://doi.org/10.1007/978-3-030-10472-6_4 .

Santos-Trigo, M. (2020a). Problem-solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 686–693). Springer. https://doi.org/10.1007/978-3-030-15789-0 .

Santos-Trigo, M. (2020b). Prospective and practicing teachers and the use of digital technologies in mathematical problem-solving approaches. In S. Llinares and O. Chapman (Eds.), International handbook of mathematics teacher education , vol 2, pp: 163–195. Boston: Brill Sense, ISBN 978-90-04-41896-7.

Santos-Trigo, M. (Ed.). (2023). Trends and developments of mathematical problem-solving research to update and support the use of digital technologies in post-confinement learning spaces. InT. L. Toh (Eds.), Problem Posing and Problem Solving in Mathematics Education , pp: 7–32. Springer Nature Singapore. https://doi.org/10.1007/978-981-99-7205-0_2 .

Santos-Trigo, M., & Reyes-Martínez, I. (2019). High school prospective teachers’ problem-solving reasoning that involves the coordinated use of digital technologies. International Journal of Mathematical Education in Science and Technology , 50 (2), 182–201. https://doi.org/10.1080/0020739X.2018.1489075 .

Santos-Trigo, M., Barrera-Mora, F., & Camacho-Machín, M. (2021). Teachers’ use of technology affordances to contextualize and dynamically enrich and extend mathematical problem-solving strategies. Mathematics , 9 (8), 793. https://doi.org/10.3390/math9080793 .

Santos-Trigo, M., Reyes-Martínez, I., & Gómez-Arciga, A. (2022). A conceptual framework to structure remote learning scenarios: A digital wall as a reflective tool for students to develop mathematics problem-solving competencies. Int J Learning Technology , 27–52. https://doi.org/10.1504/IJLT.2022.123686 .

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grows (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). Macmillan.

Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM Mathematics Education, 52, pp: 1163–1175. https://doi.org/10.1007/s11858-020-01162-w .

Schoenfeld, A. H. (2022). Why are learning and teaching mathematics so difficult? In M. Danesi (Ed.), Handbook of cognitive mathematics (pp. 1–35). Switzerland. https://doi.org/10.1007/978-3-030-44982-7_10-1%23DOI .

Schoenfeld, A. H. (2023). A theory of teaching. In A. K. Praetorius, & C. Y. Charalambous (Eds.), Theorizing teaching (pp. 159–187). Springer. https://doi.org/10.1007/978-3-031-25613-4_6 .

Sinclair, N., & Ferrara, F. (2023). Towards a Socio-material Reframing of Mathematically Challenging Tasks. In R. Leikin (Ed.), Mathematical Challenges For All , Research in Mathematics Education, pp: 307–323. https://doi.org/10.1007/978-3-031-18868-8_16 .

Stake, R. E. (2000). Case studies. In N. K. Denzin, & Y. S. Lincoln (Eds.), Handbook of qualitative research (pp. 435–454). Sage.

Thurston, P. W. (1994). On proof and progress in mathematics. Bull Amer Math Soc , 30 (2), 161–177.

Toh, T. L., Santos-Trigo, M., Chua, P. H., Abdullah, N. A., & Zhang, D. (Eds.). (2023). Problem posing and problem solving in mathematics education: Internationa research and practice trends . Springer Nature Singpore. https://doi.org/10.1007/978-981-99-7205-0 .

Törner, G., Schoenfeld, A. H., & Reiss, K. M. (Eds.). (2007). Problem solving around the world: Summing up the state of the art [Special Issue]. ZDM — Mathematics Education , 39 (5–6). https://doi.org/10.1007/s11858-007-0053-0 .

Download references

Author information

Authors and affiliations.

Centre for Research and Advanced Studies, Mathematics Education Department, Mexico City, Mexico

Manuel Santos-Trigo

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Manuel Santos-Trigo .

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Santos-Trigo, M. Problem solving in mathematics education: tracing its foundations and current research-practice trends. ZDM Mathematics Education 56 , 211–222 (2024). https://doi.org/10.1007/s11858-024-01578-8

Download citation

Accepted : 18 April 2024

Published : 30 April 2024

Issue Date : May 2024

DOI : https://doi.org/10.1007/s11858-024-01578-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Mathematical problem solving
• Conceptual frameworks
• Digital and semiotic tools-
• Mathematical reasoning
• Mathematics education developments
• Digital technologies
• Find a journal
• Publish with us
• Track your research

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

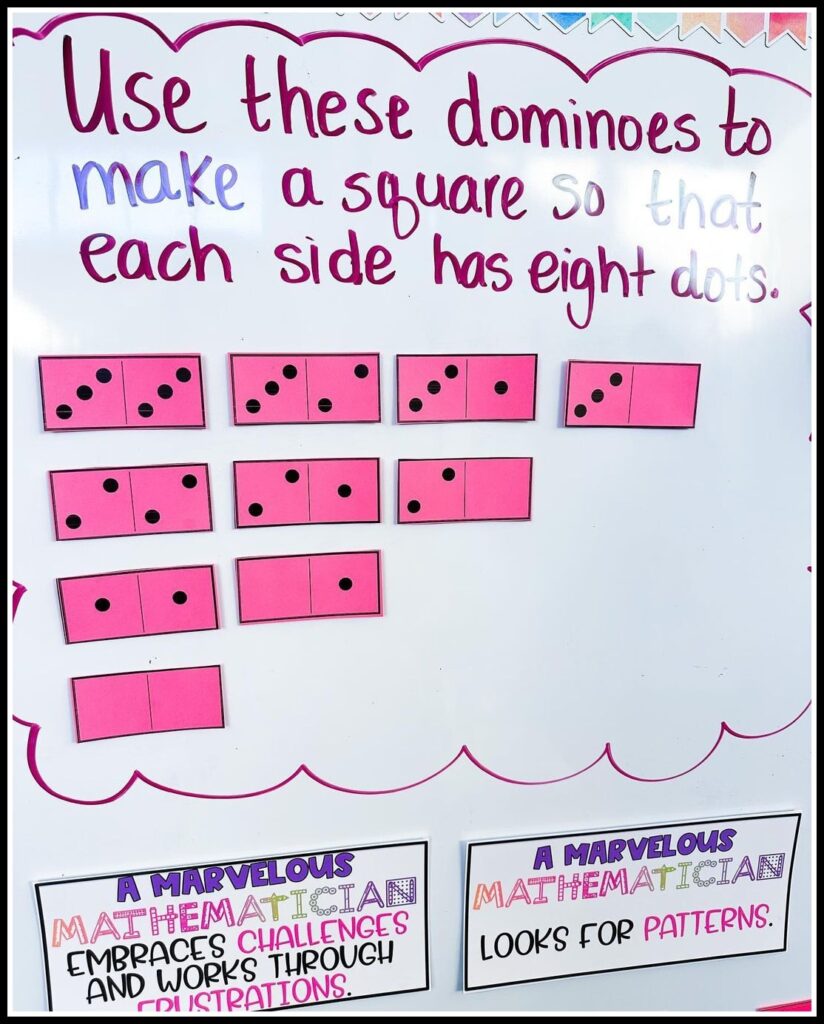
Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

We apologize for the inconvenience...

To ensure we keep this website safe, please can you confirm you are a human by ticking the box below.

If you are unable to complete the above request please contact us using the below link, providing a screenshot of your experience.

https://ioppublishing.org/contacts/