hybrid experimental method

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Design of Experiments with Sequential Randomizations on Multiple Timescales: The Hybrid Experimental Design

Inbal nahum-shani, john j dziak, hanna venera, angela f pfammatter, bonnie spring, walter dempsey.

• Author information
• Article notes
• Copyright and License information

Correspondence should be sent to: Inbal Nahum-Shani, Institute for Social Research, University of Michigan, [email protected]

Issue date 2024 Mar.

Psychological interventions, especially those leveraging mobile and wireless technologies, often include multiple components that are delivered and adapted on multiple timescales (e.g., coaching sessions adapted monthly based on clinical progress, combined with motivational messages from a mobile device adapted daily based on the person’s daily emotional state). The hybrid experimental design (HED) is a new experimental approach that enables researchers to answer scientific questions about the construction of psychological interventions in which components are delivered and adapted on different timescales. These designs involve sequential randomizations of study participants to intervention components, each at an appropriate timescale (e.g., monthly randomization to different intensities of coaching sessions and daily randomization to different forms of motivational messages). The goal of the current manuscript is twofold. The first is to highlight the flexibility of the HED by conceptualizing this experimental approach as a special form of a factorial design in which different factors are introduced at multiple timescales. We also discuss how the structure of the HED can vary depending on the scientific question(s) motivating the study. The second goal is to explain how data from various types of HEDs can be analyzed to answer a variety of scientific questions about the development of multi-component psychological interventions. For illustration we use a completed HED to inform the development of a technology-based weight loss intervention that integrates components that are delivered and adapted on multiple timescales.

Introduction

Advances in mobile and wireless technologies offer tremendous opportunities for building psychological interventions that include multiple components, where a component is defined as any aspect of the intervention that can be separated out for investigation (see Collins, 2018 ). In practice, decisions about the delivery of these components are often made on multiple timescales, as illustrated in the following three examples. First, in a technology-based weight loss intervention ( Pfammatter et al., 2019 ; Spring et al., 2020 ), a decision may be made every several weeks about whether to enhance the intensity of coaching sessions based on information about progress in weight loss. Additionally, every day a decision may be made about whether to deliver a motivational message via a mobile device to encourage self-monitoring of dietary intake, based on information about prior self-monitoring. Second, in an intervention designed to increase engagement in evidence-based tobacco cessation treatments ( Fernandez et al., 2020 ), a decision may be made weekly about whether or not to deliver a text message to encourage engagement in treatment, based on information about prior engagement; and after several months a decision may be made about whether or not to augment the text messages with brief counseling calls, based on information about treatment enrollment by that time. Third, in an intervention for young adults with type 1 diabetes ( Stanger et al., 2021 ), decisions may be made at the beginning of the program about whether or not to deliver two components–incentives to promote consistent daily adherence to goals, and online health coaching to teach effective problem solving—based on baseline diabetes indicators such as duration of diabetes and device use. In addition, decisions may be made daily about what type of feedback to deliver via a mobile device, based on prior adherence to self-monitoring blood glucose.

Investigators often have scientific questions about how to best guide decisions made on various timescales about intervention components. For example, is it better to start with low (vs. moderate) intensity coaching sessions, when motivational text messages are also being delivered daily? Is a daily text message more effective in promoting daily self-monitoring, when more intense coaching is being delivered? What combination of digital intervention components (e.g., mobile app, text messages, non-monetary digital incentives) should be offered initially, if four weeks later coaching sessions will be added for participants not showing sufficient weight loss?

Existing experimental designs can be used to empirically inform decisions about multiple intervention components that are introduced (a) at a single point in time (e.g., standard factorial designs; Collins, 2018 ); (b) sequentially over time, at relatively slow timescales, such as over several weeks or months (e.g., the Sequential Multiple Assignment Randomized Trial [SMART]; Lavori & Dawson, 2000 ; Murphy, 2005 ); or (c) sequentially over time, at relatively fast timescales, such as every day, several hours or minutes (e.g., the Micro-Randomized Trial [MRT]; Qian et al., 2022 ). However, although each of these experimental approaches is suitable for empirically informing intervention decisions on a particular timescale, they cannot be used to answer scientific questions about multiple intervention decisions that are made on different timescales.

The Hybrid Experimental Design (HED) is a new experimental approach developed explicitly to help investigators answer scientific questions about the selection and integration of intervention components that may be delivered on multiple timescales ( Nahum-Shani et al., 2022 ). The HED involves sequential randomizations on multiple timescales corresponding to the time period at which each component should be considered. The current manuscript conceptualizes the HED as a special form of a factorial design, wherein different factors are introduced on different timescales. We discuss how the flexibility of this experimental approach offers tremendous opportunities to address a variety of scientific questions about which components to deliver and under what conditions, where each component can be delivered on a different suitable timescale. While the HED is highly flexible and can take on many forms depending on the scientific questions motivating the study, we focus here on three types of HEDs: (1) those that integrate a standard factorial design and a SMART design (i.e., hybrid factorial-SMART); (2) those that integrate a standard factorial design and an MRT (i.e., hybrid factorial-MRT); and (3) those that integrate a SMART and an MRT (i.e., hybrid SMART-MRT). We discuss how data from these three types of HEDs can be analyzed to answer different scientific questions about the development of multi-component interventions. Throughout, we use examples based on a completed study to inform the development of a weight loss intervention that integrates components that are delivered and adapted on multiple timescales ( Pfammatter et al., 2019 ; Spring et al., 2020 ). The details of this study are modified here for illustrative purposes to demonstrate how different scientific questions require a different form of HED.

Motivation for HEDs

The HED is an experimental approach to help investigators develop intervention programs with multiple components that are sequenced and adapted on multiple timescales ( Nahum-Shani et al., 2022 ). The term adaptation here refers to the use of dynamic (ongoing) information about the individual to decide which component to deliver and when, with the goal of addressing an individual’s changing needs in the course of the intervention. For example, consider a weight loss intervention that begins with a mobile app alone, and then at week 2, if the individual does not lose a sufficient amount of weight the initial intervention is augmented with coaching; otherwise the individual continues with the initial intervention ( Pfammatter et al., 2019 ; Spring et al., 2020 ). This intervention decision making process involves adaptation because dynamic information about weight loss is used to decide whether or not to augment the mobile app with coaching. This information is often referred to as a “tailoring variable,” which is a term used to describe the information used in making intervention decisions ( Nahum-Shani et al., 2012a ; 2012b ). Note that the adaptation in this example occurs after 2 weeks because the goal is to address conditions (insufficient weight loss) that unfold over 2 weeks. The underlying assumption is that individuals who do not lose a sufficient amount of weight by week 2 are unlikely to achieve the long-term goal of the weight loss program (i.e., 5% weight loss by month 6) and hence need more support in the form of coaching in order to succeed ( Pfammatter et al., 2019 ; Spring et al., 2020 ). Those who lose sufficient weight by week 2 are likely to achieve the long-term goal of the program and hence do not need additional support in order to succeed. For these individuals, providing coaching at week 2 would be unnecessarily costly and burdensome. Hence, the goal of the adaptation is to increase the number of individuals who achieve long-term success (i.e., improving overall effectiveness of the intervention) while minimizing cost and burden (i.e., improving resource-efficiency of the intervention).

Advances in digital technologies offer tremendous opportunities to deliver and adapt interventions in real-time, real-world settings ( Koch et al., 2021 ; Nahum-Shani et al., 2015 ; Webb & Cohen, 2021 ). For example, the mobile app used in a weight loss program can leverage information collected via the mobile device to decide whether or not to send supportive prompts (e.g., via a push notification). Suppose that every day around mid-day, if information from the mobile device indicates that the individual did not self-monitor their dietary intake since waking up, a message is sent via the mobile device encouraging the individual to use the app to self-monitor their dietary intake; otherwise no message is sent. In this case, the adaptation occurs on a much faster timescale than the previous example because the goal is to address conditions (insufficient self-monitoring of dietary intake) that change relatively fast (on a daily basis). The underlying assumption is that insufficient self-monitoring on a given day would undermine the formation of a habit (defined as “a motor or cognitive routine that, once it is triggered, completes itself without conscious supervision”; Bernacer & Murillo, 2014 ) to self-monitor dietary intake and, in turn, undermine the likelihood of achieving the long-term goal of the weight loss program.

Although technology can be used to deliver support in a way that is accessible and relatively inexpensive, insufficient engagement remains a critical barrier to the effectiveness of digital interventions ( Nahum-Shani et al., 2022 ). Human delivery of interventions, such as coaching delivered by clinical staff, can be more engaging ( Ritterband et al., 2009 ; Schueller et al., 2017 ) but often more expensive and burdensome. Hence, integrating digital and human-delivered intervention components requires balancing effectiveness against scalability and sustainability ( Mohr et al., 2011 ; Schueller et al., 2017 ; Wentzel et al., 2016 ). Since digital and human-delivered components are typically delivered and adapted on different timescales—fast (e.g., every day, hour, minute) and slow (e.g., every few weeks or months), respectively—there is increasing need to develop multi-modality adaptive interventions (MADIs)—interventions in which digital and human-delivered intervention components are integrated and adapted on different timescales appropriate for each ( Nahum-Shani et al., 2022 ). The development of MADIs requires answering scientific questions about how to best integrate intervention components that are delivered and adapted on multiple timescales. In the next sections we provide examples of scientific questions about constructing effective MADIs and discuss how HEDs can be used to answer these questions.

Key Features of HEDs

The HED was designed to help investigators answer scientific questions about the construction of MADIs. The HED can be viewed as a flexible factorial design. A factorial design is a randomized trial involving two or more factors (i.e., independent variables that are manipulated systematically); possible levels of each factor are crossed with levels of the other factors to form a design with multiple experimental conditions to which study participants are randomized ( Collins, 2018 ). The resulting data can be used to estimate the main effect of each factor, as well as interactions between factors. The main effect is defined as the difference between the mean outcome at one level of the factor and the mean outcome at another level, averaging over the levels of all remaining factors ( Collins, 2018 ). Interactions capture the extent that the effect of one factor varies by the levels of other factors. For example, a two-way interaction can be defined as half the difference between two effects: (1) the effect of a particular factor (i.e., the difference in the mean outcome between the two levels of the factor), at one level of the other factor, averaging over the levels of all remaining factors; and (2) the effect of that particular factor, at the second level of the other factor, averaging over the levels of all remaining factors (for details, see Collins, 2018 ).

The extant literature demonstrates the efficiency of various types of factorial designs in answering scientific questions about the selection of intervention components (for example, see Chakraborty et al., 2009 ; Collins et al., 2005 ; Nahum-Shani & Dziak, 2018 ; Nahum-Shani et al., 2018 ; Nair et al., 2008 ). Specifically, factorial designs enable investigators to combine multiple experimental cells in different ways, such that outcome data from each study participant can be used to test more than one main effect, thereby answering multiple scientific questions about the selection of intervention components. Collins and colleagues (2009) described this as the “recycling” of study participants and discussed the efficiency of this approach for estimating both main effects and interactions.

Building on this literature, the HED can be conceptualized as a flexible factorial design wherein subjects are sequentially randomized to factors on multiple timescales. Each factor corresponds to an intervention component; participants are randomized to each factor at decision points relevant to that component, namely at time points at which decisions should be made in practice about whether and how to deliver this component. Further, each factor is matched with a primary outcome that measures changes at a suitable timescale. The structure of the HED should match the scientific questions of interest and the relevant timescale for each component under investigation.

HED Examples

In this section, we discuss three types of HEDs that can be used to address different sets of scientific questions. For each HED, we discuss how the data can be analyzed to address the pre-specified scientific questions.

Hybrid Factorial-SMART

Suppose investigators are motivated to answer the following questions about the development of a weight loss intervention that integrates human-delivered and digitally delivered components. These questions concern two decision points: the beginning of the program and two weeks later. Specifically, at the beginning of the program investigators would like to know if it is beneficial (in terms of weight loss at month 6), (Q1) to offer a mobile app that includes on-demand weight loss strategies and resources (App); and/or (Q2) to offer weekly coaching (Coaching). Further, investigators would like to know (Q3) whether individuals who show early signs of non-response at week 2 would benefit from adding meal replacement (Meal).

To answer these questions, the investigators may consider an experiment with three factors, one factor for each component. Using italicized abbreviations to represent experimental factors, App refers to the factor corresponding to the mobile app, Coaching refers to the factor corresponding to weekly coaching sessions, and Meal refers to the factor corresponding to meal replacement. Each factor will have two levels: On and Off. Note that in practice, decisions regarding the components App and Coaching should be made at the beginning of the program. Hence, study participants should be randomized to the corresponding factors App and Coaching before beginning the program. The decision regarding Meal should be made at week 2. Hence, study participants should be randomized to the corresponding factor Meal at week 2. Also notice that the question regarding the Meal component only concerns non-responders at week 2. Hence the randomization to the factor Meal should be restricted to non-responders; that is, only non-responders at week 2 should be randomized to this factor.

The experimental design in Figure 1a can provide data for addressing questions Q1–Q3. At the beginning of the study, participants are randomized to one of four experimental options resulting from crossing the levels of the two factors App and Coaching . This is similar to a standard 2×2 factorial experiment. Then, at week 2, non-responders are randomized again to the two levels of Meal , whereas responders continue with their assigned initial intervention. Thus, there are three possible experimental options at week 2, two for non-responders and one for responders. Overall this design integrates a standard 2×2 factorial experiment with a Sequential, Multiple Assignment, Randomized trial (SMART; Lavori & Dawson, 2000 ; Murphy, 2005 ).

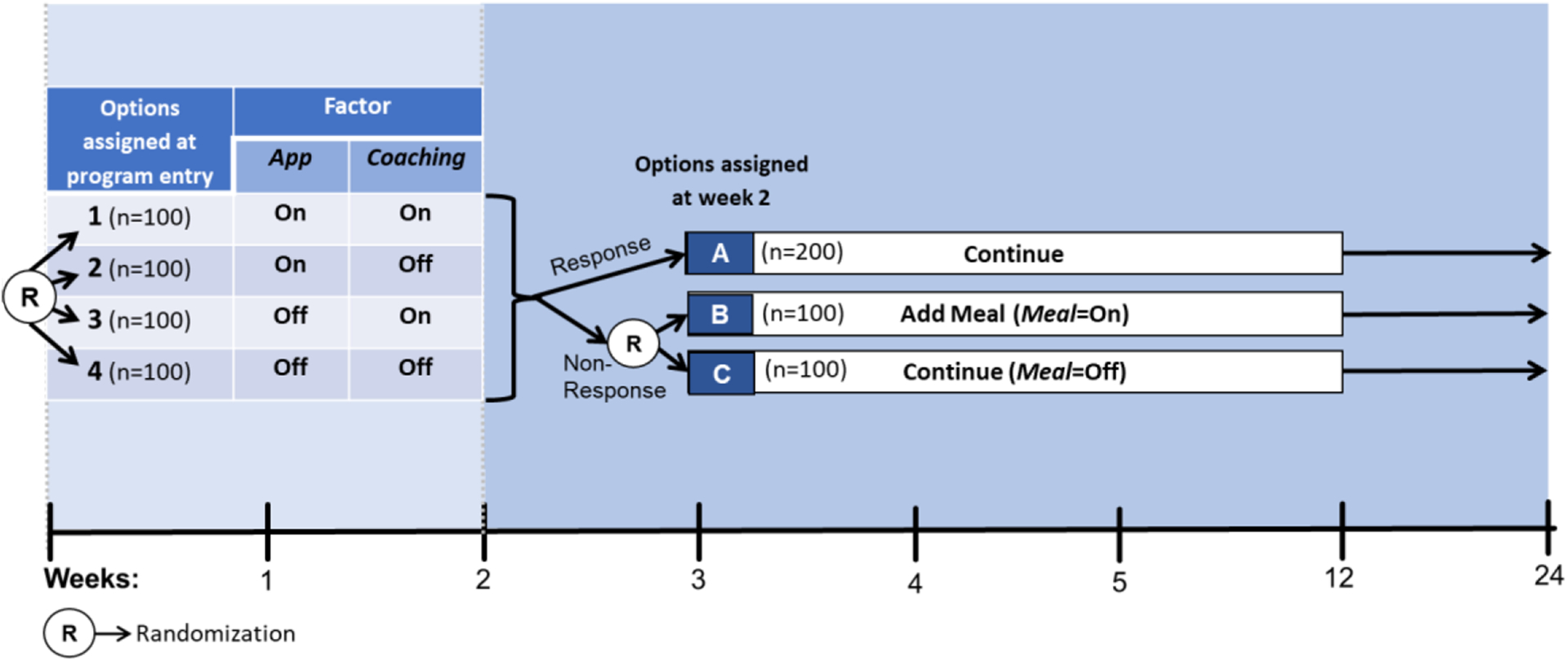
An Example Hybrid Factorial-SMART

A SMART is itself already a form of factorial design ( Nahum-Shani et al., 2012a ) involving sequential randomizations to experimental factors. In a prototypical SMART, there are two decision points at which individuals are randomly assigned to factors, but random assignment at the second decision point is restricted to non-responders ( Ghosh et al., 2020 ; Nahum-Shani et al., 2020a ), as in the current design. This restriction is typically informed by prior empirical evidence or practical considerations indicating that individuals who show early signs of response are likely to benefit from continuing with the initial intervention, whereas those showing early signs of non-response are unlikely to benefit and may require treatment modification in order to succeed ( Nahum-Shani & Almirall, 2019 ). The randomization of non-responders at week 2 in the current example is designed to investigate whether this subgroup would benefit from adding meal replacement (Meal).

Suppose that 400 individuals enter the study (for simplicity, throughout we assume no attrition) and are randomized at program entry with equal probability (0.25) to each of the four experimental options 1–4 in Figure 1a (i.e., n =100 participants in each option). Then, suppose that at week 2, 50% of the participants are classified as responders ( n =200) and continue with the initial intervention (option A). Those classified as non-responders ( n =200) are re-randomized with equal probability (0.50) to either add meal replacement (option B; n =100) or not (option C; n =100).

The sequential randomization in Figure 1a leads to 12 experimental cells, which are detailed in Figure 1b . For example, participants who start with both Coaching and App (option 1 at program entry) and then show early signs of response and thus continue with the initial intervention (option A at week 2) are considered part of experimental cell 1→A; those who started with both Coaching and App (option 1 at program entry) and then show early signs of non-response and are assigned to add Meal (option B at week 2) are considered part of experimental cell 1→B. As we discuss below, similar to a standard factorial design, the goal here is not to compare these individual cells, but rather to combine multiple cells in different ways to answer multiple scientific questions about the selection of intervention components ( Collins, 2018 ).

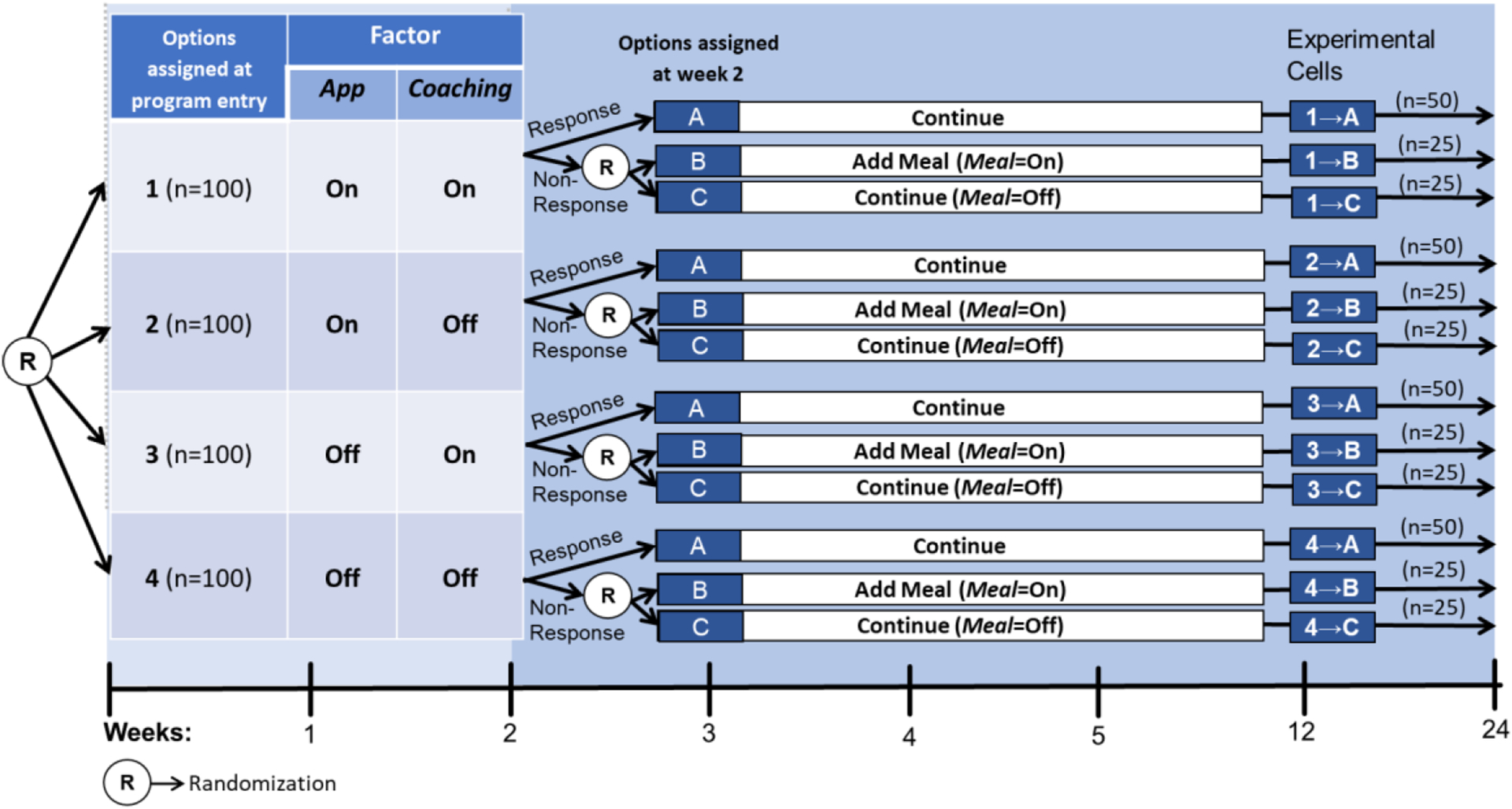
Experimental Cells in The Example Hybrid Factorial-SMART

Further, similar to a prototypical SMART design ( Nahum-Shani et al., 2020a ), several adaptive interventions are embedded in this trial. An embedded adaptive intervention is a sequence of decision rules that is included in the trial by design. It specifies which components to deliver (and for whom) at each decision point (see Nahum-Shani & Almirall, 2019 ; Nahum-Shani et al., 2022 ). Here, there are eight embedded adaptive interventions, which are described in Table 1 ; each is represented by 2 of the 12 experimental cells in Figure 1b , with some adaptive interventions sharing cells. Next, we describe how data from this hypothetical study can be analyzed to answer questions Q1–Q3, as well as other, more exploratory questions.

Adaptive interventions embedded in the hybrid factorial-SMART in Figure 1

Data analytic approach for hybrid factorial-SMART.

In the current example the primary outcome of interest is weight loss measured at the month 6 follow up. Data from an illustrative (hypothetical) experimental design shown in Figure 1 can be used to answer the three motivating questions outlined above, about the inclusion of App and Coaching at the beginning of the program and the inclusion of Meal for non-responders at week 2. This can be done by testing the main effect of each corresponding factor. Specifically, using data from the HED in Figure 1 , the main effect of App can be estimated by comparing the mean outcome across all the cells in which App was set to On (the 6 cells starting with options 1 and 2; n =200; Figure 1 ) to the mean outcome across all the cells in which App was set to Off (the 6 cells starting with options 3 or 4; n =200; Figure 1 ). Similarly, the main effect of Coaching can be estimated by comparing the 6 cells starting with options 1 and 3 ( n =200) to the 6 cells starting with options 2 and 4 ( n =200). Notice that both main effects are estimated by using outcome information from the entire sample ( N =400), and they average over the factor Meal and the response status.

Next, the main effect of adding meal replacement to non-responders ( Meal ) can be estimated in two ways: the first is conditional on response status, and the second is marginal (i.e., averaged over response status). The conditional approach would be restricted to non-responders and would involve comparing the mean outcome of all non-responders who were offered Meal at week 2 (i.e., the 4 cells involving option B in Figure 1b ; n =100) with the mean outcome of all non-responders who were not offered Meal at week 2 (i.e., the 4 cells involving option C in Figure 1b ; n =100). Notice that this main effect is estimated by using outcome information from the entire sample of non-responders ( n =200), but it only includes non-responders. Thus, this main effect is averaged over the factors assigned at program entry, but it is conditional on response status. Alternatively, the marginal approach would involve comparing (a) the mean outcome across all the cells of responders (i.e., the 4 cells involving option A in Figure 1b ; n =200) and non-responders who were offered Meal at week 2 (i.e., the 4 cells involving option B in Figure 1b ; n =100) with (b) the mean outcome across all the cells of responders (i.e., the 4 cells involving option A in Figure 1b ; n =200) and non-responders who were not offered Meal at week 2 (i.e., the 4 cells involving option C in Figure 1b ; n =100). Notice that this main effect is estimated by using outcome information from the entire sample, including responders and non-responders. Thus, this definition of the main effect is averaging over the factors assigned at program entry and response status. The conditional effect will generally be a larger quantity than the marginal effect, because Meal has no effect on responders, and therefore the marginal effect is a weighted average of the (potentially nonzero) effect on non-responders and the (necessarily zero) effect on responders. However, as we discuss below, this does not matter for testing purposes. Below, we discuss modeling and estimation considerations in using data from a hybrid factorial-SMART to estimate main effects, as well as interactions between factors.

Proposed model and estimands.

Let Z 11 and Z 12 be the randomized factors at program entry (here, App and Coaching , respectively), both coded +1 when the corresponding component is set to On and −1 when it is set to Off, and let Z 21 be the randomized factor for non-responders at week 2 (here, Meal ), also coded +1 for On and −1 for Off. Let X 0 be a vector of control covariates measured prior to first-stage randomization (and included in the regression models as mean-centered covariates). The following is a relatively simple model that can be fitted to answer questions about the main effect of each component and interactions between them:

Throughout we assume for simplicity that the outcome is continuous, but all the models discussed in this manuscript can be extended to other types of outcomes (e.g., binary and count) by using the appropriate link function.

Table 2 summarizes how the coefficients in Model (1) can be used to answer a variety of scientific questions about the main effect of each component and the interactions between them. For example, consider Q1 above, which concerns whether at program entry it is beneficial (in terms of weight loss at month 6), to offer the App (vs. no App). Based on Model (1) , E ( Y | Z 11 = 1) = θ 1 is the average weight loss for those who were offered App at program entry, averaging over response status and the other factors (i.e., Z 12 and Z 21 ). Similarly, E ( Y | Z 11 = −1) = − θ 1 is the average weight loss for those who were not offered App, and so ( E ( Y | Z 11 = 1) − E ( Y | Z 11 = −1)) = 2 θ 1 is the main effect of App . This main effect is the average difference in weight loss between those who were offered the app and those who were not offered the app at program entry, averaging over response status and the other factors. Similarly, 2 θ 2 can be used to estimate the main effect of Coaching , which is the focus of Q2.

Scientific questions and model parameters for a hybrid factorial-SMART

Further, 2 θ 4 can be used to answer Q3, which concerns whether it would be beneficial to add (vs. not add) meal replacement for individuals who show early signs of non-response at week 2; this quantity represents the main effect of Meal , averaging over the other factors and response status. This main effect is based on the marginal approach discussed above, which averages over response status. Estimating the effect of Meal only among non-responders (i.e., conditional on response status) would require rescaling the quantity 2 θ 4 by a factor of 1/(1 − r ), where r is the response rate. The magnitude of this conditional effect will generally be larger than the marginal effect, but the statistical tests are equivalent because both the estimand and standard error would be rescaled by the same factor, leading to the same conclusions (e.g., same p -value).

The coefficients in Model (1) can also be used to answer scientific questions about how well the components work together. For example, is the app more beneficial with or without coaching? The interaction between the two initial factors Z 11 and Z 12 can be used to answer this question. Specifically, this interaction represents the difference between two “simple effects”: (1) the effect of App when Coaching is set to On, averaging over response status and Z 21 , namely ( E ( Y | Z 11 = 1, Z 12 = 1) − E ( Y | Z 11 = −1, Z 12 = 1)) = 2 θ 3 ; and (2) the effect of App when Coaching is set to Off, averaging over response status and Z 21 , namely ( E ( Y | Z 11 = 1, Z 12 = −1) − E ( Y | Z 11 = −1, Z 12 = −1)) = −2 θ 3 . The difference between these two simple effects is 4 θ 3 ; rescaling this quantity by ½ for comparability (see Collins et al., 2018 ), 2 θ 3 represents the interaction between App and Coaching .

Next, consider another scientific question about how well components that are offered at different decision points work together: Does the overall benefit of the App (in terms of month 6 weight loss) change based on whether Meal is offered to non-responders at week 2? The marginal interaction between Z 11 and Z 21 can be used to answer this question. This interaction represents the difference between two “simple effects”: (1) the effect of App when Meal is set to On among non-responders, averaging over response status and Z 12 , namely ( E ( Y | Z 11 = 1, Z 21 = 1) − E ( Y | Z 11 = −1, Z 21 = 1)) = 2 θ 5 ; and (2) the corresponding effect when Meal is set to Off among non-responders, namely −2 θ 5 . The difference between these two simple effects is 4 θ 5 ; rescaling this quantity by ½ for comparability (see Collins et al., 2018 ), 2 θ 5 represents the interaction between App and Meal , averaging over response status and Coaching .

Finally, linear combinations of the coefficients in Model 1 can also be used to compare adaptive interventions that are embedded in the design. The contrast between expected population outcomes under embedded adaptive interventions ( z 11 , z 12 , z 21 ) and ( z 11 ′ , z 12 ′ , z 21 ′ ) is

For example, consider the contrast between (+1, 1,1) and (−1, 1,1), which can be quantified based on Model 1 as follows: μ (+1, 1,1) − μ (−1, 1,1) = 2 θ 1 + 2 θ 3 +2 θ 5 + 2 θ 7 , where μ is the expected mean outcome if everyone in the population was offered a given adaptive intervention. This is a contrast between two embedded adaptive interventions, both offering Coaching initially and then offering Meal replacement to non-responders (responders continue with the initial intervention), but the former also offers App initially (adaptive intervention #1 in Table 1 ), whereas the later does not (adaptive intervention #5 in Table 1 ).

Estimation.

The Weight and Replicate (W&R) data analysis method ( Dziak et al., 2019 ; Nahum-Shani et al., 2020a ; Nahum-Shani et al., 2012a ) can be used to estimate the parameters in Model (1) . Appendix A of Nahum-Shani et al., (2012a) provides a technical explanation of this approach and demonstrates that the estimators are unbiased in large samples. W&R was developed to address two challenges related to estimation in a prototypical SMART setting; these challenges are also relevant to the hybrid factorial-SMART in Figure 1 . First, responders are not re-randomized to the second-stage factor ( Meal ); instead they are offered a fixed intervention option (continue with the initial intervention). Thus, the value of Z 21 for responders is not specified (by design). Further, each responder provides data that are consistent with two of the eight embedded adaptive interventions in Table 1 . For example, responders to App alone (i.e., those in Cell 2→A) provide data that are consistent with both embedded adaptive intervention #3 ( Table 1 ) and embedded adaptive intervention #4 ( Table 1 ). Thus, the value of Z 21 should be specified in such a way that enables outcome data from responders to be used to estimate the mean outcome under both embedded adaptive interventions. W&R employs replication of responders’ data to address this challenge.

Specifically, each row in the dataset that pertains to a responder is duplicated, using the same values for all variables (including Y ), except for Z 21 . One of the duplicated rows is assigned Z 21 = 1, while the other is assigned Z 21 = −1. The number of rows in the new, re-structured dataset will be N + ∑ i = 1 N R i , where N is the actual number of original participants before replication, and R i indicates whether ( R i = 1) or not ( R i = 0) the i th participant was classified as a responder to first-stage components. It is important to note that W&R does not assume that the true data set is of size N + ∑ i = 1 N R i ; rather, the method correctly assumes that the sample size is N for purposes of calculating standard errors (see Nahum-Shani et al., 2020a ; Nahum-Shani et al., 2012a ).

Second, non-responders are re-randomized to second-stage intervention options, while responders are not re-randomized (in Figure 1 they continue with the option assigned at program entry). Therefore, outcome information from non-responders is underrepresented in the sample mean under a particular embedded adaptive intervention; this underrepresentation occurs by design. Correspondingly, the probability of being assigned to a sequence of components that is consistent with a particular embedded adaptive intervention is lower for non-responders than responders. In Figure 1 this probability is 0.25 for non-responders (because they were randomized twice with probability 0.5 each time) and 0.5 for responders (because they were randomized only once with probability 0.5). Because of this imbalance, and because response status is expected to be associated with the outcome, taking a naïve average of Y for all individuals consistent with a specific embedded adaptive intervention likely leads to bias ( Orellana et al., 2010 ; Robins et al., 2008 ). To restore balance, W&R employs weights that are proportional to the inverse of the probability of treatment assignment. In the case of the hybrid factorial-SMART in Figure 1 , responders’ observations are assigned the weight W =2 (the inverse of 0.5), and non-responders’ observations are assigned the weight W =4 (the inverse of 0.25). These weights are often referred to as “known weights” because they are based on the design’s known treatment assignment probabilities. Alternatively, these weights can be estimated based on data from the SMART, with the potential to improve the estimator’s efficiency (i.e., achieve smaller standard errors; Brumback, 2009 ; Hernan et al., 2002 ; Hirano et al., 2003 ; Nahum-Shani et al., 2020a ).

With the data replicated and weighted as described above, Model (1) can be estimated by using standard software (e.g., SAS, R) with robust (sandwich) standard errors (e.g., in SAS GENMOD procedures). Nahum-Shani et al (2012a) provide a detailed justification for using robust standard errors in this setting.

Hybrid Factorial-MRT

Suppose investigators are motivated to answer the following questions about the development of a weight loss intervention that offers a mobile app to participants at the beginning of the program. The first two questions concern whether or not, at the beginning of the program, the app should be augmented with other components. Specifically, at the beginning of the program is it beneficial (in terms of weight loss at month 6), to (Q4) augment the app with coaching sessions; and/or (Q5) augment the app with meal replacement. The third question concerns the delivery of a prompt to encourage monitoring of that day’s dietary intake. Specifically, (Q6) is it beneficial (in terms of increasing self-monitoring of dietary intake in the next 12 hours) to deliver a mobile-based prompt (via a push notification) at mid-day? Note that Q4 and Q5 focus on components that can be delivered at a single decision point (here, at program entry). On the other hand, Q6 concerns a time-varying component—a component that may or may not be delivered at several decision points during the course of the intervention (i.e., the decision whether or not to deliver this component is made repeatedly during the intervention).

To answer these questions, the investigators may consider an experiment with three factors, one factor for each component. Here, Add Coaching refers to the factor corresponding to augmenting the app with coaching throughout the study, Add Meal refers to the factor corresponding to augmenting the app with meal replacement throughout the study, and Prompt refers to the factor corresponding to delivering a prompt to motivate self-monitoring on a given day. Each factor will have two levels: On and Off. Since decisions regarding the components Add Coaching and Add Meal should be made at the beginning of the program, study participants should be randomized to the corresponding factors Add Coaching and Add Meal at a single decision point – just prior to beginning the program. However, decisions regarding the delivery of the component Prompt can be made repeatedly, every day. Hence, study participants should be randomized to the corresponding factor Prompt at multiple decision points (i.e., daily at mid-day). We use the term “time-varying factor” to refer to a factor to which participants can be randomly assigned at multiple decision points during the study.

Note that Q4 and Q5 (about the benefits of augmenting the app with coaching and meal replacement at program entry) focus on a distal outcome—weight loss at month 6, whereas Q6 (about the benefits of delivering a mobile-based prompt at mid-day) focuses on a proximal outcome—self-monitoring of dietary intake in the next 12 hours. The focus of Q6 on a proximal outcome is motivated by the timescale at which the component of interest can be delivered (every day) and the timescale at which it is likely to impact behavior change (the delivery of a mobile-based prompt on a given day is likely to encourage relatively near-term self-monitoring behaviors).

The experimental design in Figure 2 can provide data for addressing questions Q4–Q6. At the beginning of the study, participants are randomized to one of four experimental options resulting from crossing the levels of the two factors Add Coaching and Add Meal . In addition, throughout the first 12 weeks, individuals are randomized daily to the two levels of the factor Prompt . This design integrates a standard 2×2 factorial experiment with a micro-randomized trial (MRT; Liao et al., 2016 ; Qian et al., 2022 ). An MRT is a form of a factorial design ( Walton et al., 2018 ) involving rapid sequential randomization to experimental factors. Specifically, randomizations to experimental factors occur frequently, and the time interval between randomizations is relatively short (e.g., hourly, daily). An MRT with a single factor that can take either of two levels (e.g., prompt vs. no prompt) at each randomization time can be viewed as a factorial design with 2 K potential experimental cells, where K is the number of decision points in which randomizations take place. However, similar to a standard factorial design, the primary scientific focus is not on comparing individual cells, but rather on the average main effect of the factor on a proximal outcome (i.e., proximal main effect), which, as we explain below, can be estimated by pooling outcome data across all K decision points and N individuals.

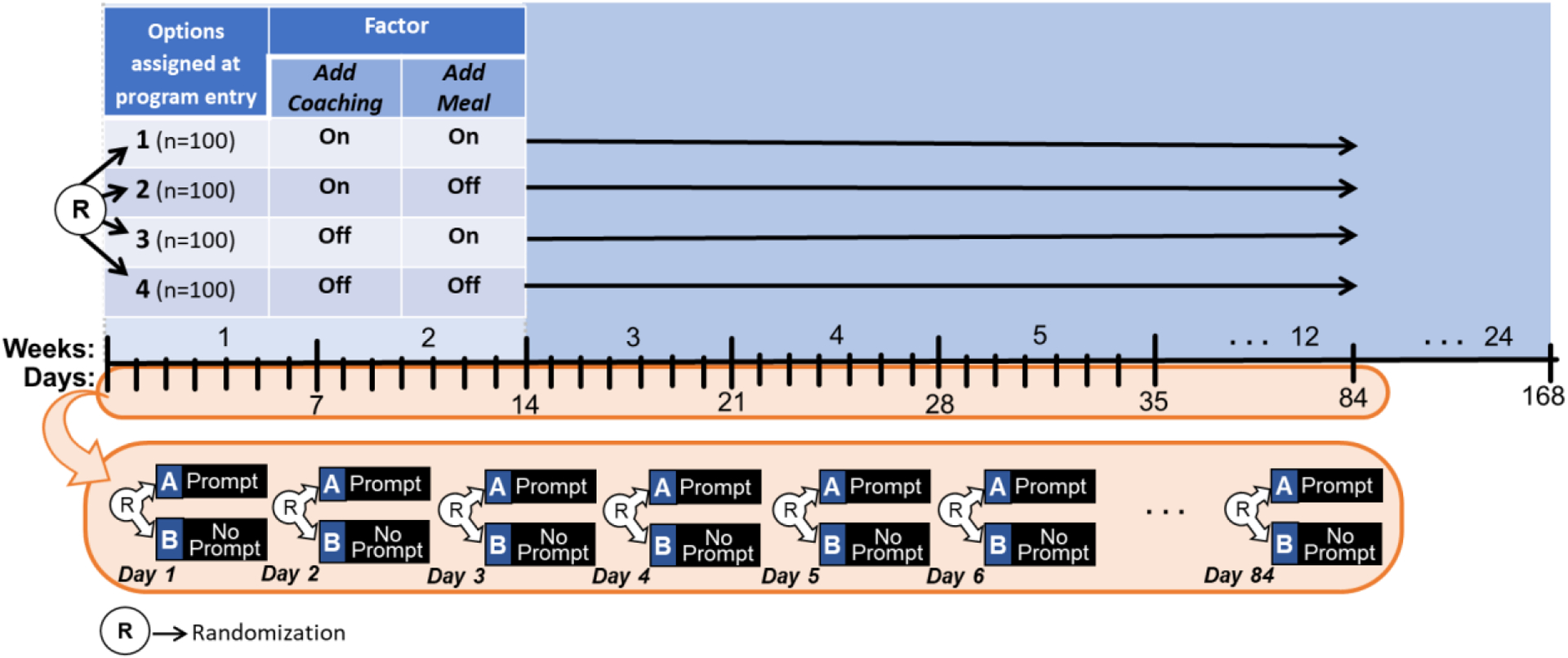
An Example Hybrid Factorial-MRT

Suppose that 400 individuals enter the study and are randomized initially with equal probability (0.25) to each of the four conditions 1–4 in Figure 2 (i.e., n =100 participants in each condition). Then, suppose that every day, at mid-day, each individual is randomized with equal probability (0.5) to each of the two levels of Prompt , that is, to either a prompt (condition A; n =100) or no prompt (condition B; n =100). Similar to a standard factorial design, the goal here is not to compare the cells resulting from crossing the levels of all factors at all decision points that involve randomization, but rather to combine multiple cells in different ways to answer multiple scientific questions about the selection of intervention components ( Collins, 2018 ). Below, we discuss how data from this hybrid factorial-MRT design can be used to answer questions Q4–Q6.

Data analytic approach for hybrid factorial-MRT.

Recall that in the current example, questions Q4 and Q5 (about the benefits of adding coaching to the app and adding meal replacement to the app) concern a distal outcome—weight loss measured at the month 6 follow up. Data from the experimental design in Figure 2 can be used to answer these questions by testing the distal main effect of each corresponding factor. Recall that when a factor has two levels, the main effect of this factor can be defined as the difference between the mean outcome at one level of this factor and the mean outcome at the other level of this factor, averaging over the levels of the other factors. Thus, using data from the HED in Figure 2 , the main effect of Add Coaching can be estimated by comparing the mean outcome across all the cells in which Add Coaching was set to On (i.e., those starting with options 1 and 2 in Figure 2 ; n =200) to the mean outcome across all the cells in which Add Coaching was set to Off (i.e., those starting with options 3 or 4 in Figure 2 ; n =200). Similarly, the main effect of Add Meal can be estimated by comparing the mean outcome across all the cells in which Add Meal was set to On (i.e., those starting with options 1 and 3 in Figure 2 ; n =200) to the mean outcome across the cells in which Add Meal was set to Off (i.e., those starting with options 2 and 4 in Figure 2 ; n =200). Note that both main effects also average over the levels of the factor Prompt at each decision point (1 through 84), and both are estimated by using outcome information from the entire sample ( N =400).

Next, recall that Q6, about the benefits of delivering a prompt to encourage daily self-monitoring, concerns a proximal outcome—self-monitoring of dietary intake over the next 12 hours. This proximal outcome is assessed following each randomization. The main effect of the time-varying factor Prompt can be estimated by comparing the mean outcome across all days in which a prompt was delivered (i.e., option A which was initiated, on average, on half of the days) to the mean outcome across all days in which a prompt was not delivered (i.e., option B which was initiated, on average, on half of the days). This difference is estimated by pooling data not only across all decision points in the trial, but also across all study participants ( Qian et al., 2022 ). That is, proximal outcome data from participants in all four initial experimental options 1–4 ( N =400) can be used to estimate this effect, which represents the (causal) main effect of Prompt in terms of the proximal outcome, averaging over the other factors and all decision points in the trial.

Notably, in a standard factorial design, the focus is on estimating the distal main effect of a factor, namely the main effect of a given factor on an outcome that is typically measured at a single (or a few) fixed later end-points (e.g., an end-of-study follow up), averaging over the levels of the other factors in the design ( Collins et al., 2009 ). However, in standard MRTs the main focus is on estimating the average proximal main effect of a factor, namely the main effect of a given factor on an outcome that is measured rapidly, following each decision point, averaging over all decision points (and individuals) in the trial ( Qian et al., 2022 ). By integrating features from a standard factorial design and a standard MRT, a hybrid factorial-MRT provides data that can be used to estimate both distal main effects and proximal main effects, averaging over the levels of the other factors in the experiment, as well as over the decision points in the experiment. Below, we discuss modeling and estimation considerations in using data from a hybrid factorial-MRT to estimate main effects as well as interactions between factors.

Let Z 11 and Z 12 be the two factors randomized at program entry (here, Add Coaching and Add Meal , respectively), both coded +1 for On and −1 for Off. Let t = 1, … , T be the decision points at which individuals are micro-randomized; in the current example, there is one decision point per day over 12 weeks: T = 7 × 12 = 84 days. Let A i , t represent the micro-randomized factor (here, Prompt ) for individual i , at time t , with levels +1 for On (i.e., prompt) and −1 for Off (i.e., no prompt). Let Y i * represent the distal outcome (here, weight loss at month 6) for individual i and let Y i , t +Δ represent the proximal outcome (self-monitoring dietary intake) for individual i at time t + Δ. In the current example, Δ represents the next 12 hours following decision point t ; that is, Δ does not represent a separate model parameter, but rather some pre-specified time Δ that comes after the assignment of A i , t but before the assignment of A i , t +1 . Thus, A i , t may causally affect Y i , t +Δ . As before, let X 0 be a vector of control covariates measured prior to program entry randomizations and included in the regression models as mean-centered covariates. The following model can be estimated to answer questions about the distal main effect (Q4 and Q5 outlined above) of the factors assigned at program entry and the interactions between them:

This model is marginal over A ¯ i , which is the average of the factor Prompt (i.e., the rate of prompt delivery) across all decision points for individual i . Alternatively, the subject-specific average of the factor Prompt can be included in the model as follows:

Table 3 summarizes how the coefficients in Model (2) can be used to answer a variety of scientific questions about the distal main effects of the factors assigned at program entry, the interactions between them, and their interactions with the time-varying factor. For example, consider Q4: whether at the beginning of the program it is beneficial (in terms of weight loss at month 6) to add (vs. not add) coaching. Assuming participants are assigned to each level of Z 11 , Z 12 and A with equal probability (0.5), then E ( Z 11 ) = 0, E ( Z 12 ) = 0, E ( Z 11 Z 12 ) = 0, and E ( A ¯ ) = 0 . Therefore, based on Model (2) , E ( E ( Y *| Z 11 = 1) − E ( Y *| Z 11 = −1)) = 2 θ 1 is the main effect of Add Coaching , namely the average difference in weight loss between those who were offered coaching and those who were not offered coaching at the beginning of the program, averaging over the other factor that was assigned at program entry ( Add Meal ) and the time-varying factor ( Prompt ). Similarly, E ( E ( Y *| Z 12 = 1) − E ( Y *| Z 12 = −1)) = 2 θ 2 can be used to answer Q5, which concerns whether at the beginning of the program it is beneficial to add (vs. not add) meal replacement. This quantity represents the main effect of Add Meal , averaging over the other factor that was assigned at program entry ( Add Coaching ) and the time-varying factor (i.e., Prompt ).

Scientific questions about distal effects and model parameters for a hybrid factorial-MRT

The parameters in Model (2) can be used to answer other scientific questions about the interactions between the factors assigned at program entry and the time-varying factor in terms of the distal outcome. For example, consider Question D from Table 3 : Does the effect of (i.e., difference between) adding (vs. not adding) coaching at the beginning of the program on the distal outcome (weight loss by month 6) vary by the rate of prompt delivery? This question concerns the interaction between a factor that was assigned at program entry and a time-varying factor that was assigned daily, in relation to the distal outcome. The randomizations to the time-varying factor Prompt (prompt vs. no prompt) with ½ probability each day lead to slightly different total numbers of prompts delivered per participant. Although the values of this distribution may be tightly clustered around the mean (due to the law of large numbers), they do differ slightly by random chance from participant to participant. Based on Model (2) , subtracting the conditional effects of the factor Add Coaching on the distal outcome, given two different A ¯ values of interest, can be interpreted as an interaction. For example, if A ¯ = 0.4 , then the conditional effect of Add Coaching is ( E ( Y * ∣ Z 11 = + 1 , A ¯ = . 4 ) − E ( Y * ∣ Z 11 = − 1 , A ¯ = . 4 ) ) = ( θ 1 + 0.4 θ 5 ) − ( − θ 1 − 0.4 θ 5 ) = 2 ( θ 1 + 0.4 θ 5 ) , and if A ¯ = 0.1 , then the conditional effect is 2( θ 1 + 0.1 θ 5 ). The difference between these two conditional effects is 2 × 0.3 θ 5 . Rescaling this quantity by ½ ( Collins et al., 2018 ), 0.3 θ 5 represents the interaction between Add Coaching and the specified difference in rate of prompt delivery. As before, this interaction would be estimated by using data across all study participants and across all decision points.

Next, the following model can be estimated to answer questions about the proximal main effect of the time-varying factor ( Prompt ) and the interactions between this factor and the two factors assigned at program entry ( Add Coaching and Add Meal ).

Note that a richer model could be specified to investigate whether the proximal effects are time-varying. For example, linearly time-varying effects could be explored using the model

where t is time in the study. Thus, the proximal effect of A i , t , averaging over Z i 11 and Z i 12 , is γ 0 + γ 1 t . The initial effect is γ 0 , but afterwards the effect can increase or decrease. Other kinds of trajectories, such as exponential decay or quadratic, could alternatively be used for more flexibility in modeling the change in effects.

Table 4 summarizes how the coefficients in Model (3) can be used to answer a variety of scientific questions about the proximal main effect of the time-varying component, as well as other questions about the interaction between this component and the two program entry components. For example, consider Q6, which concerns whether it is beneficial (in terms of self-monitoring of dietary intake in the next 12 hours) to deliver a prompt at mid-day. This question concerns the main effect of the time-varying factor Prompt on the proximal outcome, averaging over the other factors and all decision points in the trial. Under Model (3) , E ( Y i , t + Δ ∣ A i t = + 1 ) − E ( Y i , t + Δ ∣ A i t = − 1 ) = 2 γ 0 is the proximal main effect of Prompt , averaging over the other factors and decision points in the trial.

Scientific questions about proximal effects and model parameters for a hybrid factorial-MRT

The parameters in Model (3) can also be used to answer scientific questions about the interaction between the time-varying factor and other factors in terms of the proximal outcome. For example, consider Question B from Table 4 : Does the effect of Prompt (i.e., the difference between delivering vs. not delivering a prompt) on the proximal outcome vary by whether or not coaching was initiated at program entry? This question concerns the interaction between the time-varying factor and a factor that was assigned at program entry in relation to the proximal outcome. Using Model 3 ,

Rescaling this quantity by ½ ( Collins et al., 2018 ), 2 γ 1 represents the interaction between Prompt and Add Coaching , averaging over Add Meal and all the decision points in the trial. Other scientific questions and their associated Model (3) parameters are presented in Table 4 .

Model (2) can be estimated using standard regression procedures that are included in standard statistical software (e.g., SAS, R). Model (3) can be estimated with repeated measurement regression procedures in standard statistical software, such as Generalized Estimating Equations (GEE; Liang & Zeger, 1986). However, if the model includes time-varying covariates that depend on previous outcomes or previous interventions (e.g., prior self-monitoring behaviors or craving measured prior to decision point t ), these methods can result in inconsistent estimators (i.e., estimators that are different from the true parameter value even in large samples) for the proximal effects of A i , t (see Qian et al., 2022 ; Qian et al., 2020 ). In this case, the weighted and centered least-squares (WCLS) estimation procedure developed by Murphy and colleagues ( Boruvka et al., 2018 ) can be employed. Note that while WCLS provides consistent estimators of the proximal effects of A i , t (marginal or conditional on Z i 11 and Z i 12 ), it may not ameliorate the problem for other proximal effects (e.g., the proximal main effect of Z i 11 ). An accessible overview of this method is provided by Qian and colleagues (2022) .

Hybrid SMART-MRT

Suppose investigators are motivated to answer the following questions about the development of a weight loss intervention that offers a mobile app to participants at the beginning of the program. First (Q7), at the beginning of the program is it beneficial (in terms of weight loss at month 6) to augment the app with coaching (Add Coaching)? Next (Q8), at week 2, is it beneficial (in terms of weight loss at month 6) to add meal replacement (Add Meal) to individuals who show early signs of non-response? Finally (Q9), is it beneficial (in terms of increasing self-monitoring of dietary intake in the next 12 hours) to deliver a mobile-based prompt at mid-day (Prompt)? Note that Q7 and Q8 concern different components that can each be initiated at a single, unique decision point—at program entry (Add Coaching) and at week 2 (Add Meal), respectively. On the other hand, Q9 concerns a time-varying component, and the decision to deliver it or not can be made daily (Prompt). Also notice that, consistent with the timescale at which the component of interest can be delivered, Q7 and Q8 focus on a distal outcome (weight loss at month 6) whereas Q9 concerns a proximal outcome (self-monitoring of dietary intake in the next 12 hours).

To answer these questions, investigators may consider an experiment with three factors, one for each component. Here, Add Coaching refers to the factor corresponding to augmenting the app with coaching at program entry, Add Meal refers to the factor corresponding to adding meal replacement to non-responders at week 2, and Prompt refers to the factor corresponding to delivering a mid-day prompt to motivate self-monitoring. Each factor will have two levels: On and Off. Since decisions regarding the component Add Coaching should be made at the beginning of the program, study participants should be randomized to the corresponding factor Add Coaching at a single decision point (the beginning of the program). Further, since decisions regarding the component Add Meal should be made at week 2 and they only concern non-responders, the randomization to the corresponding factor Add Meal should take place at a single decision point (week 2) and involve only non-responders. Finally, since decisions about the delivery of the component Prompt can be made repeatedly, participants should be randomized to the corresponding factor Prompt at multiple decision points (i.e., daily at mid-day).

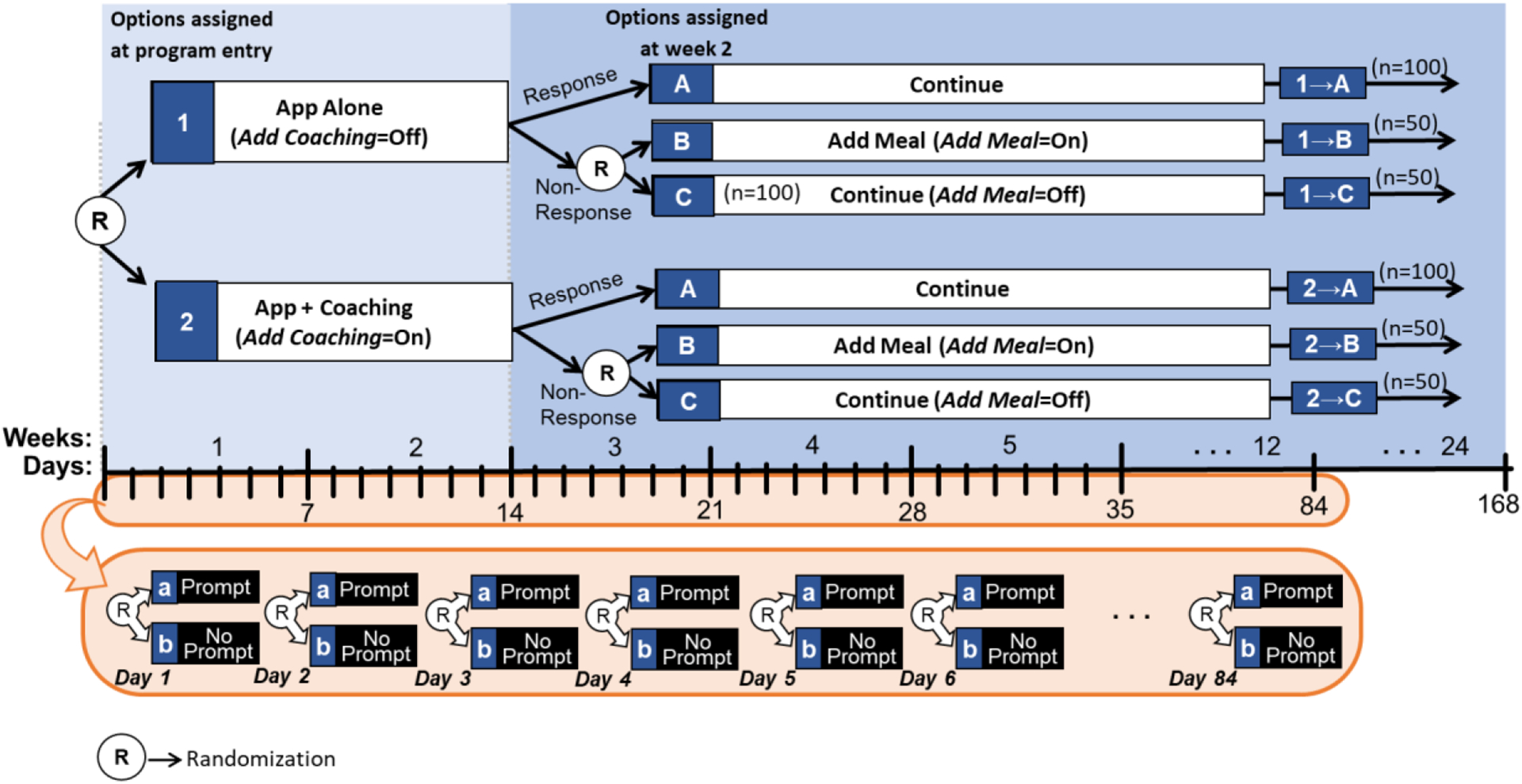
The experimental design in Figure 3a can provide data for addressing questions Q7–Q9. At program entry, participants are randomized to the two levels of the factor Add Coaching . Then, at week 2, non-responders are randomized to the two levels of the factor Add Meal , whereas responders continue with their assigned initial option. In addition, throughout the first 12 weeks, individuals are randomized daily, at midday, to the two levels of the factor Prompt . This design integrates a prototypical SMART with an MRT ( Nahum-Shani et al., 2022 ).

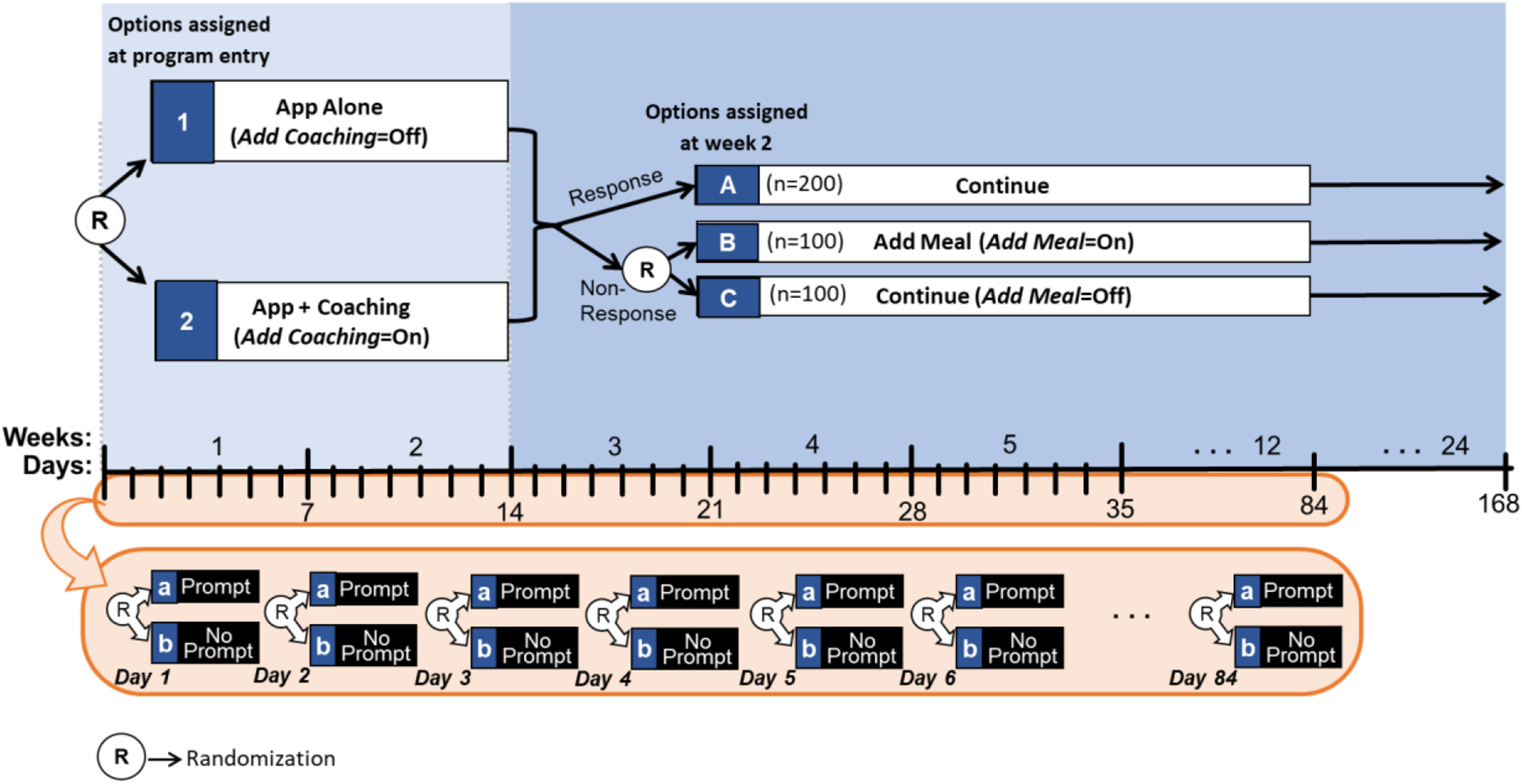
An Example Hybrid SMART-MRT

Suppose that 400 individuals enter the study and are randomized initially with equal probability (0.50) to the two levels of Add Coaching (i.e., n =200 participants in each option). Then, suppose that at week 2, 50% of the participants (i.e., n =200) are classified as responders ( n =200 in option A from Figure 3a ) and continue with the initial intervention. Those classified as non-responders ( n =200) are re-randomized with equal probability (0.50) to either Add Meal ( n =100 in option B from Figure 3a ) or continue with the initial intervention ( n =100 in option C from Figure 3a ). Then, suppose that every day, at mid-day, each individual is randomized with equal probability (0.5) to each of the two levels of Prompt , that is to either deliver a prompt ( n =100) or not ( n =100).

Note that the sequential randomization in Figure 3a leads to 6 experimental cells, which are detailed in Figure 3b . For example, participants who start with both App alone (option 1 at program entry) and then are classified as responders at week 2 and thus continue with the initial intervention (option A at week 2) are considered part of experimental cell 1→A. However, as before, the goal here is not to compare these cells but rather to combine multiple cells in different ways to answer the scientific questions outlined above ( Collins, 2018 ). Further, similar to a prototypical SMART design ( Nahum-Shani et al., 2020a ), there are four adaptive interventions that are embedded in this trial by design (see Table 5 ). However, it is important to note that in a hybrid SMART-MRT the adaptive interventions are embedded in the context of a pre-specified protocol for delivering a time-varying component (here the delivery of prompts with 0.5 probability each day) and thus their effects should be interpreted accordingly. Below, we discuss how data from this hybrid SMART-MRT design can be used to answer questions Q7–Q9.

Experimental Cells in the Example Hybrid SMART-MRT

Adaptive interventions embedded in the hybrid SMART-MRT in Figure 3

Data analytic approach for hybrid SMART-MRT.

A data analysis approach for the hybrid SMART-MRT would combine the special features of the hybrid factorial-SMART and hybrid factorial-MRT designs. Like the factorial-SMART design, the distinction between responders and non-responders is important, particularly when (as in our example) the re-randomization in the SMART is restricted to non-responders. Further, similar to the factorial-MRT design, the distinction between proximal and distal outcomes is also important. The notation, however, does not become much more complicated, and the underlying ideas are very similar.

Let Z i 1 be the randomized factor at program entry (here, Add Coaching ) and Z i 2 be the randomized factor at week 2 for non-responders (here, Add Meal ), each coded +1 for On and −1 for Off. As before, let X 0 denote mean-centered baseline covariates. Finally, let A i , t represent the time-varying factor (here, Prompt ) for individual i at time t , coded +1 for On (i.e., prompt) and −1 for Off (i.e., no prompt). As in the hybrid factorial-MRT, let Y i , t +Δ represent the proximal outcome (here, self-monitoring in the next 12 hours) and Y i * represent the distal outcome (here, month 6 weight loss). The following model can be estimated to answer questions about the distal main effects of the factor assigned at program entry and the factor assigned at week 2, as well as the interaction between them.

Model 4 is marginal over A ¯ i and it has essentially the same form as the marginal model for the distal outcome in a SMART without an MRT component (see Nahum-Shani et al., 2012a ). As in the case of a hybrid factorial-MRT, a more general model could instead be used to include an effect of A ¯ i , with a similar caveat that due to the law of large numbers, there will be little between-subject variability in A ¯ i (see Model 2 in Appendix A of Nahum-Shani et al., 2022 ).

Table 6 summarizes how the coefficients in Model (4) can be used to answer questions about the distal effects of the Z i 1 and Z i 2 . For example, the expected distal outcome for a participant who was offered coaching at program entry is E ( Y i * ∣ Z i 1 = + 1 ) = θ 1 , and the expected distal outcome for a participant who was not offered coaching at program entry is E ( Y i * ∣ Z i 1 = − 1 ) = − θ 1 . Therefore, the difference between these quantities, namely 2 θ 1 , can be used to answer question Q7, which concerns the main effect of the factor Add Coaching . Likewise, 2 θ 2 is the main effect of the factor Add Meal for non-responders, which is the focus of question Q8. Finally, as in Model 1 , linear combinations of the coefficients in Model 4 can be used to compare adaptive interventions that are embedded in the hybrid SMART-MRT, averaging over the time-varying factor. Specifically, the contrast between expected population outcomes under embedded adaptive interventions ( z 1 , z 2 ) and ( z 1 ′ , z 2 ′ ) is

Scientific questions about distal effects and model parameters for a hybrid SMART-MRT

Having considered the distal effects of the factors Z i 1 and Z i 2 , we now consider the proximal effects of the time-varying factor. The simplest model for answering question Q9, which concerns the effect of Prompt on self-monitoring in the next 12 hours, would be

where C i , t is a dummy (1/0) indicator of whether or not Z i 2 was assigned for individual i at time t . In the current example C i , t = 1{ t > K }, where K =14 days. This indicator is included to help ensure that the proximal effect of Prompt at each decision point is allowed to be impacted only by factors that were introduced prior to that decision point. In the current example, Z i 2 was assigned on day 14 and hence should be allowed to impact the proximal effect of the prompt only after day 14. Failure to respect this ordering may lead to bias and incorrect conclusions ( Dziak et al., 2019 ; Lu et al., 2016 ; Nahum-Shani et al., 2020b ). Equivalently, Z i 2 could be set to 0 by convention during the first stage, avoiding the need for the additional notation.

Similar to the hybrid factorial-MRT, a richer model could be specified to investigate whether the proximal effects are time-varying. For example, linearly time-varying effects could be explored using the model

where t is time since the randomization of Z i 1 , and t * is time since the randomization of Z i 2 . Quadratic or other nonlinear effects of time could also be explored. Table 7 summarizes how the coefficients in Model (5) can be used to answer a variety of scientific questions about the proximal main effect of the time-varying factor ( A i , t ) and its interactions with the factors assigned at the beginning of the program ( Z i 1 ) and at week 2 ( Z i 2 ). Note that the questions in Tables 6 and 7 are also discussed in Appendix A of Nahum-Shani et al. (2022) .

Scientific questions about proximal effects and model parameters for a hybrid SMART-MRT

Just as in the hybrid factorial-SMART, some estimands of interest for hybrid SMART-MRT designs require handling the fact that Z i 2 is not assigned to responders. The W&R approach described earlier in the context of the hybrid factorial-SMART, can also be applied for the hybrid SMART-MRT design (see Nahum-Shani et al., 2022 ). Recall that this approach involves replicating observations (rows in the dataset) of responders and assigning inverse probability weights to each observation. However, when modeling proximal effects, the hybrid SMART-MRT requires a slightly different approach to W&R than the hybrid factorial-SMART. This is because the repeated measures of Y i , t +Δ , one for each t = 1, … , T , are not independent within individual i , so that individual i is a cluster, even before replication. A non-responder would potentially be a cluster of size T (although some occasions may not be counted because of missing data). A responder would be a larger cluster due to the replication of their observations. For example, replicating all data from a responder would lead to a cluster of size 2 T , each row of which would be given half the weight of a data row from a non-responder. However, since Z i 2 was only assigned on week 2 (day 14) and hence should not have any effect on the proximal outcome before t = 14, it should be sufficient to replicate only the data from after the randomization to Z i 2 and simply treat Z i 2 as 0 otherwise.

Illustrative Data Analysis Based on the Weight Loss Hybrid SMART-MRT

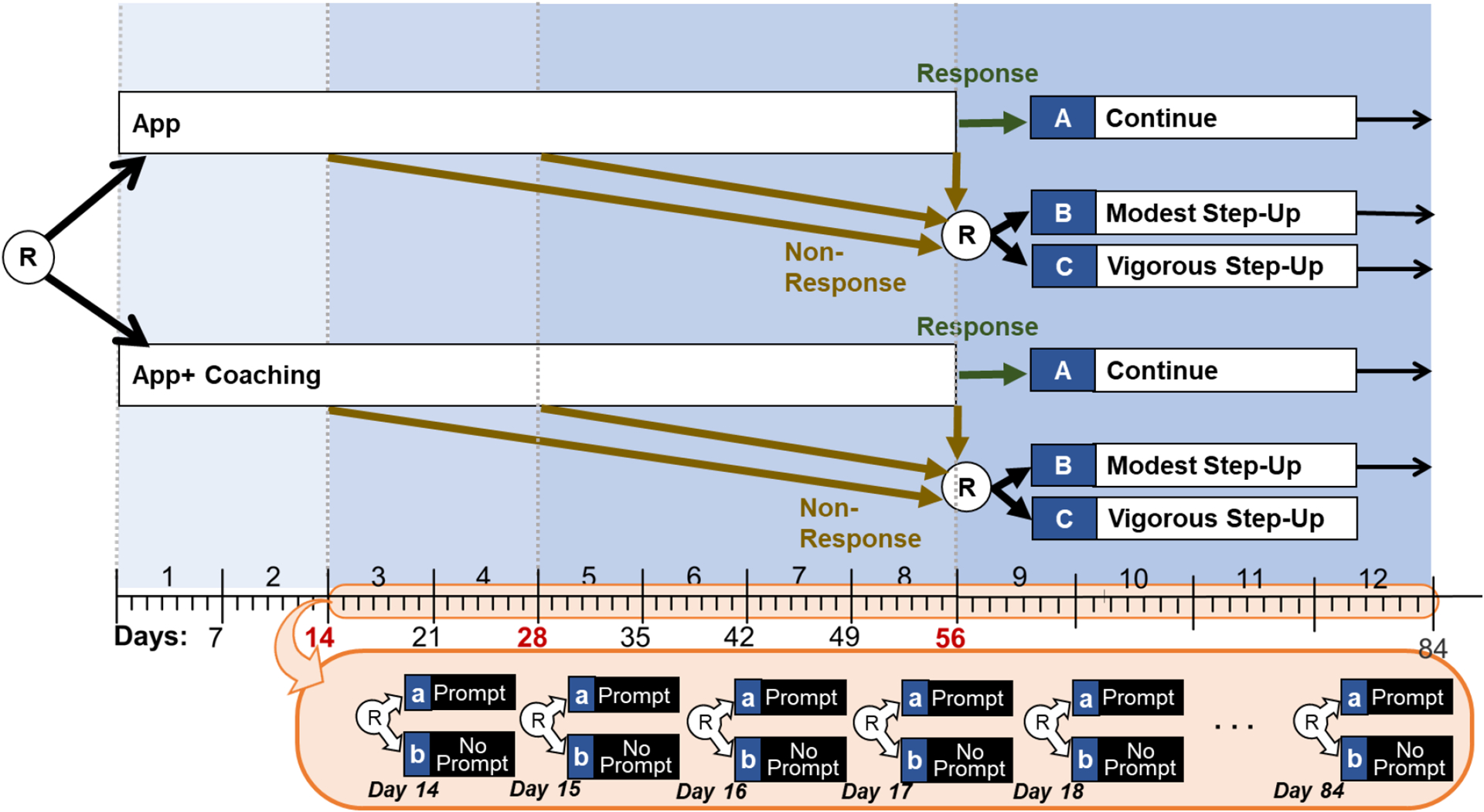
The SMART weight loss study ( Pfammatter et al., 2019 ) is a hybrid SMART-MRT. However, the design structure differs from the structure of the hybrid SMART-MRT in Figure 3 in two important ways (see Figure 4 ). First, the tailoring variable embedded in the SMART was time-varying, meaning that participants’ response status was assessed repeatedly, and they were re-randomized to second-stage options at the first time point in which they were classified as non-responders (unless and until that occurred, they continued with the initial intervention option). Second, micro-randomizations were employed only for non-responders and only following their classification as non-responders. Below we describe this study design in more detail and discuss how data from this study can be analyzed to answer scientific questions about possible synergies between components that can be delivered and adapted on different timescales. For illustrative purposes, we generated and analyzed simulated data that mimic key characteristics of real data from this study. These simulated data, as well as the data analysis code and related documentation are available at [ https://d3c.isr.umich.edu/software/main-and-moderated-effect-digital-components/ ]. Data were analyzed using R, version 4.2.0 (R Core Team, 2022).

The hybrid SMART-MRT weight loss study

Study Design

At the beginning of the study, participants were randomly assigned (with probability 0.5) to either a weight loss smartphone app alone (App) or to an app combined with weekly coaching (App + Coaching). At weeks 2, 4, and 8, participants’ early response status was assessed using average weekly weight loss. At the first time point at which a given participant had an average weekly weight loss of less than 0.5 pounds, they were classified as a non-responder and were randomly assigned (with probability 0.5) to either step-up modestly (by adding text messages) or vigorously (by adding text messages combined with another, more traditional weight loss treatment component that the participant was not offered initially; for details, see Pfammatter et al., 2019 ) for the remaining intervention period (i.e., until week 12). As long as the participant was classified as a responder, they continued with the initial intervention and were not re-randomized.

The text messages, which were included in both the modest and the vigorous step-up options for non-responders, involved micro-randomizations. Specifically, as soon as the participant was classified as a non-responder, they were randomly assigned daily (in the middle of the day), to either a text message (i.e., a prompt) that encouraged them to self-monitor their dietary intake (with 0.66 probability) or no message (i.e., no prompt).

The study enrolled 400 individuals between the ages of 18 and 60 with body mass index (BMI) between 27 and 45 kg/m 2 ( Spring et al., 2020 ). Given the illustrative nature of this analysis, we simulated data to mimic results from a subsample of 366 individuals (23.8% males; mean age 40.6 years) who did not drop out and who had complete data on all variables required for estimating both the proximal and distal effects discussed below. Of this subsample, 181 participants were randomly assigned to App alone ( Z i 1 = −1), and 185 were randomly assigned to App + Coaching ( Z i 1 = 1) at the beginning of the study. Then, over the twelve-week intervention period, 169 participants were classified as non-responders (96 at the second week, 45 at the fourth week, 28 at the eighth week). Eighty-four non-responders were randomly assigned to the modest step-up ( Z i 2 = −1) and 85 were assigned to the vigorous step-up ( Z i 2 = 1). 197 participants were classified as responders and continued with their assigned initial intervention.

Primary proximal outcome.

We consider dietary intake self-monitoring in the next 12 hours as the primary proximal outcome. This is a binary proximal outcome indicating whether (=1) or not (=0) the participant used the mobile app to record their dietary intake in the 12 hours following micro-randomization.

Primary distal outcome.

We consider weight loss from baseline to month 6 as the distal outcome. Body weight at baseline and month 6 was measured to the nearest 0.25 lb. using a calibrated balance beam scale (see Pfammatter et al., 2019 ).

Baseline measures.

Our models included two baseline measures as control covariates: (1) BMI calculated using the Quetelet index as weight in pounds / (height in inches) 2 × 704.5; and (2) biological sex.

This illustrative analysis was motivated by scientific questions concerning possible synergies between three components: (1) offering coaching initially; (2) stepping up vigorously for non-responders; and (3) prompting at mid-day. Specifically, the goal was to investigate (a) whether the proximal effect of prompting (vs. not prompting) on dietary intake self-monitoring in the next 12 hours varies by whether coaching was offered initially (vs. mobile app alone) and by whether a vigorous (vs. modest) step-up was offered to non-responders; and (b) whether the distal effect of offering coaching initially (vs. mobile app alone) on weight loss by month 6 varies by whether a vigorous (vs. modest) step-up was offered to non-responders and by the rate of prompts delivered to non-responders.

Given the unique features of this design, the models for the proximal and distal outcomes had to be modified in several ways. For the proximal outcome, the indicator C it for whether or not Z i 2 was assigned for individual i at time t , was included in all the coefficients involving either Z i 2 or A i , t (and not only Z i 2 as in Model 5 ), in the following way:

This modification was needed because the daily randomizations to prompt vs. no prompt ( A i , t ) took place only for non-responders and only after they were classified as non-responders. Further, since the tailoring variable (response status) was time-varying, we included the week in which the participant was classified as a non-responder (this variable was coded 0 for responders) as a control covariate in the model. We also included as a control covariate the number of days elapsed since the start of the subsequent intervention (for responders we considered the end of week 8 as the start of the subsequent intervention). Finally, since the proximal outcome is binary, we used a log-link function such that the effects are expressed on the “risk-ratio” scale. For example, the proximal main effect of delivering a prompt (averaging over the other components and all decision points) is expressed in terms of the probability of proximal self-monitoring when a prompt was delivered, divided by the probability of proximal self-monitoring when a prompt was not delivered (see Qian et al., 2020 ).

For the distal outcome model, we investigated the moderating role of the rate of prompts delivered ( A ¯ i ) by restricting the analysis to non-responders ( R = 0), since only non-responders were randomized daily to prompt delivery. Specifically, we used the following model:

The results described here are based on simulated data that mimic key characteristics of real data from the SMART weight loss study. Table 8 presents the results for the proximal outcome model. These results indicate that the main effect of delivering (vs. not delivering) a prompt on proximal self-monitoring of dietary intake, as well as the interactions between this time-varying factor, the initial intervention options, and the subsequent options for non-responders, are not significantly different from zero (i.e., all 95% confidence intervals [CIs] include zero).

Proximal model results

Proximal outcome: self-monitoring of dietary intake (yes/no) in the next 12 hours

SE: standard error; CI: confidence interval; LL: lower limit; UL: upper limit; BMI: body mass index

Although estimates pertaining to the control variables are provided for completeness, we caution readers against interpreting them since correct specification of this part of the model is not required to yield consistent estimates of the causal effect of the randomized messages (see Boruvka et al., 2017).

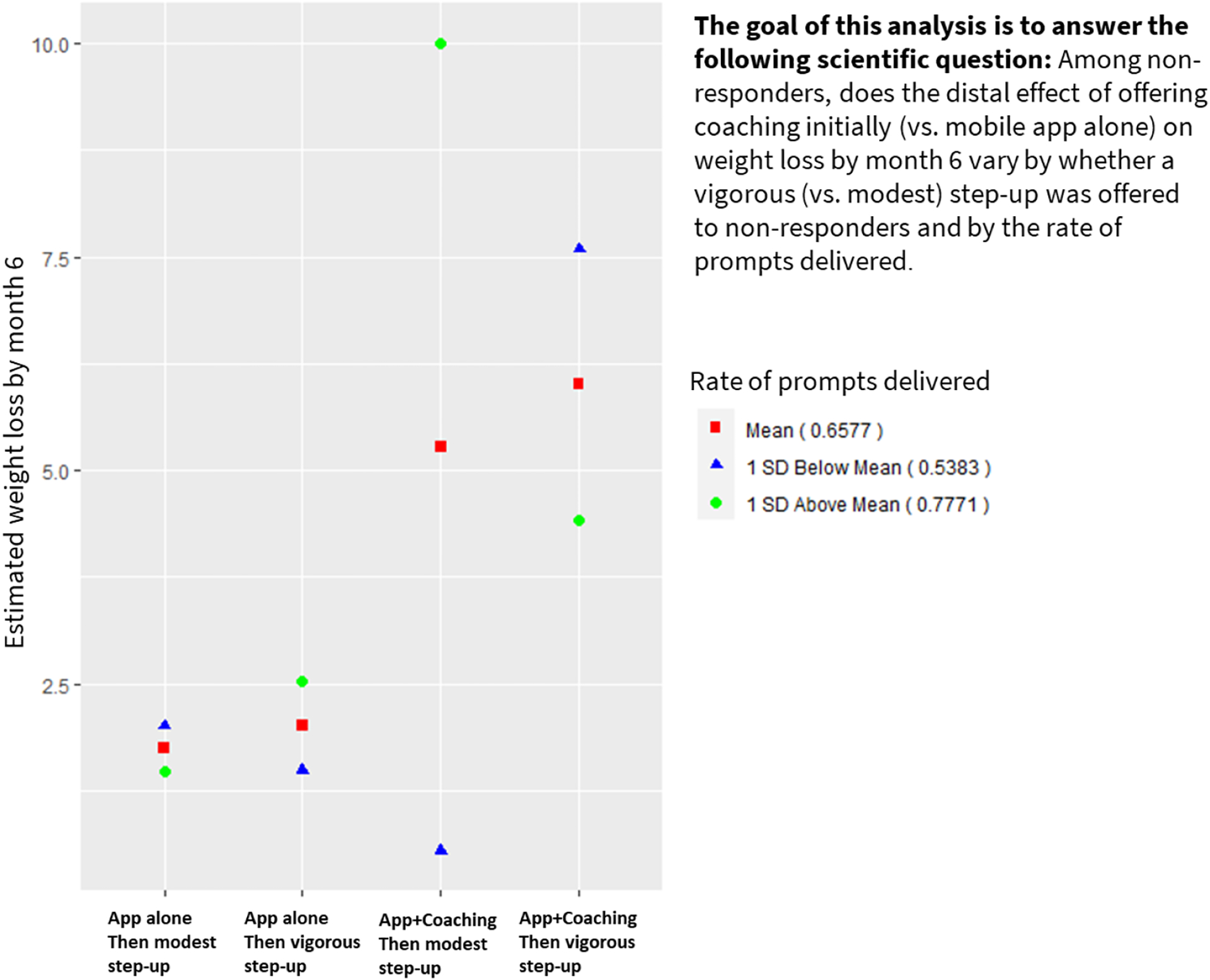
Table 9 presents the results for the distal outcome model among non-responders. These results show a significant three-way interaction between the initial options, step-up options, and the rate of prompts delivered among non-responders (Est =−14.85; 95% CI: [−24.39, −5.32]). Figure 5 summarizes the estimated weight loss by the initial options, step-up options, and the rate of prompts delivered. It shows that weight loss does not vary by the rate of prompts delivered for non-responders who started with App alone (regardless of their assigned step-up option). However, non-responders who started with App + Coaching and were then offered a modest step-up, lost more weight to the extent that more prompts were delivered. For non-responders who started with App + Coaching and were then offered a vigorous step-up, more weight was lost to the extent that fewer prompts were delivered. Overall, these results highlight the possibility that in the context of a mobile-based weight loss intervention that offers a relatively intense level of support (i.e., initial coaching and vigorous step up), high prompt delivery rate may be too burdensome and hence less effective.

Distal model results for non-responders, investigating the role of message rate

Distal outcome: weight loss by month 6

Results from simulated data the mimic the hybrid SMART-MRT weight loss study

In this paper we presented three types of HEDs. The first integrates a standard factorial design with a SMART design (i.e., hybrid factorial-SMART), the second integrates a standard factorial design with an MRT design (i.e., hybrid factorial-MRT), and the third integrates a SMART design with an MRT design (i.e., hybrid SMART-MRT). For each HED, we have proposed a model and a data analysis method that researchers can employ to answer questions about the selection and adaptation of intervention components on multiple timescales. These designs are especially promising given the increased interest in multimodality interventions that combine human-delivered interventions (e.g., therapy or coaching sessions delivered by a clinician or support group) with digital support (e.g., reminders or motivational messages delivered via a mobile app). Human-delivered and digital components can typically be delivered and adapted on very different timescales, usually slow (e.g., every few weeks or months) in the case of human-delivered components and fast (e.g., every few hours or minutes) in the case of digital components. The HED enables researchers to answer scientific questions about how best to integrate human-delivered and digital support by randomizing participants to human-delivered components and digital components simultaneously at their proper timescales.

This paper is intended not only to serve as a guide for the design and analysis of data from HEDs, but also to serve as a launching point for further research into methodological and practical issues related to these designs. There are multiple ways in which the ideas proposed here can be further developed by additional work. These include the development of sample size planning resources, missing data considerations, extensions to various types of outcomes, and extensions to accommodate variations within each type of HED. Below, we elaborate on each research direction.

Sample size planning for HEDs is an important topic for future research. Power planning resources do exist for standard factorial designs, SMARTs and MRTs. Therefore, a straightforward approach might be to use existing sample size resources for one of the designs comprising the HED; the selected design should likely be the one that is most relevant to the primary scientific question motivating the HED. For example, consider the hybrid SMART-MRT in Figure 3 . If the primary research question concerns the main effect of the component delivered at program entry (i.e., Add Coaching) in terms of month 6 weight loss (averaging over the other components and all decision points), then investigators may consider planning sample size using existing power resources for SMARTs ( Oetting et al., 2007 ). In this case, power would probably be lower, all else being equal, for the main effect of the component delivered at week 2 (Add Meal) on weight loss at month 6 because not all participants would be randomized on that corresponding factor. Power might be higher for testing the main effect of the time-varying factor Prompt on the proximal outcome because this comparison leverages both between-person and within-person contrasts. Alternatively, if the primary question concerns the main effect of the time-varying component Prompt on proximal self-monitoring behaviors (averaging over the other components and all decision points), then investigators may consider planning sample size using existing power resources for MRTs ( Liao et al., 2016 ). In this case, power would probably be lower for testing the main effects of the components at program entry and at week 2. While straightforward, this approach cannot be used to plan sample size for answering scientific questions about some of the interactions between components (e.g., the interaction between Add Coaching and Prompt in terms of the proximal outcome). If sample size for these questions is of interest, it could be investigated with simulations (e.g., see appendix B in Nahum-Shani et al., 2022 ). Given appropriate simplifying assumptions, sample size formulas might be derived in some cases.

Although HEDs are motivated by multiple scientific questions concerning the delivery and adaptation of several intervention components, similar to standard factorial designs (see Collins, 2018 ), we do not recommend controlling for multiple testing of these components. Controlling for multiple testing means that each hypothesis is tested with a Type I error rate that is substantially smaller than the traditional α = .05 and thus lower power for detecting effects. Because the aim of the analysis is to inform the construction of an intervention (that will later be compared to a suitable control using the traditional α = .05; see Collins et al., 2009 ), from a practical standpoint it is sensible to tolerate a greater probability of detecting a false effect in order to improve the ability to detect true effects ( Collins et al., 2009 ; Dziak et al., 2012 ; Nahum-Shani et al., 2017 ).

For simplicity of presentation, we did not consider missing data issues in this paper. The simplest way to account for expected missing data when planning a study would be to inflate the planned sample size to compensate (e.g., multiply the planned n by 1/(1 − m ) if a proportion m or less of missingness is expected). When analyzing the data, no guidelines specific to HEDs yet exist. Multiple imputation is probably preferable to listwise deletion, as in other settings, but more work remains to be done on how to best use features of the HED to inform the imputation model. It may also be interesting to study attrition in its own right, perhaps in addition to accounting for it in other analyses. For example, daily prompts might either increase or decrease the likelihood of dropout. Investigators could plan the primary analysis on an intent-to-treat basis and supplement it with an exploratory analysis in which dropout itself is also treated as a binary outcome.

The simple models presented early in this paper were all linear models with an identity link function. This might be inappropriate for some outcome variables, especially binary or categorical outcomes, which could be modeled using a log or logistic link function, as in the empirical data presented in the second part of the paper. Binary or other categorical outcomes would still have implications for power, and perhaps for the specific interpretation of some comparisons, because these link functions generally assume a non-additive model having non-orthogonal effects. For example, floor and ceiling effects or even complete separation can sometimes occur when fitting complicated models to binary data. More work is needed to understand the implications of employing the proposed data analytic methods with different types of outcomes.

In addition to the practical issues described above, the designs presented here can be extended in additional ways. For example, in HEDs that involve the MRT, instead of micro-randomizing participants to the time-varying factor with the same probability at each decision point, randomization probabilities may vary systematically between participants (e.g., in a hybrid factorial-MRT, participants may be randomized at program entry to either be prompted with 0.4 probability on each day or with 0.6 probability on each day). There are many other possible variations depending on the structure of the intervention to be developed and the scientific questions motivating the study. Guidelines are needed for whether and how the proposed data analytic methods should be modified to accommodate design variations.

The types of HEDs discussed here are all extensions of factorial designs. They share some of the benefits of factorial designs, such as the ability to explore interactions and the efficiency gained from investigating multiple factors in a single sample. They may also share the challenges of factorial designs, such as the need for appropriate model assumptions, the task of prioritizing the most important questions out of the many which can be answered, and the importance of planning for feasibility and fidelity of treatment delivery in multiple different conditions. Further work will help address these challenges as HEDs become more prevalent in behavioral and health sciences.

Acknowledgments

This work was funded by National Institutes of Health, Grants U01 CA229437, P50 DA054039, R01 DA039901, and R01 DK108678

Contributor Information

Inbal Nahum-Shani, Institute for Social Research, University of Michigan.

John J. Dziak, Institute for Health Research and Policy, University of Illinois Chicago

Hanna Venera, School of Public Health and Institute for Social Research, University of Michigan.

Angela F Pfammatter, College of Education, Health, and Human Sciences, The University of Tennessee Knoxville.

Bonnie Spring, Feinberg School of Medicine, Northwestern University.

Walter Dempsey, School of Public Health and Institute for Social Research, University of Michigan.

• Bernacer J, & Murillo JI (2014). The Aristotelian conception of habit and its contribution to human neuroscience. Frontiers in Human Neuroscience, 8(November), 883–883. 10.3389/fnhum.2014.00883 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Boruvka A, Almirall D, Witkiewitz K, & Murphy SA (2018). Assessing Time-Varying Causal Effect Moderation in Mobile Health. Journal of the American Statistical Association, 113(523), 1112–1121. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Brumback BA (2009). A note on using the estimated versus the known propensity score to estimate the average treatment effect. Statistics & Probability Letters, 79(4), 537–542. [ Google Scholar ]
• Chakraborty B, Collins LM, Strecher VJ, & Murphy SA (2009). Developing multicomponent interventions using fractional factorial designs. Statistics in Medicine, 28(21), 2687–2708. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Collins LM (2018). Optimization of behavioral, biobehavioral, and biomedical interventions: The multiphase optimization strategy (MOST). Springer. [ Google Scholar ]
• Collins LM, Dziak JJ, & Li R (2009). Design of experiments with multiple independent variables: A resource management perspective on complete and reduced factorial designs. Psychological Methods, 14(3), 202–224. 10.1037/a0015826 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Collins LM, Murphy SA, Nair VN, & Strecher VJ (2005). A strategy for optimizing and evaluating behavioral interventions. Annals of Behavioral Medicine, 30(1), 65–73. [ DOI ] [ PubMed ] [ Google Scholar ]
• Dziak JJ, Nahum-Shani I, & Collins LM (2012). Multilevel factorial experiments for developing behavioral interventions: power, sample size, and resource considerations. Psychological Methods, 17(2), 153. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Dziak JJ, Yap JR, Almirall D, McKay JR, Lynch KG, & Nahum-Shani I (2019). A data analysis method for using longitudinal binary outcome data from a SMART to compare adaptive interventions. Multivariate behavioral research, 54(5), 613–636. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Fernandez ME, Schlechter CR, Del Fiol G, Gibson B, Kawamoto K, Siaperas T, Pruhs A, Greene T, Nahum-Shani I, & Schulthies S (2020). QuitSMART Utah: an implementation study protocol for a cluster-randomized, multi-level Sequential Multiple Assignment Randomized Trial to increase Reach and Impact of tobacco cessation treatment in Community Health Centers. Implementation Science, 15(1), 1–13. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Ghosh P, Nahum-Shani I, Spring B, & Chakraborty B (2020). Noninferiority and equivalence tests in sequential, multiple assignment, randomized trials (SMARTs). Psychological Methods, 25(2), 182. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hernan MA, Brumback BA, & Robins JM (2002). Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Stat Med, 21(12), 1689–1709. [ DOI ] [ PubMed ] [ Google Scholar ]
• Hirano K, Imbens GW, & Ridder G (2003). Efficient estimation of average treatment effects using the estimated propensity score. Econometrica, 71(4), 1161–1189. [ Google Scholar ]
• Koch ED, Moukhtarian TR, Skirrow C, Bozhilova N, Asherson P, & Ebner-Priemer UW (2021). Using e-diaries to investigate ADHD–State-of-the-art and the promising feature of just-in-time-adaptive interventions. Neuroscience & Biobehavioral Reviews, 127, 884–898. [ DOI ] [ PubMed ] [ Google Scholar ]
• Lavori PW, & Dawson R (2000). A design for testing clinical strategies: biased adaptive within-subject randomization. Journal of the Royal Statistical Society: Series A (Statistics in Society), 163(1), 29–38. [ Google Scholar ]
• Liao P, Klasnja P, Tewari A, & Murphy SA (2016). Sample size calculations for micro-randomized trials in mHealth. Statistics in Medicine, 35(12), 1944–1971. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Lu X, Nahum-Shani I, Kasari C, Lynch KG, Oslin DW, Pelham WE, Fabiano G, & Almirall D (2016). Comparing dynamic treatment regimes using repeated-measures outcomes: modeling considerations in SMART studies. Statistics in Medicine, 35(10), 1595–1615. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Mohr D, Cuijpers P, & Lehman K (2011). Supportive accountability: a model for providing human support to enhance adherence to eHealth interventions. Journal of Medical Internet Research, 13(1), e30. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Murphy SA (2005). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine, 24(10), 1455–1481. [ DOI ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, & Almirall D (2019). An Introduction to Adaptive Interventions and SMART Designs in Education. NCSER 2020–001. National center for special education research. [ Google Scholar ]
• Nahum-Shani I, Almirall D, Yap JR, McKay JR, Lynch KG, Freiheit EA, & Dziak JJ (2020a). SMART longitudinal analysis: A tutorial for using repeated outcome measures from SMART studies to compare adaptive interventions. Psychological Methods, 25(1), 1–29. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Almirall D, Yap JRT, McKay JR, Lynch KG, Freiheit EA, & Dziak JJ (2020b). SMART longitudinal analysis: A tutorial for using repeated outcome measures from SMART studies to compare adaptive interventions. Psychological Methods, 25(1), 1–29. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, & Dziak JJ (2018). Multilevel Factorial Designs in Intervention Development. In Collins LM & Kugler KC (Eds.), Optimization of Behavioral, Biobehavioral, and Biomedical Interventions: Advanced Topics (pp. 47–87). Springer International Publishing. 10.1007/978-3-319-91776-4_3 [ DOI ] [ Google Scholar ]
• Nahum-Shani I, Dziak JJ, & Collins LM (2018). Multilevel factorial designs with experiment-induced clustering. Psychological Methods, 23(3), 458–479. 10.1037/met0000128 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Dziak JJ, Walton MA, & Dempsey W (2022). Hybrid Experimental Designs for Intervention Development: What, Why and How. Advances in Methods and Practices in Psychological Science, 5(3). 10.1177/25152459221114279 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Dziak JJ, & Wetter DW (2022). MCMTC: A Pragmatic Framework for Selecting an Experimental Design to Inform the Development of Digital Interventions. Frontiers in Digital Health, 4. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Hekler E, & Spruijt-Metz D (2015). Building health behavior models to guide the development of just-in-time adaptive interventions: a pragmatic framework. Health Psychology, 34(Supp), 1209–1219. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano GA, Waxmonsky JG, Yu J, & Murphy SA (2012a). Experimental design and primary data analysis methods for comparing adaptive interventions. Psychological Methods, 17(4), 457–477. 10.1037/a0029372 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano GA, Waxmonsky JG, Yu J, & Murphy SA (2012b). Q-learning: a data analysis method for constructing adaptive interventions. Psychological Methods, 17(4), 478–494. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Shaw SD, Carpenter SM, Murphy SA, & Yoon C (2022). Engagement in digital interventions. American Psychologist. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nahum-Shani I, Ertefaie A, Lu X, Lynch KG, McKay JR, Oslin DW, & Almirall D (2017). A SMART data analysis method for constructing adaptive treatment strategies for substance use disorders. Addiction, 112(5), 901–909. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Nair V, Strecher V, Fagerlin A, Ubel P, Resnicow K, Murphy S, Little R, Chakraborty B, & Zhang A (2008). Screening experiments and the use of fractional factorial designs in behavioral intervention research. American Journal of Public Health, 98(8), 1354–1359. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Oetting AI, Levy JA, Weiss RD, & Murphy SA (2007). Statistical methodology for a SMART design in the development of adaptive treatment strategies. In Shrout P, Keyes K, & Ornstein K (Eds.), Causality and Psychopathology : Finding the Determinants of Disorders and Their Cures (pp. 179–205). Oxford University Press. [ Google Scholar ]
• Orellana L, Rotnitzky A, & Robins JM (2010). Dynamic regime marginal structural mean models for estimation of optimal dynamic treatment regimes, Part I: main content. Int J Biostat, 6(2), Article 8. https://www.ncbi.nlm.nih.gov/pubmed/21969994 [ PubMed ] [ Google Scholar ]
• Pfammatter AF, Nahum-Shani I, DeZelar M, Scanlan L, McFadden HG, Siddique J, Hedeker D, & Spring B (2019). SMART: Study protocol for a sequential multiple assignment randomized controlled trial to optimize weight loss management. Contemporary clinical trials, 82, 36–45. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Qian T, Walton AE, Collins LM, Klasnja P, Lanza ST, Nahum-Shani I, Rabbi M, Russell MA, Walton MA, & Yoo H (2022). The microrandomized trial for developing digital interventions: Experimental design and data analysis considerations. Psychological Methods. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Qian T, Yoo H, Klasnja P, Almirall D, & Murphy SA (2020). Estimating time-varying causal excursion effects in mobile health with binary outcomes. Biometrika. 10.1093/biomet/asaa070 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Ritterband LM, Thorndike FP, Cox DJ, Kovatchev BP, & Gonder-Frederick LA (2009). A behavior change model for internet interventions. Annals of Behavioral Medicine, 38(1), 18–27. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Robins J, Orellana L, & Rotnitzky A (2008). Estimation and extrapolation of optimal treatment and testing strategies. Statistics in Medicine, 27(23), 4678–4721. 10.1002/sim.3301 [ DOI ] [ PubMed ] [ Google Scholar ]
• Schueller SM, Tomasino KN, & Mohr DC (2017). Integrating human support into behavioral intervention technologies: the efficiency model of support. Clinical Psychology: Science and Practice, 24(1), 27–45. [ Google Scholar ]
• Spring B, Pfammatter A, Scanlan L, H.G. M, Marchese S, Siddique J, Hedeker D, & Nahum-Shani I (2020). How Low Can We Go? Optimal First Line and Augmentation Treatment Tactics for Obesity Stepped Care. Obesity, 28(S2):(106), 216. [ Google Scholar ]
• Stanger C, Kowatsch T, Xie H, Nahum-Shani I, Lim-Liberty F, Anderson M, Santhanam P, Kaden S, & Rosenberg B (2021). A digital health intervention (SweetGoals) for young adults with type 1 diabetes: protocol for a factorial randomized trial. JMIR Research Protocols, 10(2), e27109. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Walton A, Nahum-Shani I, Crosby L, Klasnja P, & Murphy S (2018). Optimizing Digital Integrated Care via Micro-Randomized Trials. Clinical Pharmacology & Therapeutics, 104(1), 53–58. https://doi.org/ 10.1002/cpt.1079 [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Webb CA, & Cohen ZD (2021). Progress towards clinically informative data-driven decision support tools in psychotherapy. The Lancet Digital Health, 3(4), e207–e208. [ DOI ] [ PubMed ] [ Google Scholar ]
• Wentzel J, van der Vaart R, Bohlmeijer ET, & van Gemert-Pijnen JE (2016). Mixing online and face-to-face therapy: How to benefit from blended care in mental health care. JMIR Mental Health, 3(1), e9. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (1.9 MB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Popular searches

• How to Get Participants For Your Study
• How to Do Segmentation?
• Conjoint Preference Share Simulator
• MaxDiff Analysis
• Likert Scales
• Reliability & Validity

Request consultation

Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.

Looking for an online survey platform?

Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.

Research Methods Knowledge Base

• Navigating the Knowledge Base
• Foundations
• Measurement
• Internal Validity
• Introduction to Design
• Types of Designs
• Two-Group Experimental Designs
• Defining Experimental Designs
• Factorial Designs
• Randomized Block Designs
• Covariance Designs

Hybrid Experimental Designs

• Quasi-Experimental Design
• Pre-Post Design Relationships
• Designing Designs for Research
• Quasi-Experimentation Advances
• Table of Contents

Hybrid experimental designs are just what the name implies ⁠— new strains that are formed by combining features of more established designs. There are lots of variations that could be constructed from standard design features. Here, I’m going to introduce two hybrid designs. I’m featuring these because they illustrate especially well how a design can be constructed to address specific threats to internal validity.

The Solomon Four-Group Design

The Solomon Four-Group Design is designed to deal with a potential testing threat . Recall that a testing threat occurs when the act of taking a test affects how people score on a retest or posttest. The design notation is shown in the figure. It’s probably not a big surprise that this design has four groups. Note that two of the groups receive the treatment and two do not. Further, two of the groups receive a pretest and two do not. One way to view this is as a 2x2 (Treatment Group X Measurement Group) factorial design . Within each treatment condition we have a group that is pretested and one that is not. By explicitly including testing as a factor in the design, we are able to assess experimentally whether a testing threat is operating.

Possible Outcomes. Let’s look at a couple of possible outcomes from this design. The first outcome graph shows what the data might look like if there is a treatment or program effect and there is no testing threat. You need to be careful in interpreting this graph to note that there are six dots – one to represent the average for each O in the design notation. To help you visually see the connection between the pretest and posttest average for the same group, a line is used to connect the dots. The two dots that are not connected by a line represent the two post-only groups. Look first at the two pretest means. They are close to each because the groups were randomly assigned. On the posttest, both treatment groups outscored both controls. Now, look at the posttest values. There appears to be no difference between the treatment groups, even though one got a pretest and the other did not. Similarly, the two control groups scored about the same on the posttest. Thus, the pretest did not appear to affect the outcome. But both treatment groups clearly outscored both controls. There is a main effect for the treatment.

Now, look at a result where there is evidence of a testing threat. In this outcome, the pretests are again equivalent (because the groups were randomly assigned). Each treatment group outscored it’s comparable control group. The pre-post treatment outscored the pre-post control. And, the post-only treatment outscored the post-only control. These results indicate that there is a treatment effect. But here, both groups that had the pretest outscored their comparable non-pretest group. That’s evidence for a testing threat.

Switching Replications Design

The Switching Replications design is one of the strongest of the experimental designs. And, when the circumstances are right for this design, it addresses one of the major problems in experimental designs ⁠— the need to deny the program to some participants through random assignment. The design notation indicates that this is a two group design with three waves of measurement. You might think of this as two pre-post treatment-control designs grafted together. That is, the implementation of the treatment is repeated or replicated . And in the repetition of the treatment, the two groups switch roles – the original control group becomes the treatment group in phase 2 while the original treatment acts as the control. By the end of the study all participants have received the treatment.

The switching replications design is most feasible in organizational contexts where programs are repeated at regular intervals. For instance, it works especially well in schools that are on a semester system. All students are pretested at the beginning of the school year. During the first semester, Group 1 receives the treatment and during the second semester Group 2 gets it. The design also enhances organizational efficiency in resource allocation. Schools only need to allocate enough resources to give the program to half of the students at a time.

Possible Outcomes. Let’s look at two possible outcomes. In the first example, we see that when the program is given to the first group, the recipients do better than the controls. In the second phase, when the program is given to the original controls, they “catch up” to the original program group. Thus, we have a converge, diverge, reconverge outcome pattern. We might expect a result like this when the program covers specific content that the students master in the short term and where we don’t expect that they will continue getting better as a result.

Now, look at the other example result. During the first phase we see the same result as before ⁠— the program group improves while the control does not. And, as before, during the second phase we see the original control group, now the program group, improve as much as did the first program group. But now, during phase two, the original program group continues to increase even though the program is no longer being given them. Why would this happen? It could happen in circumstances where the program has continuing and longer term effects. For instance, if the program focused on learning skills, students might continue to improve even after the formal program period because they continue to apply the skills and improve in them.

I said at the outset that both the Solomon Four-Group and the Switching Replications designs addressed specific threats to internal validity. It’s obvious that the Solomon design addressed a testing threat. But what does the switching replications design address? Remember that in randomized experiments, especially when the groups are aware of each other, there is the potential for social threats ⁠— compensatory rivalry, compensatory equalization and resentful demoralization are all likely to be present in educational contexts where programs are given to some students and not to others. The switching replications design helps mitigate these threats because it assures that everyone will eventually get the program. And, it allocates who gets the program first in the fairest possible manner, through the lottery of random assignment.

Cookie Consent

Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.

For more information on Conjointly's use of cookies, please read our Cookie Policy .

Which one are you?

I am new to conjointly, i am already using conjointly.

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

• Publications
• Account settings
• Advanced Search
• Journal List

Effectiveness-implementation Hybrid Designs

Combining Elements of Clinical Effectiveness and Implementation Research to Enhance Public Health Impact

Geoffrey M Curran , PhD

Mark bauer , md, brian mittman , phd, jeffrey m pyne , md, cheryl stetler , phd.

• Author information
• Copyright and License information

Reprints: Geoffrey M. Curran, PhD, Department of Psychiatry, Division of Health Services Research, University of Arkansas for Medical Sciences, 4301 W. Markham St. #755, Little Rock, AR 72205. [email protected]

This study proposes methods for blending design components of clinical effectiveness and implementation research. Such blending can provide benefits over pursuing these lines of research independently; for example, more rapid translational gains, more effective implementation strategies, and more useful information for decision makers. This study proposes a “hybrid effectiveness-implementation” typology, describes a rationale for their use, outlines the design decisions that must be faced, and provides several real-world examples.

An effectiveness-implementation hybrid design is one that takes a dual focus a priori in assessing clinical effectiveness and implementation. We propose 3 hybrid types: (1) testing effects of a clinical intervention on relevant outcomes while observing and gathering information on implementation; (2) dual testing of clinical and implementation interventions/strategies; and (3) testing of an implementation strategy while observing and gathering information on the clinical intervention’s impact on relevant outcomes.

Conclusions

The hybrid typology proposed herein must be considered a construct still in evolution. Although traditional clinical effectiveness and implementation trials are likely to remain the most common approach to moving a clinical intervention through from efficacy research to public health impact, judicious use of the proposed hybrid designs could speed the translation of research findings into routine practice.

Keywords: diffusion of innovation, implementation science, clinical trials, pragmatic designs

Much has been written about the nature of health care science-to-service gaps both in general 1 – 3 and relative specifically to health promotion 4 and numerous medical specialties. 5 – 9 Thus far, the literature indicates that gaps between research and practice can result from multiple factors, including educational/knowledge deficiencies and/or disagreements, 10 , 11 time constraints for practitioners, 12 , 13 lack of decision support tools and feedback mechanisms, 13 poorly aligned incentives, 14 and a host of other organizational climate and cultural factors. 2 , 15 , 16

In addition to these provider-level and systems-level barriers to rapid translation, Glasgow et al 4 and others 17 – 20 argue that the time lag between research discovery and routine uptake is also inflated by the dominant developmental approach; that is, one that encourages delimited, step-wise progressions of research through clinical efficacy research, then clinical effectiveness research, and finally implementation research. In addition, it has been suggested that current conceptions of research designs fail to “maximize clinical utility for practicing clinicians and other decision makers” 18 ; for example, through a failure to focus on external validity or implementation-related barriers and facilitators to routine use and sustainability of “effective” practices. 4 , 21 , 22

Wells 19 and Glasgow et al 4 suggested that a blending of the efficacy and effectiveness stages of intervention development could improve the speed of knowledge creation and increase the usefulness and policy relevance of clinical research. We propose that a blending of the design components of clinical effectiveness trials and implementation trials also is feasible and desirable. Such blending can provide benefits over pursuing these lines of research independently; for example, more rapid translational gains in clinical intervention uptake, more effective implementation strategies, and more useful information for researchers and decision makers. This study describes the elements of such “effectiveness-implementation hybrid designs,” discusses the indications for such approaches, outlines the design decisions that must be faced in developing such protocols, and provides several examples of funded hybrid studies to illustrate the concepts.

DEFINING TERMINOLOGY

Terminology in this study has been informed by a glossary provided by the Department of Veterans Affairs Quality Enhancement Research Initiative (VA QUERI) 22 ; with which the authors are affiliated. VA QUERI is funded by the VA’s Health Services Research and Development Service and, through multiple centers across the nation, promotes and supports quality improvement and implementation research. 23 Key terms based on this nomenclature are defined in Table 1 . In addition, we propose the following definition: an effectiveness-implementation hybrid design is one that takes a dual focus a priori in assessing clinical effectiveness and implementation. Hybrid designs will typically take one of 3 approaches: (a) testing effects of a clinical intervention on relevant outcomes while observing and gathering information on implementation; (b) dual testing of clinical and implementation interventions/strategies; or (c) testing of an implementation strategy while observing and gathering information on the clinical intervention’s impact on relevant outcomes.

Key Terms and Definitions *

Many definitions based on the Quality Enhancement Research Initiative Glossary. 22

CHALLENGES IN LINKING CLINICAL AND IMPLEMENTATION RESEARCH DESIGNS

Clinical and implementation research, in their “ideal types,” typically do not share many design features. As depicted in Table 2 , key differences exist in terms of unit of analysis (perhaps the most obvious distinction), typical unit of randomization, outcome measures, and the targets of the interventions being tested. More specifically, highly controlled clinical efficacy research is most concerned with internal validity, that is, reducing threats to causal inference of the treatment under study, and evaluating symptom/functional-focused outcomes. 19 With more heterogeneous samples and study locations, and more attention given to a range of clinical and other outcomes (eg, quality of life, costs), clinical effectiveness research is more concerned with external validity or generalizability. 24 , 19 The most recent adaptation of these principles, to enhance the relevance of effectiveness designs for translation, are “practical clinical trials,” 17 , 18 which have found their newest application in the area of policy-relevant “comparative effectiveness research.” 25 In each of these clinical trial approaches, designs rely on controlling/ensuring delivery of the clinical intervention, albeit in a less restrictive setting, with little attention to implementation processes likely to be of relevance to transitioning the intervention to general practice settings.

Design Characteristics of Clinical Effectiveness and Implementation Trials (Ideal Types)

In contrast, implementation research is focused on the adoption or uptake of clinical interventions by providers and/or systems of care 2 , 22 , 26 ; and research outcomes are usually provider and/or system behaviors, for example, levels and rates of adoption and fidelity to the clinical intervention. Because implementation research often assumes a linear, step-wise approach to knowledge translation, clinical intervention effectiveness is often assumed, and he assessment of patient-level symptom/functional outcomes, therefore, is often not included in the designs.

Given the differing priorities, methods, and even language of effectiveness and implementation research ( Table 2 ), it is not surprising that few studies in the peer-reviewed literature are structured to address a priori both clinical intervention and implementation aims. Moreover, those published studies actually doing so have seldom explicitly recognized the hybrid nature of their designs or acknowledged/described the trade-offs entailed in such designs. This is understandable as there has been a dearth of explicit guidance on how such hybridization can be systematically attempted ( Fig. 1 ).

Research pipeline.

HYBRID DESIGNS: CONCEPTUAL DEVELOPMENT

The origins of the hybrid designs proposed herein result from our collective experience over many years in writing, reviewing, and conducting research projects across the efficacy–effectiveness-implementation spectrum. Under the umbrella of the VA QUERI and its implementation frameworks, 22 we formed a work group to explore the hybrid concept. The work group, consisting of the authors of the manuscript, brought expertise in implementation research, clinical effectiveness trials, cost effectiveness research, qualitative research, formative evaluation, evidence-based practice, and clinical expertise in psychiatry. The work group discussed the following issues: design elements, challenges, and potential areas or opportunities for blending effectiveness with implementation research designs to hasten the movement of interventions from effectiveness testing through implementation to public health impact. We initially articulated a definition of hybrid designs and tested it both logically and against existing studies. We then revised our definition and typology in light of this testing. We subsequently had the opportunity to make formal presentations to audiences of health services and implementation researchers and trainees, and incorporated their feedback.

The remainder of this study builds on our refined definition of hybrid design and its 3 types as articulated below, with the text amplifying and unpacking the information presented in 2 supporting tables. Table 3 provides a summary of hybrid research aims, design considerations, and trade-offs to be considered within each hybrid type. Table 4 provides funded and published or presented examples of type 1, 2, and 3 hybrid designs, along with a comparison with a published clinical effectiveness randomized-controlled trial and a nonhybrid implementation trial. Most of the examples of the proposed hybrids discussed in the text (except for 2) and all presented in Table 4 are from the VA. As noted above, we have approached this work based on our experience in a VA implementation research program, and most of the examples we know best come from the VA setting. In theory, the hybrid designs should not be more or less effective in the VA or any other setting (as was true for our 2 non-VA examples), and the recommended conditions we propose for their use are not exclusive to, or even more ideal in, a VA or other large/single-payer system.

Hybrid Design Characteristics and Key Challenges

In a grant application, one of these aims/research questions might take precedence, for example in a case where the test of an implementation intervention/strategy is exploratory. Yet, for the purposes of this table, we listed these dual aims/research questions as “coprimary.”

IRB indicates Institutional Review Board.

Hybrid Examples

Could be either a clinical intervention-related outcome or an implementation outcome depending on the a priori focus of the study.

CCM indicates chronic care model; FE, formative evaluation; OTM, Organizational Transformation Model; VA, Veterans Affairs; VISN, Veterans Integrated Services Network; VHA, Veterans Health Administration.

Hybrid Type 1

Testing a clinical intervention while gathering information on its delivery during the effectiveness trial and/or on its potential for implementation in a real-world situation.

Modest refinements to effectiveness studies are possible that would retain their strength and involve no loss in the ability to achieve their primary goal, whereas simultaneously improving their ability to achieve a key secondary goal; that is, serve as a transition to implementation research. In most cases for Hybrid Type 1, we are advocating process evaluations ( Table 1 ) of delivery/implementation during clinical effectiveness trials to collect valuable information for use in subsequent implementation research trials (hybrid or not). Many potential implementation research questions thus can be addressed, perhaps more comprehensively, accurately and certainly earlier than could be achieved in a sequential “intervention-then-preliminary-implementation” study strategy: What are potential barriers and facilitators to “real-world” implementation of the intervention? What problems were associated with delivering the intervention during the clinical effectiveness trial and how might they translate or not to real-world implementation? What potential modifications to the clinical intervention could be made to maximize implementation? What potential implementation strategies appear promising?

We recommend that the above type of questions should be posed to representatives of relevant stakeholder groups—for example, patients, providers, and administrators. Process evaluation data can also help explain/provide context for summative findings from the clinical effectiveness trial.

Recommended conditions for use: Hybrid 1 designs should be considered under the following conditions: (1) there should be strong face validity for the clinical intervention that would support applicability to the new setting, population, or delivery method in question; (2) there should be a strong base of at least indirect evidence (eg, data from different but associated populations) for the intervention that would support applicability to the new setting, population, or delivery method in question; (3) there should be minimal risk associated with the intervention, including both its direct risk and any indirect risk through replacement of a known adequate intervention. These conditions, to varying degrees, are often found in “research-practice networks” such as the National Institute on Drug Abuse clinical trials network, and Hybrid 1 designs should be particularly attractive for these partnerships.

In addition, there are conditions under which a Hybrid 1 study would seem premature or less feasible—for example, in clinical effectiveness trials with major safety issues, complex comparative effectiveness trials, and “pilot” or very early clinical effectiveness trials. In general, however, we argue that a Hybrid 1 is particularly “low risk” with the potential for high reward given that the implementation research portion is essentially an “add-on” to a routinely designed and powered clinical trial. When moving into the next Hybrid type, there are more complexities to consider and trade-offs to be weighed.

As summarized in Table 4 , a recent Hybrid Type 1 study by Hagedorn et al 30 included a randomized clinical effectiveness trial of contingency management with a mixed-method, multistakeholder process evaluation of the delivery of the intervention. In another example (not found in the Table 4 ), the National Institute on Mental Health-funded “Coordinated Anxiety Learning and Management (CALM)-study” 34 tested the clinical effectiveness of a collaborative care intervention for anxiety disorders while also conducting a multistakeholder qualitative process evaluation. Key research questions in the CALM process evaluation were: (1) what were the facilitators/barriers to delivering the CALM intervention?; (2) what were the facilitators/barriers to sustaining the CALM intervention after the study was completed?; (3) how could the CALM intervention be changed to improve adoption and sustainability?

Hybrid Type 2

Simultaneous testing of a clinical intervention and an implementation intervention/strategy.

This hybrid type is a more direct blending of clinical effectiveness and implementation research aims in support of more rapid translation. In this case, interventions in both the clinical and implementation spheres are tested simultaneously. It is important to note that we are using the term “test” in a liberal manner, meaning that the interventions in question need not all be tested with randomized, strongly powered designs. What makes for a “test” of an intervention here is that at least 1 outcome measure is being used and that at least 1 related hypothesis, however preliminary, is being studied. The nature of randomizations/comparisons and power can vary depending on research needs and conditions. Given the reality of research funding limits, it is likely that some design/power compromises will be necessary in one or both of the intervention tests; however, in the cases of conditions favorable to this hybrid type (see below), such design compromises need not derail progress toward addressing translation gaps/needs in the literature.

This hybrid type is also motivated by the recognition that conventional effectiveness studies often yield estimates of effectiveness that are significantly different (worse) from the estimates of efficacy studies because the effectiveness study is often conducted in “worst case” conditions; that is, with little or no research team support of delivery/implementation, without clear understanding of barriers to fidelity, and without efforts to overcome those barriers. In a Hybrid Type 2 study, where an implementation intervention/strategy of some kind is being tested alongside and in support of a clinical intervention under study, it is possible to create and study a “medium case”/pragmatic set of delivery/implementation conditions versus “best” or “worst” case conditions. Therefore, while speeding translation, it is possible with Hybrid Type 2 designs to provide more valid estimates of potential clinical effectiveness.

Recommended conditions for use: The following conditions are recommended to consider a Hybrid Type 2: (1) there should be strong face validity for the clinical and implementation interventions/strategies that would support applicability to the new setting, population, or delivery/implementation methods in question; (2) there should be at least a strong base of indirect evidence (defined above) for the clinical and implementation interventions/strategies that would support applicability to the new setting, population, or delivery/implementation method in question; (3) there should be minimal risk associated with the clinical and implementation interventions/strategies, including both the direct risk of the interventions and any indirect risk through replacement of known adequate interventions; (4) there should be “implementation momentum” within the clinical system and/or the literature toward routine adoption of the clinical intervention in question. The momentum could come from a number of possible scenarios or factors—for example, strong “indirect” efficacy or effectiveness data; advocacy from patient groups, providers or lawmakers (often in the case of severe clinical consequences/risks from nonaction); and/or health system administrators seeking rapid uptake of an intervention based on the above or other factors, for example, costs. Evidence of such momentum could come from published reports, official policies, or even from discussions with key stakeholders; (5) there should be reasonable expectations that the implementation intervention/strategy being tested is supportable in the clinical and organizational context under study; (6) there is reason to gather more data on the effectiveness of the clinical intervention (eg, it is being provided in a different format or novel setting).

In addition, we have identified other conditions that might be considered to be “ideal” for this hybrid type. These are: (i) strong indirect clinical evidence (see #2 above) comes from either a population or clinical setting reasonably close to the population or setting in question, thereby not necessitating a large clinical effectiveness trial. If the clinical effectiveness study can be of moderate size, additional budget and efforts can be used toward the implementation intervention/strategy and its evaluation; (ii) the clinical intervention and/or implementation intervention/strategy to be tested are not overly complex in terms of changes necessary within the clinic/organization to support it; that is, the testing of clinical and implementation interventions/strategies within the same providers/clinics/systems is not perceived to be, nor actually is overly taxing to participating stakeholders.

As summarized in Table 4 , the Hybrid Type 2 “Enhancing Quality and Utilization in Psychosis study” 31 was an 8-site VA study where 4 sites were randomized to a chronic illness care model for schizophrenia (clinical/delivery system intervention) supported by an implementation strategy (facilitation, quality improvement teams, quality reports, etc.). The study gathered clinical and implementation outcome data at all sites. The investigators recognized a need to test implementation strategies to support recovery-oriented interventions for persons with schizophrenia, as many guidelines and VA directives were encouraging the use of recovery-oriented programs even in the case of less than ideal effectiveness research support. In another example (not in Table 4 ), the “HIV Translating Initiatives for Depression into Effective Solutions study,” 35 human immunodeficiency virus (HIV) patients were randomized to a clinical/delivery system intervention (collaborative care for depression) at 3 VA clinics, whereas the same clinics participated in a nonrandomized, exploratory implementation strategy as well. Although it was clear to the investigators that a patient-level randomized trial of the effectiveness of depression collaborative care in HIV patients was needed (no trials yet in HIV setting), they also recognized that, given the strong evidence of depression collaborative care in primary care settings (similar in scope to many HIV clinics) and momentum in the system for its uptake, it was also timely to use the study to explore an implementation strategy in this setting as well. An additional Hybrid Type 2 design variant (also not in Table 4 ) comes from the “Healthy Bones” study, 36 where both patient-directed and physician-directed interventions for fracture prevention were simultaneously tested in a 2×2 factorial randomized controlled trial. On the basis of the observation that management of osteoporosis and fall prevention was suboptimal and that both patient and provider behaviors needed improvement, the study investors used this design to simultaneously test patient and provider education interventions on a range of outcomes. Although the “clinical” (patient education) and “implementation” (academic detailing) interventions tested were certainly not as complex some of the other examples, perhaps it was this simplicity that allowed for the large factorial design.

Hybrid Type 3

Testing an implementation intervention/strategy while observing/gathering information on the clinical intervention and related outcomes.

A “pure,” nonhybrid implementation study is conducted after an adequate body of evidence has accumulated that clearly establishes the effectiveness of a clinical intervention, and thus clearly supports the appropriateness of costly efforts to try to facilitate better implementation. Sometimes, however, we can and do proceed with implementation studies without completion of the full or at times even a modest portfolio of effectiveness studies beforehand. In such cases, it is common that a prevailing health policy dictates/encourages implementation of a clinical intervention that is, to varying degrees, still in question from an effectiveness perspective. Similar to the cases discussed above with reference to “momentum for implementation,” the situations where health systems actually encourage or attempt implementation of a clinical intervention without the desired clinical effectiveness data base could include the presence of respected consensus guidelines; strong “indirect” efficacy or effectiveness data; advocacy from patient groups, providers or lawmakers (often in the case of the current state of practice and severe clinical consequences/risks from nonaction); and administrators seeking to reduce costs by implementing a cheaper clinical alternative. In these cases, it is, therefore, important to proactively include resources to collect evidence of clinical effectiveness.

In addition, Hybrid Type 3 designs are indicated if it is suspected that the clinical intervention effects might be susceptible to change during implementation in a new setting or under conditions less controlled that in effectiveness trials. Such changes in clinical intervention effectiveness could represent either a vulnerability or an enhancement under implementation conditions compared with effects seen during clinical trials.

Recommended conditions for use: The following conditions are recommended to consider a Hybrid Type 3: (1) there should be strong face validity for the clinical and implementation interventions/strategies that would support generalizability to the new setting, population, or delivery/implementation methods in question; (2) there should be a strong base of indirect evidence (defined above) for the clinical and implementation interventions/strategies that would support generalizability to the new setting, population, or delivery/implementation method in question; (3) there should be minimal risk associated with the clinical and implementation interventions/strategies, including both the direct risk of the interventions and any indirect risk through replacement of known adequate interventions; (4) there should be strong “implementation momentum” in the form of actual mandates or strong encouragement within the clinical system and/or the literature toward routine adoption of the clinical intervention in question; (5) there should be evidence that the implementation intervention/strategy being tested is feasible and supportable in the clinical and organization context under study.

As summarized in Table 4 , the Hybrid Type 3 “Blended-Facilitation” study (Kirchner et al 32 ) is a 16-site implementation trial in VA with 8 sites receiving an implementation facilitation strategy consisting of internal and facilitation (plus numerous implementation tools and aids) to support implementation of integrated primary care and mental health. Internal (to the program sites) and external facilitators use a variety of strategies to facilitate implementation including academic detailing, provider education, local change agent participation, stakeholder engagement at all levels of the organization, performance monitoring and feedback, formative evaluation, and marketing. The comparison sites receive a dissemination/implementation strategy being provided by the VA nationally , as integrated primary care mental health is an officially mandated “best practice.” Some components of what is being “rolled-out” nationally do not have a strong clinical effectiveness research base—for example, use of “generic” mental health care managers (the data support only care managers providing service for individual disorders like depression or specific clusters of disorders like anxiety disorders). Therefore, while the main outcomes for the study are implementation focused, the study is also collecting clinical data from the VA’s automated medical record where possible (eg, scores on routine depression screeners). In another example, the “Implementation of the Hospital to Home (H2H) Health Failure Initiative” (Heidenreich et al 37 ) study is testing an implementation strategy to support uptake of the H2H Initiative (a package of clinical interventions) in multiple facilities while also collecting clinical outcome data. The study randomized 122 VA facilities to intervention and comparison conditions, with intervention facilities receiving a range of implementation interventions, including web-based “kick-off” meetings (education and marketing), toolkit dissemination, and roles for local opinion leaders. Comparison programs are converting to intervention programs after 6 months. Although key outcomes variables related to uptake of H2H are defined for the implementation component (eg, enrollment rates other performance measures), the study is also collecting and comparing key patient outcomes data (mortality and rehospitalization) across intervention and comparison sites.

As we have explored relevant work in the VA and the implementation field in general, we have seen nonsystematic efforts at blending effectiveness and implementation trial elements. Through this hybrid framework we offer guidance to the field and hopefully provide assistance to investigators searching for identifiable design solutions. In addition, we hope to stimulate further thinking and to encourage new design combinations. The hybrid definition and typology offered here must be considered constructs still in evolution. It is important to note that the “boundaries” we have drawn around these hybrid types are not intended to be rigid, and that future work should refine and extend what has been presented here. In addition, we recognize that some of the “recommended conditions for use” of the hybrids are subjective (eg, current definitions of “strong face validity” and “indirect evidence”) and that they will need to be reasoned and argued by investigators on a case-by-case basis at least until additional work refines the definitions and conditions.

Although traditional clinical effectiveness and implementation trials are likely to remain the most common approach to moving a clinical intervention through from efficacy research to public health impact, judicious use of the proposed hybrid designs could speed the translation of research findings into routine practice. However, despite their potential benefits, we recommend that certain conditions should first be met; and, even when desirable, we recognize that hybrids might not always be feasible or affordable within traditional research budget limits. We recommend that future hybrid research seeks to document in both quantitative and qualitative ways the extent and manner in which translation has been sped. As of now, we can only say that these hybrids have the potential to speed and improve translation. Further, the relative speed of translation is not usually included in traditional cost effectiveness analyses, and it would be interesting to explore the potential benefits of hybrid designs from this perspective.

In considering use of a hybrid, it is important to acknowledge the potential “ecological” challenges associated with pursuing such designs. First, researchers from clinical and implementation research backgrounds often do not share concepts, constructs, and vocabulary; more difficult, sometimes the vocabulary is the same but the meanings are different. This makes it somewhat difficult for researchers from different traditions to communicate efficiently and effectively, which could serve as a barrier to collaboration, and perhaps also impede comprehension during research proposal and manuscript reviews. More specifically, lack of reviewer expertise on grant review panels and among journal reviewers and editorial boards relative to emerging concepts and innovations in the field of implementation science can have an inhibitory effect on the development, implementation, and reporting of hybrid studies. Review of hybrid designs requires at least an appreciation of the complexities balancing internal and external validity considerations in such trials, as well as the design trade-offs inherent in structuring such complex protocols and related budgetary needs. Reviews must also, of course, have sufficient technical expertise across members so that, in aggregate, both the clinical intervention and the implementation aspects of the study can be effectively evaluated.

Finally, the same appreciation and expertise required of journal and grant review bodies is required on promotion and tenure committees, although as implementation research and hybrid designs become more widely appreciated, this lack of expertise will diminish—as it has for effectiveness-oriented clinical trials. 4 , 38 – 40 Hybrid studies are typically more complex to execute and thus may be relatively “high risk”; however, the successfully implemented hybrid study will likely pay dividends across both the (a priori) clinical and implementation foci, thus yielding rich data that will be of use both scientifically and in terms of public health impact.

The impetus to blend or explicitly link research traditions in the service of accelerating scientific progress and enhancing public health impact is not at all new, 4 , 38 – 40 and the idea of blending clinical effectiveness and implementation research elements is also not new. As the examples above indicate, “informal” hybrid design trials are already being conducted and reported. The function of this study is both to help the field better organize its thinking and design deliberations concerning these concepts that we felt were not yet clearly articulated and to stimulate further development. The “ecological” challenges noted above will not endure. They can be overcome, like many diffusion of innovation challenges, with education and committed leadership over time.

Acknowledgments

Supported by a research grant for the Department of Veterans Affairs, Health Services Research and Development Service: MNT-05-152 (Pyne, PI) and also funded by a research grant from the National Institute on Drug Abuse: K01 DA15102 (Curran, PI).

The authors declare no conflict of interest.

• 1. Institute of Medicine. Crossing the Quality Chasm: A New Health System for the 21st Century. Washington, DC: Institute of Medicine of the National Academics Press; 2001. [ PubMed ] [ Google Scholar ]
• 2. Grol R, Wensing M, Eccles M. Improving Patient Care: The Implementation of Change in Clinical Practices. Toronto: Elsevier; 2005. [ Google Scholar ]
• 3. Stetler CB, McQueen L, Demakis J, et al. An organizational framework and strategic implementation for system-level change to enhance research-based practice: QUERI Series. Implement Sci. 2008;3:30. doi: 10.1186/1748-5908-3-30. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 4. Glasgow RE, Lictenstein E, Marcus AC. Why don’t we see more translation of health promotion research to practice? Rethinking the efficacy-to-effectiveness transition. Am J Public Health. 2003;93:1261–1267. doi: 10.2105/ajph.93.8.1261. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 5. Shojania KG, Ranji SR, Shaw LK, et al. Closing the Quality Gap: A Critical Analysis of Quality Improvement Strategies (Vol 2: Diabetes Care) Rockville, MD: Agency for Healthcare Research and Quality; 2004. [ PubMed ] [ Google Scholar ]
• 6. Bravata DM, Sundaram V, Lewis R, et al. Closing the Quality Gap: A Critical Analysis of Quality Improvement Strategies (Vol 5: Asthma Care) Rockville, MD: Agency for Healthcare Research and Quality; 2007. [ PubMed ] [ Google Scholar ]
• 7. Walsh J, McDonald KM, Shojania KG, et al. Closing the Quality Gap: A Critical Analysis of Quality Improvement Strategies (Vol 3: Hypertension Care) Rockville, MD: Agency for Healthcare Research and Quality; 2005. [ PubMed ] [ Google Scholar ]
• 8. Carroll KM, Rounsaville BJ. Bridging the gap: a hybrid model to link efficacy and effectiveness research in substance abuse treatment. Psychiatr Serv. 2003;54:333–339. doi: 10.1176/appi.ps.54.3.333. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 9. Ranji SR, Steinman MA, Sundaram V, et al. Closing the Quality Gap: A Critical Analysis of Quality Improvement Strategies (Vol 4: Antibiotic Prescribing Behavior) Rockville, MD: Agency for Healthcare Research and Quality; 2006. [ PubMed ] [ Google Scholar ]
• 10. Freemantle N, Eccles M, Wood J, et al. A randomized trial of evidence-based outreach (EBOR) rationale and design. Control Clin Trials. 1999;20:479–492. doi: 10.1016/s0197-2456(99)00023-9. [ DOI ] [ PubMed ] [ Google Scholar ]
• 11. Cochrane LJ, Olson CA, Murray S, et al. Gaps between knowing and doing: understanding and assessing the barriers to optimal health care. J Contin Educ Health Prof. 2007;27:94–102. doi: 10.1002/chp.106. [ DOI ] [ PubMed ] [ Google Scholar ]
• 12. Fruth SJ, Veld RD, Despos CA, et al. The influence of a topic-specific, research-based presentation on physical therapists’ beliefs and practices regarding evidence-based practice. Physiother Theory Pract. 2010;26:537–557. doi: 10.3109/09593980903585034. [ DOI ] [ PubMed ] [ Google Scholar ]
• 13. Caban MD, Rand CS, Powe NR, et al. Why don’t physicians follow clinical practice guidelines? A framework for improvement. JAMA. 1999;282:1458–1465. doi: 10.1001/jama.282.15.1458. [ DOI ] [ PubMed ] [ Google Scholar ]
• 14. Reschovsky JD, Hadley J, Landon BE. Effects of compensation methods and physician group structure on physicians’ perceived incentives to alter services to patients. Health Serv Res. 2006;41:1200–1220. doi: 10.1111/j.1475-6773.2006.00531.x. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 15. Racine DP. Reliable effectiveness: a theory on sustaining and replicating worthwhile innovations. Adm Policy Ment Health. 2006;33:356–387. doi: 10.1007/s10488-006-0047-1. [ DOI ] [ PubMed ] [ Google Scholar ]
• 16. Damschroder LJ, Aron DC, Keith RE, et al. Fostering implementation of health services research findings into practice: a consolidated framework for advancing implementation science. Implement Sci. 2009;4:50. doi: 10.1186/1748-5908-4-50. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 17. Tunis SR, Stryer DB, Clancey CM. Increasing the value of clinical research for decision making in clinical and health policy. JAMA. 2003;290:1624–1632. doi: 10.1001/jama.290.12.1624. [ DOI ] [ PubMed ] [ Google Scholar ]
• 18. March JS, Silva SG, Comptom S, et al. The case for practical clinical trials in psychiatry. Am J Psychiatry. 2005;162:836–846. doi: 10.1176/appi.ajp.162.5.836. [ DOI ] [ PubMed ] [ Google Scholar ]
• 19. Wells KB. Treatment research at the crossroads: the scientific interface of clinical trials and effectiveness research. Am J of Psychiatry. 1999;156:5–10. doi: 10.1176/ajp.156.1.5. [ DOI ] [ PubMed ] [ Google Scholar ]
• 20. Proctor EK, Landsverk J, Aarons G, et al. Implementation research in mental health services: an emerging science with conceptual, methodological, and training challenges. Adm Policy Ment Health. 2009;36:24–34. doi: 10.1007/s10488-008-0197-4. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 21. Stetler CB, Legro MW, Wallance CM, et al. The role of formative evaluation in implementation research and the QUERI experience. J Gen Intern Med. 2006;21:S1–S8. doi: 10.1111/j.1525-1497.2006.00355.x. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 22. Stetler CB, Mittman BS, Francis J. Overview of the VA Quality Enhancement Research Initiative (QUERI) and QUERI Theme Articles: QUERI Series. Implement Sci. 2008;3:8. doi: 10.1186/1748-5908-3-8. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 23. Demakis JG, McQueen L, Kizer KW, et al. Quality Enhancement Research Initiative (QUERI): a collaboration between research and clinical practice. Med Care. 2000;38:17–25. [ PubMed ] [ Google Scholar ]
• 24. Bauer MS, Williford WO, Dawson EE, et al. Principals of effectiveness trials and their implementation in VA Cooperative Study #430: Reducing the efficacy-effectiveness gap in bipolar disorder. J Affect Disord. 2001;67:61–78. doi: 10.1016/s0165-0327(01)00440-2. [ DOI ] [ PubMed ] [ Google Scholar ]
• 25. Sox HC. Comparative effectiveness research: a progress report. Ann Intern Med. 2010;153:469–472. doi: 10.7326/0003-4819-153-7-201010050-00269. [ DOI ] [ PubMed ] [ Google Scholar ]
• 26. Atkins D. QUERI and implementation research: emerging from adolescence into adulthood: QUERI series. Implement Sci. 2009;4:12. doi: 10.1186/1748-5908-4-12. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 27. Bauer MS, McBride L, Williford WO, et al. for the CSP #430 Study Team. Collaborative care for bipolar disorder, Part I: intervention and implementation in a randomized effectiveness trial. Psychiatric Services. 2006a;57:927–936. doi: 10.1176/ps.2006.57.7.927. [ DOI ] [ PubMed ] [ Google Scholar ]
• 28. Bauer MS, McBride L, Williford WO, et al. for the CSP #430 Study Team. Collaborative care for bipolar disorder, Part II: impact on clinical outcome, function, and costs. Psychiatric Services. 2006b;57:937–945. doi: 10.1176/ps.2006.57.7.937. [ DOI ] [ PubMed ] [ Google Scholar ]
• 29. Bauer MS, Biswas K, Kilbourne AM. Enhancing multi-year guideline concordance for bipolar disorder through collaborative care. Am J Psychiatry. 2009;166:1244–1250. doi: 10.1176/appi.ajp.2009.09030342. [ DOI ] [ PubMed ] [ Google Scholar ]
• 30. Hagedorn H, Noorbaloochi S, Rimmele C, et al. The Rewarding Early Abstinence and Treatment Participation (REAP) Study. Presented at Enhancing Implementation Science in VA; Denver, CO. 2010. [ Google Scholar ]
• 31. Brown AH, Cohen AN, Chinman MJ, et al. EQUIP: implementing chronic care principles and applying formative evaluation methods to improve care for schizophrenia: QUERI Series. Implement Sci. 2008;3:9. doi: 10.1186/1748-5908-3-9. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 32. Kirchner JE, Ritchie M, Curran G, et al. Enhancing Implementation Science meeting sponsored by Department of Veterans Affairs Quality Enhancement Research Initiative. Phoenix: AZ: 2011. Facilitating: Design, Using, and Evaluating a Facilitation Strategy. [ Google Scholar ]
• 33. Lukas CV, Engle RL, Holmes SK, et al. Strengthening organizations to implement evidence-based clinical practices. Healthcare Manag Rev. 2010;35:235–245. doi: 10.1097/HMR.0b013e3181dde6a5. [ DOI ] [ PubMed ] [ Google Scholar ]
• 34. Roy-Byrne P, Craske MG, Sullivan G, et al. Delivery of evidence-based treatment for multiple anxiety disorders in primary care. JAMA. 2010;303:1921–1928. doi: 10.1001/jama.2010.608. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• 35. Pyne JM, Fortney JC, Curran GC, et al. Effectiveness of collaborative care for depression in human immunodeficiency virus clinics. Arch Intern Med. 2011;171:23–31. doi: 10.1001/archinternmed.2010.395. [ DOI ] [ PubMed ] [ Google Scholar ]
• 36. Solomon DH, Brookhart MA, Polinski J, et al. Osteoporosis action: design of the Healthy Bones project trial. Contemp Clin Trials. 2005;26:78–94. doi: 10.1016/j.cct.2004.11.012. [ DOI ] [ PubMed ] [ Google Scholar ]
• 37. Heidenreich, et al. http://www.queri.research.va.gov/chf/products/h2h .
• 38. Zerhouni E. The NIH Roadmap. Science. 2003;302:63–72. doi: 10.1126/science.1091867. [ DOI ] [ PubMed ] [ Google Scholar ]
• 39. Wells K, Miranda J, Bruce ML, et al. Bridging community intervention and mental health services research. Am J Psychiatry. 2004;161:955–963. doi: 10.1176/appi.ajp.161.6.955. [ DOI ] [ PubMed ] [ Google Scholar ]
• 40. Brown CH, Ten Have TR, Jo B, et al. Adaptive designs for randomized trials in public health. Annu Rev Public Health. 2009;30:1–25. doi: 10.1146/annurev.publhealth.031308.100223. [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
• View on publisher site
• PDF (133.1 KB)
• Collections

Similar articles

Cited by other articles, links to ncbi databases.

• Download .nbib .nbib
• Format: AMA APA MLA NLM

Add to Collections

Europe PMC requires Javascript to function effectively.

Either your web browser doesn't support Javascript or it is currently turned off. In the latter case, please turn on Javascript support in your web browser and reload this page.

Search life-sciences literature (45,050,293 articles, preprints and more)

• Free full text
• Citations & impact
• Similar Articles

Hybrid Experimental Designs for Intervention Development: What, Why, and How.

Author information, affiliations.

• Nahum-Shani I 1
• Walton MA 3
• Dempsey W 4

ORCIDs linked to this article

• Nahum-Shani I | 0000-0001-6138-9089
• Dziak JJ | 0000-0003-0762-5495

Advances in Methods and Practices in Psychological Science , 01 Jul 2022 , 5(3) https://doi.org/10.1177/25152459221114279   PMID: 36935844  PMCID: PMC10024531

Abstract 

Free full text .

Hybrid Experimental Designs for Intervention Development: What, Why, and How

Inbal nahum-shani.

1 Institute for Social Research, University of Michigan, Ann Arbor, Michigan;

John J. Dziak

2 Prevention Research Center, The Pennsylvania State University, State College, Pennsylvania;

Maureen A. Walton

3 Department of Psychiatry and Addiction Center, Injury Prevention Center, University of Michigan, Ann Arbor, Michigan;

Walter Dempsey

4 School of Public Health and Institute for Social Research, University of Michigan, Ann Arbor, Michigan

Author Contributions

• Associated Data

Advances in mobile and wireless technologies offer tremendous opportunities for extending the reach and impact of psychological interventions and for adapting interventions to the unique and changing needs of individuals. However, insufficient engagement remains a critical barrier to the effectiveness of digital interventions. Human delivery of interventions (e.g., by clinical staff) can be more engaging but potentially more expensive and burdensome. Hence, the integration of digital and human-delivered components is critical to building effective and scalable psychological interventions. Existing experimental designs can be used to answer questions either about human-delivered components that are typically sequenced and adapted at relatively slow timescales (e.g., monthly) or about digital components that are typically sequenced and adapted at much faster timescales (e.g., daily). However, these methodologies do not accommodate sequencing and adaptation of components at multiple timescales and hence cannot be used to empirically inform the joint sequencing and adaptation of human-delivered and digital components. Here, we introduce the hybrid experimental design (HED)—a new experimental approach that can be used to answer scientific questions about building psychological interventions in which human-delivered and digital components are integrated and adapted at multiple timescales. We describe the key characteristics of HEDs (i.e., what they are), explain their scientific rationale (i.e., why they are needed), and provide guidelines for their design and corresponding data analysis (i.e., how can data arising from HEDs be used to inform effective and scalable psychological interventions).

Advances in digital technologies (e.g., mobile and wearable devices) have created unprecedented opportunities to extend the reach and impact of psychological interventions. Interventions that leverage automated software tools are relatively inexpensive and can deliver in-the-moment support ( Goldstein et al., 2017 ; Huh et al., 2020 ). However, insufficient engagement (i.e., the investment of energy in a focal task or stimulus) remains a critical barrier to the effectiveness of digital interventions ( Nahum-Shani, Shaw, et al., 2022 ). Human delivery of interventions (e.g., by clinical staff) can be more engaging ( Ritterband et al., 2009 ; Schueller et al., 2017 ) but potentially more expensive and burdensome. Hence, integrating digital- and human-delivered intervention components requires balancing effectiveness against scalability and sustainability ( Schueller et al., 2017 ; Wentzel et al., 2016 ).

The capacity to sequence and adapt intervention delivery to the changing needs of individuals is viewed as an important innovation in psychological science ( Kitayama, 2021 ; Koch et al., 2021 ; Lattie et al., 2022 ). Interventions are considered “adaptive” if they use time-varying (i.e., dynamic) information about the individual (e.g., location, emotions) to modify the type or intensity of interventions over time. Human-delivered intervention components are typically adapted at relatively slow timescales (e.g., weekly, monthly). For example, the adaptive drug court program for drug-using offenders ( Marlowe et al., 2012 ) starts with standard substance use counseling and then every month uses information about the participant’s response status to decide whether to enhance the intensity of the counseling sessions. Here, the adaptation occurs monthly. Digital-intervention components, on the other hand, are typically adapted at a much faster timescale (e.g., every minute, daily). For example, Sense2Stop ( Battalio et al., 2021 ) is a mobile intervention that uses information about the participant’s stress, which is collected every minute via a wearable device, to decide whether to deliver a push notification suggesting a brief stress-management exercise. Here, the adaptation occurs every minute.

Existing experimental designs and related data-analytic methods can be used to answer questions either about how to best employ components that are sequenced and adapted at relatively slow timescales or about how to best employ components that are sequenced and adapted at much faster timescales. However, these methodologies do not accommodate sequencing and adaptation of components at multiple timescales and hence cannot be used to answer scientific questions about how to best integrate human-delivered and digital components. To close this gap, we introduce the hybrid experimental design (HED)—a new experimental approach that can be used to answer scientific questions about the construction of psychological interventions in which human-delivered and digital components are integrated and adapted at multiple timescales. HEDs enable researchers to sequentially randomly assign study participants at multiple timescales, thereby providing data that can answer questions about how to best combine components that are sequenced and adapted at multiple timescales.

The goal of this article is to explain why HEDs are needed, what their key characteristics are, and how they can inform psychological interventions. To achieve these goals, we first explain how standard adaptive interventions (ADIs) typically guide the adaptation of intervention components at relatively slow timescales. We then describe how the sequential, multiple-assignment, randomized trial (SMART)—an experimental design involving sequential randomizations at relatively slow timescales—can be used to answer scientific questions about constructing ADIs. Next, we explain how just-in-time adaptive interventions (JITAIs) typically guide the adaptation of intervention components at relatively fast timescales. This is followed by describing how the microrandomized trial (MRT)—an experimental design involving sequential random assignments at relatively fast timescales—can be used to answer scientific questions about constructing JITAIs. Building on the work described above, we define multimodality adaptive interventions (MADIs) as an intervention delivery framework in which human-delivered and digital components are integrated and adapted at multiple timescales, slow and fast. Finally, we define and describe key features of the HED—an experimental design involving sequential randomizations at multiple timescales. We explain how HEDs can be used to answer scientific questions about constructing MADIs. Throughout, we use an example that is based on existing research but modified for illustrative purposes. Key terms and definitions are summarized in Table 1 .

Definitions of Key Terms

An ADI is an intervention-delivery framework that typically guides the adaptation of human-delivered components at timescales of weeks or months ( Collins, 2018 ; Murphy et al., 2007 ). These interventions are becoming increasingly popular across various domains of psychological sciences, including health ( Czajkowski & Hunter, 2021 ; Spring, 2019 ), clinical ( Patrick et al., 2021 ; Pelham et al., 2016 ), educational ( Chow & Hampton, 2022 ; Majeika et al., 2020 ), and organizational ( Eden, 2017 ; Howard & Jacobs, 2016 ) psychology. In practice, an ADI is a protocol that specifies how tailoring variables (i.e., time-varying information about the individual’s progress and status) should be used by practitioners (e.g., therapists, teachers, coaches) to decide whether and how to modify intervention components at each of a few decision points (i.e., points in time in which intervention decisions should be made) during the course of treatment. ADIs are designed to achieve a distal outcome (i.e., a long-term goal) by achieving proximal outcomes, which are the short-term goals the adaptation is intended to achieve. The proximal outcomes are mechanisms of change (i.e., mediators) through which the adaptation can help achieve the distal outcome ( Nahum-Shani & Almirall, 2019 ).

The example in Figure 1 is a hypothetical ADI to prevent substance use and violent behavior among adolescents visiting the emergency department (ED). This example is based on an existing research project ( Bernstein et al., 2022 ) but modified for illustrative purposes. In this example, all participants are provided a single human-delivered session during an ED visit, focused on reducing risks and increasing resilience, plus a digital intervention that includes daily messages (e.g., protective behavioral strategies, alternative leisure activities). The tailoring variable, response status, is assessed 4 weeks after discharge, and youths classified as early nonresponders (i.e., individuals reporting substance use or physical aggression) are offered human-delivered (remote) coaching in addition to the digital intervention. Individuals classified as early responders (i.e., youths reporting no substance use and no physical aggression) continue with the digital intervention. This intervention is “adaptive” because it uses time-varying information (here, about the individual’s response status) to decide whether and how to intervene subsequently (here, whether to add human coaching). This intervention includes decision points at Weeks 0 (ED visit) and 4 because the goal is to address conditions (i.e., early signs of nonresponse) that tend to unfold at a relatively slow timescale (here, over several weeks).

An adaptive intervention (ADI) to prevent substance use and violent behavior among adolescents visiting the emergency department (ED).

Investigators interested in developing ADIs often have scientific questions about how to best construct these interventions. As an example, suppose the goal is to determine (a) whether it is better (e.g., in terms of reduction in substance use by Week 16) to augment the single session provided in the ED with a digital intervention alone or with both a digital intervention and (human-delivered) coaching and (b) whether it is better to step up the intensity of the initial intervention for participants who show signs of nonresponse by Week 4.

The SMART ( Lavori & Dawson, 2000 ; Murphy, 2005 ) is an experimental design that is being used extensively in psychological research (for review of studies, see Ghosh et al., 2020 ) to inform the development of ADIs. At each ADI decision point, participants are randomly assigned among a set of intervention options. For example, the hypothetical SMART in Figure 2 can be used to answer the questions outlined above. This design involves two stages of random assignment that correspond to two decision points in the ADI of interest. First, youths in the ED are randomly assigned (.5 probability) to augment the single session with either a digital intervention alone or combined with coaching. Second, at Week 4, nonresponders (i.e., youths reporting substance use or physical aggression) are randomly assigned again (.5 probability) to either continue with the initial intervention or step up to a more intense intervention; responders (i.e., youths reporting no substance use and no physical aggression) continue with the initial intervention. Suppose the primary distal outcome is the number of substance use (e.g., alcohol, marijuana use) days measured at Week 16. Note that the design in Figure 2 is considered a “prototypical SMART” ( Nahum-Shani et al., 2020 ), that is, the SMART includes two stages of random assignment, each stage involves random assignment to two ADI options, early response status is determined at a single point in time, and only nonresponders get randomly assigned again to subsequent options (i.e., second-stage random assignment is restricted to nonresponders).

An example sequential, multiple-assignment, randomized trial to empirically develop an adaptive intervention (ADI) for preventing substance use and violent behavior among adolescents visiting the emergency department (ED).

The analyses for addressing the aforementioned scientific questions (whether it is better to augment the single session provided in the ED with a digital intervention alone or with both a digital intervention and (human-delivered) coaching and whether it is better to step up the intensity of the initial intervention for participants who show signs of nonresponse by Week 4) leverage outcome information across multiple experimental conditions ( Collins et al., 2014 ; Nahum-Shani et al., 2012a ). Specifically, the first question can be answered by comparing the mean outcome across all the conditions in which participants were offered the digital intervention alone initially ( Fig. 2, A – C ) to the mean outcome across all the conditions in which participants were offered the digital intervention combined with coaching initially ( Fig. 2, D – F ). Note that this comparison would involve using outcome data from the entire sample to estimate the effect, which can be viewed as the main effect of the initial components averaging over the subsequent components for responders and nonresponders ( Nahum-Shani, Dziak, & Wetter, 2022 ; Nahum-Shani et al., 2020 ). The second question can be answered by comparing the mean outcome across the two experimental conditions in which nonresponders were offered the step-up subsequently ( Fig. 2 , ​ ,B B and ​ andE) E ) to the mean outcome across the two conditions in which nonresponders continued with the initial intervention ( Fig. 2 , ​ ,C C and ​ andF). F ). Note that this comparison would involve using outcome data from the entire sample of nonresponders to estimate the effect, which can be viewed as the main effect of the subsequent components among nonresponders averaging over the initial components ( Nahum-Shani, Dziak, & Wetter, 2022 ; Nahum-Shani et al., 2020 ).

The multiple, sequential, random assignments in this SMART yield four “embedded” ADIs ( Table 2 ). One of these ADIs, represented by Cells A and B, is described in Figure 1 . Data from SMARTs can be used to compare embedded ADIs and to answer a wide variety of scientific questions beyond the main effects of the first- and second-stage components (e.g., Nahum-Shani et al., 2012b , 2020 ). The extant literature highlights the efficiency of SMARTs in achieving statistical power for addressing scientific questions about building ADIs ( Collins et al., 2014 ; Murphy, 2005 ; Nahum-Shani et al., 2012a ).

Four ADIs Embedded in the SMART in Figure 2

Note: ADI = adaptive intervention; ED = emergency department.

JITAIs typically guide the sequencing and adaptation of digital-intervention components. These interventions are becoming increasingly popular across various domains of psychological sciences, including health ( Conroy et al., 2020 ; Nahum-Shani, Rabbi, et al., 2021 ), clinical ( Comer et al., 2019 ; Coppersmith, 2022 ), educational ( Cook et al., 2018 ), and organizational ( Valle et al., 2020 ) psychology. Leveraging powerful digital technologies, a JITAI is a protocol that specifies how rapidly changing information about the individual’s internal state (e.g., mood, substance use) and context (e.g., geographical location, presence of other people) should be used in practice to decide whether and how to deliver intervention content (e.g., feedback, motivational messages, behavioral or cognitive strategies) in real time in the individual’s natural environment ( Nahum-Shani et al., 2015 , 2018 ). For example, suppose the delivery of messages in the digital intervention described above follows the JITAI in Figure 3 . Specifically, the mobile device prompts participants to provide information such as their stress and loneliness via ecological momentary assessments (EMAs) and tracks their physical position via GPS. If this combined information indicates high risk for substance use during the day, then a message would be sent in the evening recommending a protective behavioral strategy. Otherwise, no message would be delivered. This intervention is adaptive because it uses time-varying information (here, about the individual’s risk status) to decide whether and how to intervene subsequently (here, whether to deliver a message). This intervention includes decision points every day because the goal is to address conditions (i.e., short-term risk for substance use) that unfold at a relatively fast timescale (here, daily).

Just-in-time adaptive intervention (JITAI) to guide the delivery of daily messages for adolescents visiting the emergency department.

Investigators interested in developing JITAIs often have scientific questions about how to best construct these interventions. As an example, suppose the goal is to determine (a) whether it is beneficial (e.g., in reducing next-day substance use) on average to deliver a daily message and (b) under what conditions (e.g., level of risk) providing a daily message would be beneficial in reducing next-day substance use.

The MRT ( Qian et al., 2022 ) is an experimental design to inform the development of JITAIs. MRTs are experiencing rapid uptake in psychological research despite being relatively new ( Figueroa et al., 2021 ; Valle et al., 2020 ). At each JITAI decision point, participants are randomly assigned among a set of intervention options. The MRT is conceptually related to the SMART because it also includes sequential random assignments. However, the MRT is designed to provide the empirical basis for constructing JITAIs, which involve adaptation at relatively fast timescales. Hence, an MRT involves sequential random assignments at a relatively fast timescale—participants are randomly assigned to different intervention options hundreds or even thousands of times over the course of the experiment.

For example, the hypothetical MRT in Figure 4 (which is based on Coughlin et al., 2021 ) can be used to answer the two questions outlined above. This MRT employs random assignments daily over 16 weeks (i.e., 112 random assignments): Participants are randomly assigned every day (in the evening) with .5 probability to either a message delivery or no message delivery. Before the random assignments, individuals are prompted on their mobile device to provide information such as their stress, mood, and daily substance use via EMAs. In addition, the mobile device tracks their physical position via GPS, and data are collected about the individual’s response to prior messages. Suppose the primary proximal outcome is the number of drinks on the next day.

An example microrandomized trial to empirically develop a digital just-in-time adaptive intervention for preventing substance use and violent behavior among adolescents visiting the emergency department. EMA = ecological momentary assessment; R = random assignment.

Similar to the SMART, the MRT makes extremely efficient use of study participants to answer questions about building a JITAI. This efficiency is facilitated by capitalizing on both between-subjects and within-subjects contrasts in the proximal outcome ( Qian et al., 2022 ). For example, consider the first question above, in which the proximal outcome is the number of drinks on the next day. This proximal outcome is assessed following each random assignment. Hence, this question can be answered by comparing two means: (a) the average number of next-day drinks when a message was delivered on a given day and (b) the average number of next-day drinks when a message was not delivered on a given day. This difference can be estimated by pooling data across all study participants and also across all decision points in the trial ( Qian et al., 2022 ). This is an estimate of the (causal) main effect of delivering (vs. not delivering) a daily message, in terms of the proximal outcome.

The second question can be answered by investigating whether the difference between the two means described above varies depending on self-reported or sensor-based information collected before random assignment. For example, the data can be used to investigate whether the level of risk before random assignment moderates the causal effect of delivering (vs. not delivering) a message on next-day number of drinks. As before, this analysis would use data across all study participants and across all decision points in the trial ( Qian et al., 2022 ). Estimates of the difference in next-day number of drinks between delivering versus not delivering a message at different levels of risk (e.g., low, moderate, high) can be used to further identify the specific level or levels at which delivering (vs. not delivering) a message would be most beneficial.

Suppose an investigator would like to integrate the ADI in Figure 1 with the JITAI in Figure 3 . Specifically, the goal is to employ the JITAI in Figure 3 as part of the digital-intervention component mentioned in Figure 1 . Figure 5 provides an example in which at program entry, all participants are provided a single (human-delivered) session and a digital intervention delivers a daily message only if momentary risk is high. Response status is assessed 4 weeks after discharge on the basis of self-reported substance use and physical aggression. Human-delivered coaching is added to individuals classified as nonresponders at Week 4, whereas individuals classified as responders continue with the initial intervention. The example in Figure 5 is a MADI—an intervention in which human-delivered and digital components are integrated and adapted at multiple timescales. Although this is the first article to formally define MADIs, there is a growing interest in developing psychological interventions that involve adaptation of human-delivered and digital components at multiple timescales (e.g., Belzer et al., 2018 ; Czyz et al., 2021 ; Patrick et al., 2021 ).

A multimodality adaptive intervention to guide the delivery of human coaching and digital messages for adolescents visiting the emergency department (ED).

The construction of MADIs requires knowledge of how best to combine human-delivered and digital components that are adapted at multiple timescales. These questions are critical given that each decision regarding the integration between digital and human-delivered components (e.g., what, when, how much, for whom) represents a trade-off between benefits and drawbacks ( Mohr et al., 2011 ; Schueller et al., 2017 ). For example, adding (human) coaching for nonresponders may increase engagement with the digital messages but may increase participant burden and intervention cost; intensifying the delivery of digital messages may help address sudden shifts in risk between coaching sessions but may increase habituation to the messages. Hence, an important step in building an effective and scalable integration between human-delivered and digital components is to ensure they are designed synergistically so that the effect of the intervention as a whole is expected to be greater than the sum of effects of the individual components.

Existing experimental approaches address scientific questions about building ADIs (e.g., the SMART) or JITAIs (e.g., the MRT) but not about their integration. Investigators interested in developing interventions that adapt to the changing needs of individuals at multiple timescales must currently settle for addressing questions about the sequencing and adaptation of components at each timescale separately. This compartmentalization represents a major barrier to the effective integration of human-delivered and digital components. Hence, we introduce a new experimental approach that will enable investigators to answer questions about the interplay between intervention components that are sequenced and adapted at multiple timescales.

HED is a type of experimental design that can aid in the development of MADIs. It is a flexible random-assignment trial in which participants can be sequentially randomly assigned to ADI options and to JITAI options at different timescales appropriate for each. Suppose investigators would like to answer the following questions about the development of the MADI in Figure 5 . First, does the proximal impact of daily (digital) messages on next-day number of drinks vary between starting with the digital intervention alone versus the digital intervention combined with (human) coaching ( Table 3 , A2)? Second, does the impact of starting with coaching (vs. digital alone) on substance use reduction at Week 16 vary by the intensity (i.e., the rate) of digital messages delivered ( Table 4 , B3)? These questions concern synergies between human-delivered (coaching) and digital (messages) components that are sequenced and adapted at different timescales (after 4 weeks vs. daily).

Questions About Effects of JITAI Options on a Proximal Outcome (e.g., Next-Day Number of Drinks)

Note: JITAI = just-in-time adaptive intervention; ADI = adaptative intervention.

Questions About Effects of ADI Options on a Distal Outcome (e.g., Week 16 Substance Use)

Note: ADI = adaptative intervention; JITAI = just-in-time adaptive intervention.

The experimental design in Figure 6 can provide data for addressing such questions. This design integrates the SMART in Figure 2 with the MRT in Figure 4 . Specifically, participants are randomly assigned at two ADI decision points (here, at Week 0 and Week 4) to ADI options. These sequential randomizations yield four embedded ADIs ( Table 2 ), similar to the SMART in Figure 2 . In addition, all participants are microrandomly assigned at JITAI decision points (here, every day) during the 16 weeks to either a message delivery or no message delivery. That is, microrandom assignments are embedded in Cells A through F in Figure 6 and hence in each embedded ADI. Tables 3 and ​ and4 4 provide examples of scientific questions about building a MADI that can be answered with data from the HED in Figure 6 . Appendix A in the Supplemental Material available online provides regression models for analyzing the data to answer each question.

An example hybrid experimental design to empirically develop a multimodality adaptive intervention for preventing substance use and violent behaviors among adolescents visiting the emergency department (ED). EMA = ecological momentary assessment; R = random assignment.

Similar to the SMART and the MRT, the HED makes efficient use of study participants to answer questions about building MADIs. For example, consider Question A1 ( Table 3 ), which concerns the proximal impact (on next-day number of drinks) of delivering (vs. not delivering) a daily message averaging over ADI options. This question can be answered by estimating the causal effect of delivering (vs. not delivering) a daily message in terms of next-day number of drinks on average across all study participants, across all JITAI decision points, and across first- and second-stage ADI options. This effect can be viewed as the proximal “main effect” of delivering (vs. not delivering) a message, averaging over ADI options.

Now consider Question A2 ( Table 3 ), which concerns whether the proximal impact on next-day number of drinks of delivering (vs. not delivering) a daily message varies depending on whether coaching was offered initially (vs. the digital intervention alone). This question can be answered by comparing the causal effect of delivering (vs. not delivering) a message on next-day number of drinks between the two initial ADI options. This corresponds to the interaction between the JITAI options and the first-stage ADI options in terms of the proximal outcome. As before, this interaction would be estimated by using data across all study participants and across all JITAI decision points.

Next, consider Question B1 ( Table 4 ), which concerns the distal impact (on Week 16 substance use) of starting with coaching (vs. digital intervention alone), averaging over JITAI options. This question can be answered by using Week 16 outcome information from all study participants. Specifically, this would involve comparing substance use at Week 16 between participants who started with coaching and participants who started with the digital intervention alone, collapsing over the delivery (vs. no delivery) of a daily message at JITAI decision points. This can be viewed as the main effect of the first-stage ADI options on the distal outcome, provided that the daily messages are delivered with .5 probability.

Finally, consider Question B3 ( Table 4 ), which concerns whether the distal impact (on Week 16 substance use) of starting with coaching (vs. digital alone) varies by the intensity (i.e., rate) of digital messages delivered. Note that the random assignments to JITAI options (message vs. no message) with .5 probability at each JITAI decision point generate a distribution across participants in the number of messages delivered in practice over the course of the study. Although the values of this distribution are tightly clustered around the mean (because of the central limit theorem), investigators might still be interested in using this data to explore whether the causal effect of starting with coaching (vs. digital alone) on Week 16 substance use varies between different rates of messages delivered across the 16-week study. This corresponds to an interaction between the first-stage ADI options and the average JITAI options in terms of the distal outcome. As before, this interaction would be estimated by using data across all study participants and across all JITAI decision points.

Appendix B in the Supplemental Material describes the results of Monte Carlo simulation studies showing that with reasonable sample sizes (e.g., 100–200 participants), adequate statistical power can be achieved for addressing Questions A1 through A4 ( Table 3 ) and B1 and B2 ( Table 4 ) with data from a HED such as the one in Figure 6 . As should be expected, power was much lower for questions that concern the rate of JITAI options ( Table 4 , B3 and B4) because the values of this variable are tightly clustered around the mean. A satisfactory power for questions involving the rate of JITAI options would require a different HED whereby the random-assignment probabilities systematically vary between participants. For example, some participants might be assigned to have daily messages delivered with 0.4 probability and others with 0.6, thus creating an added initial ADI factor that influences the JITAI component delivery. Nonetheless, data from the HED in Figure 6 can still provide some useful information about the intensity of message delivery on an exploratory basis that can inform hypothesis generation.

• Practical Steps for Planning a HED

In this section, we suggest pragmatic steps and available resources that researchers can use to implement the HED approach in their own research.

Step 1: develop a working model

This step involves compiling existing empirical evidence and practical considerations into a working model that describes how the candidate MADI being developed may operate. Both the ADI elements and the JITAI elements of the hybrid intervention need to be considered.

The ADI elements include the decision points, intervention options, and tailoring variables. It will also be necessary to decide the thresholds or levels of the tailoring variables that differentiate between conditions under which different ADI options should be delivered; this includes planning for situations in which information about the tailoring variable is not available in practice (see Murphy & McKay, 2004 ; Roberts et al., 2021 ). These decisions can be informed by existing literature and empirical evidence and by consideration of standard clinical practice, expert opinion, or experience. Of course, some important questions will remain unanswered, hence the need for the random-assignment trial (see Step 2). Recommended reading includes literature that describes the motivation for ADIs, their key elements, and guidelines for their design (e.g., Collins et al., 2004 ; Nahum-Shani & Almirall, 2019 ).

Similar elements must be considered for the JITAI, including the JITAI decision points, intervention options, tailoring variables, and the thresholds/levels of the tailoring variables that differentiate between conditions in which different JITAI options should be delivered. Recommended reading includes literature that describes the motivation for JITAIs, their key elements, and guidelines for their design ( Nahum-Shani et al., 2015 , 2018 ).

Step 2: specify scientific questions

Scientific questions that motivate a HED can be expressed in terms of the proximal and/or distal effects of different intervention options. Questions about proximal effects of JITAI options, such as the difference between JITAI options in terms of a proximal outcome (e.g., next-day number of drinks), may concern either their main effects, averaging over ADI options (e.g., Table 3 , A1), or else their interactions with ADI options (e.g., Table 3 , A2–A4). Likewise, the distal effects of ADI options (i.e., the difference between ADI options in terms of a distal outcome, e.g., Week 16 substance use) may concern either their main effects, averaging over JITAI options (e.g., Table 4 , B1 and B2), or their interactions with JITAI options (e.g., Table 4 , B3 and B4). The selected outcomes should measure changes at timescales (e.g., triannually or daily, respectively) that are suitable given the ADI and JITAI decision points (monthly or daily, respectively).

Sometimes multiple questions may be identified, perhaps too many to answer in a single study. In this case, a useful strategy might be to rank-order the questions in terms of both their scientific impact and novelty. On the basis of these scientific questions, investigators should formulate a single, simple, and clear main hypothesis accompanied by a limited number of secondary hypotheses and exploratory propositions.

Step 3: plan random assignments

The timing of random assignments and assignment probabilities should be guided by the scientific questions of interest while also addressing practical considerations. For example, if the JITAI under investigation is designed to address conditions that change every few hours (rather than every day), then random assignments to JITAI options should occur every few hours (e.g., Nahum-Shani, Potter, et al., 2021 ). If, because of considerations relating to burden or risk for habituation, individuals should not receive more than a certain number of JITAI options over a certain period of time (e.g., no more than two messages per day), then higher random-assignment probabilities can be assigned to JITAI options that are less burdensome and/or that can mitigate habituation (e.g., higher probability to not delivering relative to delivering a message; see discussion in Qian et al., 2022 ). If the ADI under investigation includes a dynamic tailoring variable (i.e., repeated assessments of response status used to transition individuals to a more intense intervention as soon as they show early signs of nonresponse), then the HED should again randomly assign nonresponders to subsequent ADI options at different time points (rather than at a single point in time, such as week 4 in Fig. 6 ) depending on when they show early signs of nonresponse (see example in Patrick et al., 2021 ).

Note that the example in Figure 6 involves random-assignment probabilities that are constant. However, certain scientific questions and practical considerations would require changing the random-assignment probabilities systematically during the trial. For example, consider the following scientific question: For nonresponders at Week 4, is it better (in terms of Week 16 substance use) to add coaching or to enhance the intensity of message delivery, averaging over JITAI options? This question can be answered by designing a HED in which nonresponders at Week 4 get randomly assigned again to two subsequent ADI options: (a) add coaching or (b) enhance the probability of delivering a message (vs. no message) in subsequent microrandom assignments (e.g., from 0.5 to 0.7). Furthermore, suppose that the goal is to investigate whether it is more beneficial (in terms of next-day number of drinks) to deliver a message when the individual experiences high risk versus low risk, averaging over ADI options. To ensure that there are adequate numbers of messages delivered both at high-risk times (which may be relatively rare) and at low-risk times, the HED can be designed to use a higher random-assignment probability to delivering (vs. not delivering) a message when individuals are classified as high risk and a lower probability when they are classified as low risk. In this example, different random-assignment probabilities to JITAI options are used for different individuals at different time points depending on a time-varying variable (see detailed discussion in Dempsey et al., 2020 ).

Furthermore, any conditions that restrict the random assignments (i.e., determine whether an individual should get randomly assigned to specific intervention options) must be specified on the basis of scientific questions and substantive knowledge. For example, if at any time it is inappropriate to deliver JITAI options (e.g., a message) because of scientific, ethical, feasibility, or burden considerations, then random assignments to JITAI options should be restricted only to those conditions in which their delivery is appropriate (e.g., micro-random assignment of an individual to JITAI options only when not driving a car: Battalio et al., 2021 ; or only if the individual completed a specific task such as self-monitoring: Nahum-Shani, Rabbi, et al., 2021 ). Similar considerations should be used when selecting tailoring variables such as response status to restrict the random assignments to subsequent ADI options.

In the current example ( Fig. 6 ), random assignments to stepping up to a more intense intervention at Week 4 is restricted to nonresponders only. This ADI option is not considered for responders to avoid delivering unnecessary treatment to individuals who are responsive to the initial intervention. In fact, because this motivating example did not include scientific questions about responders, this subgroup is not randomly assigned to any subsequent ADI options at Week 4 and instead continues with the initial intervention. If there are scientific questions about subsequent ADI options for responders (e.g., whether it is better to continue or step down the intensity of the initial intervention), then the HED could involve randomly assigning responders again as well as nonresponders at the second stage. In this case, both responders and nonresponders will be randomly assigned again, but the random assignment will be restricted to different subsequent ADI options (see an example in Nahum-Shani et al., 2017 ).

Recommended reading to support this step includes literature that provides guidelines for planning the random assignments in SMARTs (e.g., Nahum-Shani & Almirall, 2019 ; Nahum-Shani et al., 2012a ) and MRTs (e.g., Qian et al., 2022 ; Walton et al., 2018 ) in relation to motivating scientific questions and substantive knowledge about building ADIs and JITAIs, respectively.

Step 4: plan sample size

Similar to other experiments, the required sample size for a HED is typically affected by the effect size, the chosen Type I error rate, and the chosen statistical power. At this point, work to develop closed-form formulas for planning sample size for HEDs is still ongoing. However, we developed a simulation-based approach to plan sample size. An annotated code for implementing this approach is available online at https://github.com/dziakj1/Hybrid_Designs_Simulation . A brief user guide for applying this code is provided in Appendix C in the Supplemental Material .

Step 5: develop software for random assignment and delivery of digital-intervention components

Recall that the rapid random assignments in the HED are motivated to empirically inform the delivery of JITAI components that address conditions that change rapidly in the person’s natural environment. Hence, these options are typically delivered via mobile devices (e.g., smartphones, wearables) that can facilitate timely delivery of interventions in daily life. Because the type of technology used to deliver the interventions would have implications on the type of data that can be collected, researchers should work closely with software developers to ensure appropriate implementation and data collection. Recommended reading includes literature that provides guidelines for data collection and management in MRTs (e.g., Seewald et al., 2019 ). Careful attention should also be given to beta testing study procedures to ensure they operate as needed. This can be especially useful in anticipating and mitigating the various scenarios that can result in missing data before the study begins.

Other considerations

As with other studies, a detailed study protocol and manual of operations should be developed for the HED, including procedures to ensure and measure fidelity of implementation. The HED should be registered in an open-science framework before the conduct of the trial. We recommend specifying the planned analyses in the preregistration, including the list of control variables for inclusion in the models. Appendix A in the Supplemental Material provides example models that can be used to analyze the data, and Appendix D in the Supplemental Material provides annotated code to implement the analyses.

This article introduces HEDs, new experimental designs that can aid in the development of psychological interventions that integrate components that are adapted at multiple timescales. We describe some of the questions that HEDs can address and practical steps to guide the design of these trials. Although effectively integrating human-delivered and digital-intervention components is a key motivation for this design, the main difference between the HED and other experimental approaches is the multiple timescales at which study participants can be randomly assigned during the course of the trial. Hence, this design can potentially be used to inform the development of interventions that are not necessarily multimodality but nonetheless involve adaptation at multiple timescales (e.g., a fully digital intervention with multiple components that adapt to slow and fast changing conditions). For simplicity, this article focuses on one type of HED that integrates a prototypical SMART with a relatively simple MRT. However, HEDs can take on various forms depending on the scientific questions motivating the investigation. Additional research is needed to develop methods for analyzing data from different forms of HEDs and to find more convenient methods for planning sample size to address various types of scientific questions.

• Supplementary Material

Funded by the National Institutes of Health, Grants U01 CA229437, P50 DA054039, R01 DA039901, and R01 AA026574.

Declaration of Conflicting Interests

The author(s) declare that there were no conflicts of interest with respect to the authorship or the publication of this article.

Open Practices

Open Data: not applicable

Open Materials: https://github.com/dziakj1/Hybrid_Designs_Simulation/tree/Final_Submitted_Version_To_AMPPS_2022

Preregistration: not applicable

All materials have been made publicly available via GitHub and can be accessed at https://github.com/dziakj1/Hybrid_Designs_Simulation/tree/Final_Submitted_Version_To_AMPPS_2022 . This article has received the badge for Open Materials. More information about the Open Practices badges can be found at http://www.psychologicalscience.org/publications/badges .

Supplemental Material

Additional supporting information can be found at http://journals.sagepub.com/doi/suppl/10.1177/25152459221114279

• Battalio SL, Conroy DE, Dempsey W, Liao P, Menictas M, Murphy S, Nahum-Shani I, Qian T, Kumar S, & Spring B (2021). Sense2Stop: A micro-randomized trial using wearable sensors to optimize a just-in-time-adaptive stress management intervention for smoking relapse prevention . Contemporary Clinical Trials , 109 , Article 106534. 10.1016/j.cct.2021.106534 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Belzer ME, MacDonell KK, Ghosh S, Naar S, McAvoy-Banerjea J, Gurung S, Cain D, Fan CA, & Parsons JT (2018). Adaptive antiretroviral therapy adherence interventions for youth living with HIV through text message and cell phone support with and without incentives: Protocol for a sequential multiple assignment randomized trial (SMART) . JMIR Research Protocols , 7 ( 12 ), Article 11183. 10.2196/11183 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Bernstein SL, Carter PM, Meurer W, Walton MA, Kidwell KM, Cunningham RM, Dziura J, & Collins LM (2022). Advances in clinical trials methodology: Intervention optimization approaches in emergency medicine . The American Journal of Emergency Medicine , 53 , 6–11. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Chow JC, & Hampton LH (2022). A systematic review of sequential multiple-assignment randomized trials in educational research . Educational Psychology Review . Advance online publication. 10.1007/s10648-022-09660-x [ CrossRef ] [ Google Scholar ]
• Collins LM (2018). Optimization of behavioral, biobehavioral, and biomedical interventions: The multiphase optimization strategy (MOST) . Springer. [ Google Scholar ]
• Collins LM, Murphy SA, & Bierman KL (2004). A conceptual framework for adaptive preventive interventions . Prevention Science , 5 ( 3 ), 185–196. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Collins LM, Nahum-Shani I, & Almirall D (2014). Optimization of behavioral dynamic treatment regimens based on the sequential, multiple assignment, randomized trial (SMART) . Clinical Trials , 11 ( 4 ), 426–434. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Comer JS, Conroy K, & Timmons AC (2019). Ensuring wearable devices don’t wear out their welcome: Cautions for the mental health care road ahead . Clinical Psychology: Science and Practice , 26 ( 3 ), Article 12297. 10.1111/cpsp.12297 [ CrossRef ] [ Google Scholar ]
• Conroy DE, West AB, Brunke-Reese D, Thomaz E, & Streeper NM (2020). Just-in-time adaptive intervention to promote fluid consumption in patients with kidney stones . Health Psychology , 39 ( 12 ), 1062–1069. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Cook CR, Kilgus SP, & Burns MK (2018). Advancing the science and practice of precision education to enhance student outcomes . Journal of School Psychology , 66 , 4–10. [ Abstract ] [ Google Scholar ]
• Coppersmith G (2022). Digital life data in the clinical whitespace . Current Directions in Psychological Science , 31 ( 1 ), 34–40. 10.1177/09637214211068839 [ CrossRef ] [ Google Scholar ]
• Coughlin LN, Nahum-Shani I, Philyaw-Kotov ML, Bonar EE, Rabbi M, Klasnja P, Murphy S, & Walton MA (2021). Developing an adaptive mobile intervention to address risky substance use among adolescents and emerging adults: Usability study . JMIR mHealth and uHealth , 9 ( 1 ), Article e24424. 10.2196/24424 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Czajkowski SM, & Hunter CM (2021). From ideas to interventions: A review and comparison of frameworks used in early phase behavioral translation research . Health Psychology , 40 ( 12 ), 829–844. [ Abstract ] [ Google Scholar ]
• Czyz EK, King CA, Prouty D, Micol VJ, Walton M, & Nahum-Shani I (2021). Adaptive intervention for prevention of adolescent suicidal behavior after hospitalization: A pilot sequential multiple assignment randomized trial . Journal of Child Psychology and Psychiatry , 62 ( 8 ), 1019–1031. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Dempsey W, Liao P, Kumar S, & Murphy SA (2020). The stratified micro-randomized trial design: Sample size considerations for testing nested causal effects of time-varying treatments . The Annals of Applied Statistics , 14 ( 2 ), 661–648. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Eden D (2017). Field experiments in organizations . Annual Review of Organizational Psychology and Organizational Behavior , 4 , 91–122. [ Google Scholar ]
• Figueroa CA, Deliu N, Chakraborty B, Modiri A, Xu J, Aggarwal J, Jay Williams J, Lyles C, & Aguilera A (2021). Daily motivational text messages to promote physical activity in university students: Results from a micro-randomized trial . Annals of Behavioral Medicine , 56 ( 2 ), 212–218. 10.1093/abm/kaab028 [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Ghosh P, Nahum-Shani I, Spring B, & Chakraborty B (2020). Noninferiority and equivalence tests in sequential, multiple assignment, randomized trials (SMARTs) . Psychological Methods , 25 ( 2 ), 182–205. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Goldstein SP, Evans BC, Flack D, Juarascio A, Manasse S, Zhang F, & Forman EM (2017). Return of the JITAI: Applying a just-in-time adaptive intervention framework to the development of m-health solutions for addictive behaviors . International Journal of Behavioral Medicine , 24 ( 5 ), 673–682. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Howard MC, & Jacobs RR (2016). The multiphase optimization strategy (MOST) and the sequential multiple assignment randomized trial (SMART): Two novel evaluation methods for developing optimal training programs . Journal of Organizational Behavior , 37 ( 8 ), 1246–1270. [ Google Scholar ]
• Huh J, Cerrada CJ, Dzubur E, Dunton GF, Spruijt-Metz D, & Leventhal AM (2020). Effect of a mobile just-in-time implementation intention intervention on momentary smoking lapses in smoking cessation attempts among Asian American young adults . Translational Behavioral Medicine , 11 ( 1 ), 216–225. 10.1093/tbm/ibz183 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Kitayama S (2021, February 26). Innovative methods and scientific process . Observer. https://www.psychologicalscience.org/observer/innovative-methods [ Google Scholar ]
• Koch ED, Moukhtarian TR, Skirrow C, Bozhilova N, Asherson P, & Ebner-Priemer UW (2021). Using e-diaries to investigate ADHD–state-of-the-art and the promising feature of just-in-time-adaptive interventions . Neuroscience & Biobehavioral Reviews , 127 , 884–898. [ Abstract ] [ Google Scholar ]
• Lattie EG, Stiles-Shields C, & Graham AK (2022). An overview of and recommendations for more accessible digital mental health services . Nature Reviews Psychology , 1 ( 2 ), 87–100. 10.1038/s44159-021-00003-1 [ CrossRef ] [ Google Scholar ]
• Lavori PW, & Dawson R (2000). A design for testing clinical strategies: Biased adaptive within-subject randomization . Journal of the Royal Statistical Society A: Statistics in Society , 163 ( 1 ), 29–38. [ Google Scholar ]
• Majeika CE, Bruhn AL, Sterrett BI, & McDaniel S (2020). Reengineering Tier 2 interventions for responsive decision making: An adaptive intervention process . Journal of Applied School Psychology , 36 ( 2 ), 111–132. [ Google Scholar ]
• Marlowe DB, Festinger DS, Dugosh KL, Benasutti KM, Fox G, & Croft JR (2012). Adaptive programming improves outcomes in drug court: An experimental trial . Criminal Justice and Behavior , 39 ( 4 ), 514–532. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Mohr D, Cuijpers P, & Lehman K (2011). Supportive accountability: A model for providing human support to enhance adherence to eHealth interventions . Journal of Medical Internet Research , 13 ( 1 ), Article e30. 10.2196/jmir.1602 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Murphy SA (2005). An experimental design for the development of adaptive treatment strategies . Statistics in Medicine , 24 ( 10 ), 1455–1481. [ Abstract ] [ Google Scholar ]
• Murphy SA, Lynch KG, Oslin D, McKay JR, & TenHave T (2007). Developing adaptive treatment strategies in substance abuse research . Drug and Alcohol Dependence , 88 , S24–S30. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Murphy SA, & McKay JR (2004). Adaptive treatment strategies: An emerging approach for improving treatment effectiveness . Clinical Science , 12 , 7–13. [ Google Scholar ]
• Nahum-Shani I, & Almirall D (2019). An introduction to adaptive interventions and SMART designs in education (NCSER 2020–001) . National Center for Special Education Research. [ Google Scholar ]
• Nahum-Shani I, Almirall D, Yap JR, McKay JR, Lynch KG, Freiheit EA, & Dziak JJ (2020). SMART longitudinal analysis: A tutorial for using repeated outcome measures from SMART studies to compare adaptive interventions . Psychological Methods , 25 ( 1 ), 1–29. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Nahum-Shani I, Dziak JJ, & Wetter DW (2022). MCMTC: A pragmatic framework for selecting an experimental design to inform the development of digital interventions . Frontiers in Digital Health , 4 , Article 798025. 10.3389/fdgth.2022.798025 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Nahum-Shani I, Ertefaie A, Lu X, Lynch KG, McKay JR, Oslin DW, & Almirall D (2017). A SMART data analysis method for constructing adaptive treatment strategies for substance use disorders . Addiction , 112 ( 5 ), 901–909. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Nahum-Shani I, Hekler E, & Spruijt-Metz D (2015). Building health behavior models to guide the development of just-in-time adaptive interventions: A pragmatic framework . Health Psychology , 34 ( Suppl. ), 1209–1219. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Nahum-Shani I, Potter LN, Lam CY, Yap J, Moreno A, Stoffel R, Wu Z, Wan N, Dempsey W, & Kumar S (2021). The mobile assistance for regulating smoking (MARS) micro-randomized trial design protocol . Contemporary Clinical Trials , 110 , Article 106513. 10.1016/j.cct.2021.106513 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano GA, Waxmonsky JG, Yu J, & Murphy SA (2012a). Experimental design and primary data analysis methods for comparing adaptive interventions . Psychological Methods , 17 ( 4 ), 457–477. 10.1037/a0029372 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Nahum-Shani I, Qian M, Almirall D, Pelham WE, Gnagy B, Fabiano GA, Waxmonsky JG, Yu J, & Murphy SA (2012b). Q-learning: A data analysis method for constructing adaptive interventions . Psychological Methods , 17 ( 4 ), 478–494. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Nahum-Shani I, Rabbi M, Yap J, Philyaw-Kotov ML, Klasnja P, Bonar EE, Cunningham RM, Murphy SA, & Walton MA (2021). Translating strategies for promoting engagement in mobile health: A proof-of-concept microrandomized trial . Health Psychology , 40 ( 12 ), 974–987. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Nahum-Shani I, Shaw SD, Carpenter SM, Murphy SA, & Yoon C (2022). Engagement in digital interventions . American Psychologist . Advance online publication. 10.1037/amp0000983 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Nahum-Shani I, Smith SN, Spring BJ, Collins LM, Witkiewitz K, Tewari A, & Murphy SA (2018). Just-in-time adaptive interventions (JITAIs) in mobile health: Key components and design principles for ongoing health behavior support . Annals of Behavioral Medicine , 52 ( 6 ), 446–462. 10.1007/s12160-016-9830-8 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Patrick ME, Lyden GR, Morrell N, Mehus CJ, Gunlicks-Stoessel M, Lee CM, King CA, Bonar EE, Nahum-Shani I, & Almirall D (2021). Main outcomes of M-bridge: A sequential multiple assignment randomized trial (SMART) for developing an adaptive preventive intervention for college drinking . Journal of Consulting and Clinical Psychology , 89 ( 7 ), 601–614. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Pelham WE Jr., Fabiano GA, Waxmonsky JG, Greiner AR, Gnagy EM, Pelham WE III, Coxe S, Verley J, Bhatia I, & Hart K (2016). Treatment sequencing for childhood ADHD: A multiple-randomization study of adaptive medication and behavioral interventions . Journal of Clinical Child & Adolescent Psychology , 45 ( 4 ), 396–415. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Qian T, Walton AE, Collins LM, Klasnja P, Lanza ST, Nahum-Shani I, Rabbi M, Russell MA, Walton MA, & Yoo H (2022). The microrandomized trial for developing digital interventions: Experimental design and data analysis considerations . Psychological Methods . Advance online publication. 10.1037/met0000283 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]
• Ritterband LM, Thorndike FP, Cox DJ, Kovatchev BP, & Gonder-Frederick LA (2009). A behavior change model for internet interventions . Annals of Behavioral Medicine , 38 ( 1 ), 18–27. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Roberts G, Clemens N, Doabler CT, Vaughn S, Almirall D, & Nahum-Shani I (2021). Multitiered systems of support, adaptive interventions, and SMART designs . Exceptional Children , 88 ( 1 ), 8–25. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Schueller SM, Tomasino KN, & Mohr DC (2017). Integrating human support into behavioral intervention technologies: The efficiency model of support . Clinical Psychology: Science and Practice , 24 ( 1 ), 27–45. [ Google Scholar ]
• Seewald NJ, Smith SN, Lee AJ, Klasnja P, & Murphy SA (2019). Practical considerations for data collection and management in mobile health micro-randomized trials . Statistics in Biosciences , 11 ( 2 ), 355–370. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Spring B (2019). Sound health care economics: Provide the treatment needed (not less, not more) . Health Psychology , 38 ( 8 ), 701–704. [ Abstract ] [ Google Scholar ]
• Valle CG, Nezami BT, & Tate DF (2020). Designing in-app messages to nudge behavior change: Lessons learned from a weight management app for young adults . Organizational Behavior and Human Decision Processes , 161 , 95–101. [ Google Scholar ]
• Walton A, Nahum-Shani I, Crosby L, Klasnja P, & Murphy S (2018). Optimizing digital integrated care via micro-randomized trials . Clinical Pharmacology & Therapeutics , 104 ( 1 ), 53–58. [ Europe PMC free article ] [ Abstract ] [ Google Scholar ]
• Wentzel J, van der Vaart R, Bohlmeijer ET, & van Gemert-Pijnen JE (2016). Mixing online and face-to-face therapy: How to benefit from blended care in mental health care . JMIR Mental Health , 3 ( 1 ), Article e9. 10.2196/mental.4534 [ Europe PMC free article ] [ Abstract ] [ CrossRef ] [ Google Scholar ]

Full text links 

Read article at publisher's site: https://doi.org/10.1177/25152459221114279

Citations & impact 

Impact metrics, citations of article over time, alternative metrics.

Article citations

Intervention optimization: a paradigm shift and its potential implications for clinical psychology..

Collins LM , Nahum-Shani I , Guastaferro K , Strayhorn JC , Vanness DJ , Murphy SA

Annu Rev Clin Psychol , 20(1):21-47, 02 Jul 2024

Cited by: 1 article | PMID: 38316143

Latent transition analysis of time-varying cannabis use motives to inform adaptive interventions.

West BT , Ma Y , Lankenau S , Wong CF , Bonar EE , Patrick ME , Walton MA , McCabe SE

Psychol Addict Behav , 38(7):759-771, 23 May 2024

Cited by: 0 articles | PMID: 38780582

Optimizing an adaptive digital oral health intervention for promoting oral self-care behaviors: Micro-randomized trial protocol.

Nahum-Shani I , Greer ZM , Trella AL , Zhang KW , Carpenter SM , Rünger D , Elashoff D , Murphy SA , Shetty V

Contemp Clin Trials , 139:107464, 01 Feb 2024

Cited by: 0 articles | PMID: 38307224

Digital Adaptive Behavioral Interventions to Improve HIV Prevention and Care: Innovations in Intervention Approach and Experimental Design.

Nahum-Shani I , Naar S

Curr HIV/AIDS Rep , 20(6):502-512, 04 Nov 2023

Cited by: 0 articles | PMID: 37924458

Editorial: Digital technology for tobacco control: Novel data collection, study designs, and interventions.

Potter LN , Nahum-Shani I , Wetter DW

Front Digit Health , 5:1341759, 01 Dec 2023

Cited by: 0 articles | PMID: 38107825 | PMCID: PMC10725255

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Design of experiments with sequential randomizations on multiple timescales: the hybrid experimental design.

Nahum-Shani I , Dziak JJ , Venera H , Pfammatter AF , Spring B , Dempsey W

Behav Res Methods , 56(3):1770-1792, 08 May 2023

Cited by: 5 articles | PMID: 37156958 | PMCID: PMC10961682

Free full text in Europe PMC

Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas.

Crider K , Williams J , Qi YP , Gutman J , Yeung L , Mai C , Finkelstain J , Mehta S , Pons-Duran C , Menéndez C , Moraleda C , Rogers L , Daniels K , Green P

Cochrane Database Syst Rev , 2(2022), 01 Feb 2022

Cited by: 12 articles | PMID: 36321557 | PMCID: PMC8805585

Review Free full text in Europe PMC

MCMTC: A Pragmatic Framework for Selecting an Experimental Design to Inform the Development of Digital Interventions.

Nahum-Shani I , Dziak JJ , Wetter DW

Front Digit Health , 4:798025, 09 Mar 2022

Cited by: 9 articles | PMID: 35355685 | PMCID: PMC8959436

Funding 

Funders who supported this work.

NCI NIH HHS (1)

Grant ID: U01 CA229437

64 publication s

NIAAA NIH HHS (1)

Grant ID: R01 AA026574

13 publication s

NIDA NIH HHS (2)

Grant ID: P50 DA054039

78 publication s

Grant ID: R01 DA039901

129 publication s

national institutes of health (1)

Grant ID: U01 CA229437, P50 DA054039, R01 DA039901, and R01 AA026574

1 publication

Partnerships & funding

Europe PMC is developed by EMBL-EBI with support from the Europe PMC Funders' Group , in collaboration with the National Library of Medicine (NLM) , as part of the PubMed Central International archive network.

Europe PMC is an ELIXIR Core Data Resource , Global Core Biodata Resource , and conforms with EMBL-EBI’s long term data preservation policies .

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

10 Experimental research

Experimental research—often considered to be the ‘gold standard’ in research designs—is one of the most rigorous of all research designs. In this design, one or more independent variables are manipulated by the researcher (as treatments), subjects are randomly assigned to different treatment levels (random assignment), and the results of the treatments on outcomes (dependent variables) are observed. The unique strength of experimental research is its internal validity (causality) due to its ability to link cause and effect through treatment manipulation, while controlling for the spurious effect of extraneous variable.

Experimental research is best suited for explanatory research—rather than for descriptive or exploratory research—where the goal of the study is to examine cause-effect relationships. It also works well for research that involves a relatively limited and well-defined set of independent variables that can either be manipulated or controlled. Experimental research can be conducted in laboratory or field settings. Laboratory experiments , conducted in laboratory (artificial) settings, tend to be high in internal validity, but this comes at the cost of low external validity (generalisability), because the artificial (laboratory) setting in which the study is conducted may not reflect the real world. Field experiments are conducted in field settings such as in a real organisation, and are high in both internal and external validity. But such experiments are relatively rare, because of the difficulties associated with manipulating treatments and controlling for extraneous effects in a field setting.

Experimental research can be grouped into two broad categories: true experimental designs and quasi-experimental designs. Both designs require treatment manipulation, but while true experiments also require random assignment, quasi-experiments do not. Sometimes, we also refer to non-experimental research, which is not really a research design, but an all-inclusive term that includes all types of research that do not employ treatment manipulation or random assignment, such as survey research, observational research, and correlational studies.

Basic concepts

Treatment and control groups. In experimental research, some subjects are administered one or more experimental stimulus called a treatment (the treatment group ) while other subjects are not given such a stimulus (the control group ). The treatment may be considered successful if subjects in the treatment group rate more favourably on outcome variables than control group subjects. Multiple levels of experimental stimulus may be administered, in which case, there may be more than one treatment group. For example, in order to test the effects of a new drug intended to treat a certain medical condition like dementia, if a sample of dementia patients is randomly divided into three groups, with the first group receiving a high dosage of the drug, the second group receiving a low dosage, and the third group receiving a placebo such as a sugar pill (control group), then the first two groups are experimental groups and the third group is a control group. After administering the drug for a period of time, if the condition of the experimental group subjects improved significantly more than the control group subjects, we can say that the drug is effective. We can also compare the conditions of the high and low dosage experimental groups to determine if the high dose is more effective than the low dose.

Treatment manipulation. Treatments are the unique feature of experimental research that sets this design apart from all other research methods. Treatment manipulation helps control for the ‘cause’ in cause-effect relationships. Naturally, the validity of experimental research depends on how well the treatment was manipulated. Treatment manipulation must be checked using pretests and pilot tests prior to the experimental study. Any measurements conducted before the treatment is administered are called pretest measures , while those conducted after the treatment are posttest measures .

Random selection and assignment. Random selection is the process of randomly drawing a sample from a population or a sampling frame. This approach is typically employed in survey research, and ensures that each unit in the population has a positive chance of being selected into the sample. Random assignment, however, is a process of randomly assigning subjects to experimental or control groups. This is a standard practice in true experimental research to ensure that treatment groups are similar (equivalent) to each other and to the control group prior to treatment administration. Random selection is related to sampling, and is therefore more closely related to the external validity (generalisability) of findings. However, random assignment is related to design, and is therefore most related to internal validity. It is possible to have both random selection and random assignment in well-designed experimental research, but quasi-experimental research involves neither random selection nor random assignment.

Threats to internal validity. Although experimental designs are considered more rigorous than other research methods in terms of the internal validity of their inferences (by virtue of their ability to control causes through treatment manipulation), they are not immune to internal validity threats. Some of these threats to internal validity are described below, within the context of a study of the impact of a special remedial math tutoring program for improving the math abilities of high school students.

History threat is the possibility that the observed effects (dependent variables) are caused by extraneous or historical events rather than by the experimental treatment. For instance, students’ post-remedial math score improvement may have been caused by their preparation for a math exam at their school, rather than the remedial math program.

Maturation threat refers to the possibility that observed effects are caused by natural maturation of subjects (e.g., a general improvement in their intellectual ability to understand complex concepts) rather than the experimental treatment.

Testing threat is a threat in pre-post designs where subjects’ posttest responses are conditioned by their pretest responses. For instance, if students remember their answers from the pretest evaluation, they may tend to repeat them in the posttest exam.

Not conducting a pretest can help avoid this threat.

Instrumentation threat , which also occurs in pre-post designs, refers to the possibility that the difference between pretest and posttest scores is not due to the remedial math program, but due to changes in the administered test, such as the posttest having a higher or lower degree of difficulty than the pretest.

Mortality threat refers to the possibility that subjects may be dropping out of the study at differential rates between the treatment and control groups due to a systematic reason, such that the dropouts were mostly students who scored low on the pretest. If the low-performing students drop out, the results of the posttest will be artificially inflated by the preponderance of high-performing students.

Regression threat —also called a regression to the mean—refers to the statistical tendency of a group’s overall performance to regress toward the mean during a posttest rather than in the anticipated direction. For instance, if subjects scored high on a pretest, they will have a tendency to score lower on the posttest (closer to the mean) because their high scores (away from the mean) during the pretest were possibly a statistical aberration. This problem tends to be more prevalent in non-random samples and when the two measures are imperfectly correlated.

Two-group experimental designs

Pretest-posttest control group design . In this design, subjects are randomly assigned to treatment and control groups, subjected to an initial (pretest) measurement of the dependent variables of interest, the treatment group is administered a treatment (representing the independent variable of interest), and the dependent variables measured again (posttest). The notation of this design is shown in Figure 10.1.

Statistical analysis of this design involves a simple analysis of variance (ANOVA) between the treatment and control groups. The pretest-posttest design handles several threats to internal validity, such as maturation, testing, and regression, since these threats can be expected to influence both treatment and control groups in a similar (random) manner. The selection threat is controlled via random assignment. However, additional threats to internal validity may exist. For instance, mortality can be a problem if there are differential dropout rates between the two groups, and the pretest measurement may bias the posttest measurement—especially if the pretest introduces unusual topics or content.

Posttest -only control group design . This design is a simpler version of the pretest-posttest design where pretest measurements are omitted. The design notation is shown in Figure 10.2.

The treatment effect is measured simply as the difference in the posttest scores between the two groups:

The appropriate statistical analysis of this design is also a two-group analysis of variance (ANOVA). The simplicity of this design makes it more attractive than the pretest-posttest design in terms of internal validity. This design controls for maturation, testing, regression, selection, and pretest-posttest interaction, though the mortality threat may continue to exist.

Because the pretest measure is not a measurement of the dependent variable, but rather a covariate, the treatment effect is measured as the difference in the posttest scores between the treatment and control groups as:

Due to the presence of covariates, the right statistical analysis of this design is a two-group analysis of covariance (ANCOVA). This design has all the advantages of posttest-only design, but with internal validity due to the controlling of covariates. Covariance designs can also be extended to pretest-posttest control group design.

Factorial designs

Two-group designs are inadequate if your research requires manipulation of two or more independent variables (treatments). In such cases, you would need four or higher-group designs. Such designs, quite popular in experimental research, are commonly called factorial designs. Each independent variable in this design is called a factor , and each subdivision of a factor is called a level . Factorial designs enable the researcher to examine not only the individual effect of each treatment on the dependent variables (called main effects), but also their joint effect (called interaction effects).

In a factorial design, a main effect is said to exist if the dependent variable shows a significant difference between multiple levels of one factor, at all levels of other factors. No change in the dependent variable across factor levels is the null case (baseline), from which main effects are evaluated. In the above example, you may see a main effect of instructional type, instructional time, or both on learning outcomes. An interaction effect exists when the effect of differences in one factor depends upon the level of a second factor. In our example, if the effect of instructional type on learning outcomes is greater for three hours/week of instructional time than for one and a half hours/week, then we can say that there is an interaction effect between instructional type and instructional time on learning outcomes. Note that the presence of interaction effects dominate and make main effects irrelevant, and it is not meaningful to interpret main effects if interaction effects are significant.

Hybrid experimental designs

Hybrid designs are those that are formed by combining features of more established designs. Three such hybrid designs are randomised bocks design, Solomon four-group design, and switched replications design.

Randomised block design. This is a variation of the posttest-only or pretest-posttest control group design where the subject population can be grouped into relatively homogeneous subgroups (called blocks ) within which the experiment is replicated. For instance, if you want to replicate the same posttest-only design among university students and full-time working professionals (two homogeneous blocks), subjects in both blocks are randomly split between the treatment group (receiving the same treatment) and the control group (see Figure 10.5). The purpose of this design is to reduce the ‘noise’ or variance in data that may be attributable to differences between the blocks so that the actual effect of interest can be detected more accurately.

Solomon four-group design . In this design, the sample is divided into two treatment groups and two control groups. One treatment group and one control group receive the pretest, and the other two groups do not. This design represents a combination of posttest-only and pretest-posttest control group design, and is intended to test for the potential biasing effect of pretest measurement on posttest measures that tends to occur in pretest-posttest designs, but not in posttest-only designs. The design notation is shown in Figure 10.6.

Switched replication design . This is a two-group design implemented in two phases with three waves of measurement. The treatment group in the first phase serves as the control group in the second phase, and the control group in the first phase becomes the treatment group in the second phase, as illustrated in Figure 10.7. In other words, the original design is repeated or replicated temporally with treatment/control roles switched between the two groups. By the end of the study, all participants will have received the treatment either during the first or the second phase. This design is most feasible in organisational contexts where organisational programs (e.g., employee training) are implemented in a phased manner or are repeated at regular intervals.

Quasi-experimental designs

Quasi-experimental designs are almost identical to true experimental designs, but lacking one key ingredient: random assignment. For instance, one entire class section or one organisation is used as the treatment group, while another section of the same class or a different organisation in the same industry is used as the control group. This lack of random assignment potentially results in groups that are non-equivalent, such as one group possessing greater mastery of certain content than the other group, say by virtue of having a better teacher in a previous semester, which introduces the possibility of selection bias . Quasi-experimental designs are therefore inferior to true experimental designs in interval validity due to the presence of a variety of selection related threats such as selection-maturation threat (the treatment and control groups maturing at different rates), selection-history threat (the treatment and control groups being differentially impacted by extraneous or historical events), selection-regression threat (the treatment and control groups regressing toward the mean between pretest and posttest at different rates), selection-instrumentation threat (the treatment and control groups responding differently to the measurement), selection-testing (the treatment and control groups responding differently to the pretest), and selection-mortality (the treatment and control groups demonstrating differential dropout rates). Given these selection threats, it is generally preferable to avoid quasi-experimental designs to the greatest extent possible.

In addition, there are quite a few unique non-equivalent designs without corresponding true experimental design cousins. Some of the more useful of these designs are discussed next.

Regression discontinuity (RD) design . This is a non-equivalent pretest-posttest design where subjects are assigned to the treatment or control group based on a cut-off score on a preprogram measure. For instance, patients who are severely ill may be assigned to a treatment group to test the efficacy of a new drug or treatment protocol and those who are mildly ill are assigned to the control group. In another example, students who are lagging behind on standardised test scores may be selected for a remedial curriculum program intended to improve their performance, while those who score high on such tests are not selected from the remedial program.

Because of the use of a cut-off score, it is possible that the observed results may be a function of the cut-off score rather than the treatment, which introduces a new threat to internal validity. However, using the cut-off score also ensures that limited or costly resources are distributed to people who need them the most, rather than randomly across a population, while simultaneously allowing a quasi-experimental treatment. The control group scores in the RD design do not serve as a benchmark for comparing treatment group scores, given the systematic non-equivalence between the two groups. Rather, if there is no discontinuity between pretest and posttest scores in the control group, but such a discontinuity persists in the treatment group, then this discontinuity is viewed as evidence of the treatment effect.

Proxy pretest design . This design, shown in Figure 10.11, looks very similar to the standard NEGD (pretest-posttest) design, with one critical difference: the pretest score is collected after the treatment is administered. A typical application of this design is when a researcher is brought in to test the efficacy of a program (e.g., an educational program) after the program has already started and pretest data is not available. Under such circumstances, the best option for the researcher is often to use a different prerecorded measure, such as students’ grade point average before the start of the program, as a proxy for pretest data. A variation of the proxy pretest design is to use subjects’ posttest recollection of pretest data, which may be subject to recall bias, but nevertheless may provide a measure of perceived gain or change in the dependent variable.

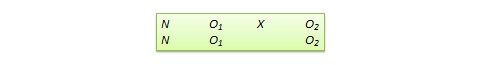
Separate pretest-posttest samples design . This design is useful if it is not possible to collect pretest and posttest data from the same subjects for some reason. As shown in Figure 10.12, there are four groups in this design, but two groups come from a single non-equivalent group, while the other two groups come from a different non-equivalent group. For instance, say you want to test customer satisfaction with a new online service that is implemented in one city but not in another. In this case, customers in the first city serve as the treatment group and those in the second city constitute the control group. If it is not possible to obtain pretest and posttest measures from the same customers, you can measure customer satisfaction at one point in time, implement the new service program, and measure customer satisfaction (with a different set of customers) after the program is implemented. Customer satisfaction is also measured in the control group at the same times as in the treatment group, but without the new program implementation. The design is not particularly strong, because you cannot examine the changes in any specific customer’s satisfaction score before and after the implementation, but you can only examine average customer satisfaction scores. Despite the lower internal validity, this design may still be a useful way of collecting quasi-experimental data when pretest and posttest data is not available from the same subjects.

An interesting variation of the NEDV design is a pattern-matching NEDV design , which employs multiple outcome variables and a theory that explains how much each variable will be affected by the treatment. The researcher can then examine if the theoretical prediction is matched in actual observations. This pattern-matching technique—based on the degree of correspondence between theoretical and observed patterns—is a powerful way of alleviating internal validity concerns in the original NEDV design.

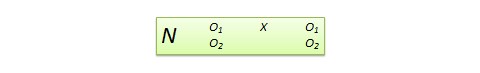
Perils of experimental research

Experimental research is one of the most difficult of research designs, and should not be taken lightly. This type of research is often best with a multitude of methodological problems. First, though experimental research requires theories for framing hypotheses for testing, much of current experimental research is atheoretical. Without theories, the hypotheses being tested tend to be ad hoc, possibly illogical, and meaningless. Second, many of the measurement instruments used in experimental research are not tested for reliability and validity, and are incomparable across studies. Consequently, results generated using such instruments are also incomparable. Third, often experimental research uses inappropriate research designs, such as irrelevant dependent variables, no interaction effects, no experimental controls, and non-equivalent stimulus across treatment groups. Findings from such studies tend to lack internal validity and are highly suspect. Fourth, the treatments (tasks) used in experimental research may be diverse, incomparable, and inconsistent across studies, and sometimes inappropriate for the subject population. For instance, undergraduate student subjects are often asked to pretend that they are marketing managers and asked to perform a complex budget allocation task in which they have no experience or expertise. The use of such inappropriate tasks, introduces new threats to internal validity (i.e., subject’s performance may be an artefact of the content or difficulty of the task setting), generates findings that are non-interpretable and meaningless, and makes integration of findings across studies impossible.

The design of proper experimental treatments is a very important task in experimental design, because the treatment is the raison d’etre of the experimental method, and must never be rushed or neglected. To design an adequate and appropriate task, researchers should use prevalidated tasks if available, conduct treatment manipulation checks to check for the adequacy of such tasks (by debriefing subjects after performing the assigned task), conduct pilot tests (repeatedly, if necessary), and if in doubt, use tasks that are simple and familiar for the respondent sample rather than tasks that are complex or unfamiliar.

In summary, this chapter introduced key concepts in the experimental design research method and introduced a variety of true experimental and quasi-experimental designs. Although these designs vary widely in internal validity, designs with less internal validity should not be overlooked and may sometimes be useful under specific circumstances and empirical contingencies.

Social Science Research: Principles, Methods and Practices (Revised edition) Copyright © 2019 by Anol Bhattacherjee is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Design of experiments with sequential randomizations on multiple timescales: the hybrid experimental design

Affiliations.

• 1 Institute for Social Research, University of Michigan, Ann Arbor, MI, USA. [email protected].
• 2 Institute for Health Research and Policy, University of Illinois Chicago, Chicago, IL, USA.
• 3 School of Public Health and Institute for Social Research, University of Michigan, Ann Arbor, MI, USA.
• 4 College of Education, Health, and Human Sciences, The University of Tennessee Knoxville, Knoxville, TN, USA.
• 5 Feinberg School of Medicine, Northwestern University, Evanston, IL, USA.
• PMID: 37156958
• PMCID: PMC10961682
• DOI: 10.3758/s13428-023-02119-z

Psychological interventions, especially those leveraging mobile and wireless technologies, often include multiple components that are delivered and adapted on multiple timescales (e.g., coaching sessions adapted monthly based on clinical progress, combined with motivational messages from a mobile device adapted daily based on the person's daily emotional state). The hybrid experimental design (HED) is a new experimental approach that enables researchers to answer scientific questions about the construction of psychological interventions in which components are delivered and adapted on different timescales. These designs involve sequential randomizations of study participants to intervention components, each at an appropriate timescale (e.g., monthly randomization to different intensities of coaching sessions and daily randomization to different forms of motivational messages). The goal of the current manuscript is twofold. The first is to highlight the flexibility of the HED by conceptualizing this experimental approach as a special form of a factorial design in which different factors are introduced at multiple timescales. We also discuss how the structure of the HED can vary depending on the scientific question(s) motivating the study. The second goal is to explain how data from various types of HEDs can be analyzed to answer a variety of scientific questions about the development of multicomponent psychological interventions. For illustration, we use a completed HED to inform the development of a technology-based weight loss intervention that integrates components that are delivered and adapted on multiple timescales.

Keywords: Digital interventions; Hybrid experimental designs (HED); Micro-randomized trial (MRT); Multimodal adaptive intervention (MADI); Sequential multiple assignment randomized trial (SMART); factorial experiments.

© 2023. The Psychonomic Society, Inc.

Publication types

• Research Support, N.I.H., Extramural
• Computers, Handheld
• Motivation*
• Random Allocation
• Research Design*

Grants and funding

• R01 DA039901/DA/NIDA NIH HHS/United States
• R01 DK125749/DK/NIDDK NIH HHS/United States
• R01 DK108678/DK/NIDDK NIH HHS/United States
• R01 DK134629/DK/NIDDK NIH HHS/United States
• U01 CA229437/CA/NCI NIH HHS/United States
• P50 DA054039/DA/NIDA NIH HHS/United States

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 11 November 2024

EvoAI enables extreme compression and reconstruction of the protein sequence space

• Ziyuan Ma 1   na1 ,
• Wenjie Li 1   na1 ,
• Yunhao Shen 1   na1 ,
• Yunxin Xu   ORCID: orcid.org/0000-0002-9981-2097 2   na1 ,
• Gengjiang Liu 1 ,
• Jiamin Chang 1 ,
• Zeju Li 1 ,
• Hong Qin 1 ,
• Boxue Tian   ORCID: orcid.org/0000-0002-5830-0669 1 , 3 ,
• Haipeng Gong   ORCID: orcid.org/0000-0002-5532-1640 2 ,
• David R. Liu   ORCID: orcid.org/0000-0002-9943-7557 4 , 5 , 6 ,
• B. W. Thuronyi   ORCID: orcid.org/0000-0003-0821-3791 7 ,
• Christopher A. Voigt   ORCID: orcid.org/0000-0003-0844-4776 8 &
• Shuyi Zhang   ORCID: orcid.org/0000-0001-8500-5836 1 , 3 , 9 , 10  

Nature Methods ( 2024 ) Cite this article

3 Altmetric

Metrics details

• Biological techniques
• Computational biology and bioinformatics
• Protein design
• Synthetic biology

Designing proteins with improved functions requires a deep understanding of how sequence and function are related, a vast space that is hard to explore. The ability to efficiently compress this space by identifying functionally important features is extremely valuable. Here we establish a method called EvoScan to comprehensively segment and scan the high-fitness sequence space to obtain anchor points that capture its essential features, especially in high dimensions. Our approach is compatible with any biomolecular function that can be coupled to a transcriptional output. We then develop deep learning and large language models to accurately reconstruct the space from these anchors, allowing computational prediction of novel, highly fit sequences without prior homology-derived or structural information. We apply this hybrid experimental–computational method, which we call EvoAI, to a repressor protein and find that only 82 anchors are sufficient to compress the high-fitness sequence space with a compression ratio of 10 48 . The extreme compressibility of the space informs both applied biomolecular design and understanding of natural evolution.

This is a preview of subscription content, access via your institution

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 12 print issues and online access

251,40 € per year

only 20,95 € per issue

Buy this article

• Purchase on SpringerLink
• Instant access to full article PDF

Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others

Low- N protein engineering with data-efficient deep learning

ECNet is an evolutionary context-integrated deep learning framework for protein engineering

The genetic architecture of protein stability

Data availability.

Source data are provided with this paper. Other data and materials used in this study are available from the corresponding authors by reasonable request. PDB files used in this study include PDB ID 7CB7 and PDB ID 7VLO . All the prediction features and results of mutants are available via Zenodo at https://doi.org/10.5281/zenodo.10686156 (ref. 61 ).

Code availability

The models of EvoAI are implemented in PyTorch v2.2.0. All codes are freely downloadable via Zenodo at https://doi.org/10.5281/zenodo.10686156 (ref. 61 ) or via GitHub at https://github.com/Gonglab-THU/EvoAI .

Lovelock, S. L. et al. The road to fully programmable protein catalysis. Nature 606 , 49–58 (2022).

Article   CAS   PubMed   Google Scholar  

Labanieh, L. & Mackall, C. L. CAR immune cells: design principles, resistance and the next generation. Nature 614 , 635–648 (2023).

Dumontet, C., Reichert, J. M., Senter, P. D., Lambert, J. M. & Beck, A. Antibody–drug conjugates come of age in oncology. Nat. Rev. Drug Discov. 22 , 641–661 (2023).

Macken, C. A. & Perelson, A. S. Protein evolution on rugged landscapes. Proc. Natl Acad. Sci. USA 86 , 6191–6195 (1989).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Lutz, S. Beyond directed evolution—semi-rational protein engineering and design. Curr. Opin. Biotechnol. 21 , 734–743 (2010).

Ding, X., Zou, Z. & Brooks, C. L. III Deciphering protein evolution and fitness landscapes with latent space models. Nat. Commun. 10 , 5644 (2019).

Tian, P. & Best, R. B. Exploring the sequence fitness landscape of a bridge between protein folds. PLoS Comput. Biol. 16 , e1008285 (2020).

Fernandez-de-Cossio-Diaz, J., Uguzzoni, G. & Pagnani, A. Unsupervised inference of protein fitness landscape from deep mutational scan. Mol. Biol. Evol. 38 , 318–328 (2021).

D’Costa, S., Hinds, E. C., Freschlin, C. R., Song, H. & Romero, P. A. Inferring protein fitness landscapes from laboratory evolution experiments. PLoS Comput. Biol. 19 , e1010956 (2023).

Article   PubMed   PubMed Central   Google Scholar  

Fowler, D. M. & Fields, S. Deep mutational scanning: a new style of protein science. Nat. Methods 11 , 801–807 (2014).

Stiffler, M. A., Hekstra, D. R. & Ranganathan, R. Evolvability as a function of purifying selection in TEM-1 β-lactamase. Cell 160 , 882–892 (2015).

Zheng, L., Baumann, U. & Reymond, J.-L. An efficient one-step site-directed and site-saturation mutagenesis protocol. Nucleic Acids Res. 32 , e115 (2004).

McLaughlin, R. N. Jr, Poelwijk, F. J., Raman, A., Gosal, W. S. & Ranganathan, R. The spatial architecture of protein function and adaptation. Nature 491 , 138–142 (2012).

Cadwell, R. C. & Joyce, G. F. Randomization of genes by PCR mutagenesis. Genome Res. 2 , 28–33 (1992).

Article   CAS   Google Scholar  

Vanhercke, T., Ampe, C., Tirry, L. & Denolf, P. Reducing mutational bias in random protein libraries. Anal. Biochem. 339 , 9–14 (2005).

Esvelt, K. M., Carlson, J. C. & Liu, D. R. A system for the continuous directed evolution of biomolecules. Nature 472 , 499–503 (2011).

Miller, S. M., Wang, T. & Liu, D. R. Phage-assisted continuous and non-continuous evolution. Nat. Protoc. 15 , 4101–4127 (2020).

Ravikumar, A., Arzumanyan, G. A., Obadi, M. K. A., Javanpour, A. A. & Liu, C. C. Scalable, continuous evolution of genes at mutation rates above genomic error thresholds. Cell 175 , 1946–1957.e1913 (2018).

Sarkisyan, K. S. et al. Local fitness landscape of the green fluorescent protein. Nature 533 , 397–401 (2016).

Hopf, T. A. et al. Mutation effects predicted from sequence co-variation. Nat. Biotechnol. 35 , 128–135 (2017).

Riesselman, A. J., Ingraham, J. B. & Marks, D. S. Deep generative models of genetic variation capture the effects of mutations. Nat. Methods 15 , 816–822 (2018).

Yang, K. K., Wu, Z. & Arnold, F. H. Machine-learning-guided directed evolution for protein engineering. Nat. Methods 16 , 687–694 (2019).

Luo, Y. et al. ECNet is an evolutionary context-integrated deep learning framework for protein engineering. Nat. Commun. 12 , 5743 (2021).

Wu, Z., Johnston, K. E., Arnold, F. H. & Yang, K. K. Protein sequence design with deep generative models. Curr. Opin. Chem. Biol. 65 , 18–27 (2021).

Somermeyer, L. G. et al. Heterogeneity of the GFP fitness landscape and data-driven protein design. eLife 11 , e75842 (2022).

Shen, M. W., Zhao, K. T. & Liu, D. R. Reconstruction of evolving gene variants and fitness from short sequencing reads. Nat. Chem. Biol. 17 , 1188–1198 (2021).

Biswas, S., Khimulya, G., Alley, E. C., Esvelt, K. M. & Church, G. M. Low-N protein engineering with data-efficient deep learning. Nat. Methods 18 , 389–396 (2021).

Papkou, A., Garcia-Pastor, L., Escudero, J. A. & Wagner, A. A rugged yet easily navigable fitness landscape. Science 382 , eadh3860 (2023).

Halperin, S. O. et al. CRISPR-guided DNA polymerases enable diversification of all nucleotides in a tunable window. Nature 560 , 248–252 (2018).

Baas, P. DNA replication of single-stranded Escherichia coli DNA phages. Biochim. Biophys. Acta Gene Struct. Expr. 825 , 111–139 (1985).

Jinek, M. et al. A programmable dual-RNA-guided DNA endonuclease in adaptive bacterial immunity. Science 337 , 816–821 (2012).

Ran, F. A. et al. Genome engineering using the CRISPR–Cas9 system. Nat. Protoc. 8 , 2281–2308 (2013).

Dietsch, F. et al. Small p53 derived peptide suitable for robust nanobodies dimerization. J. Immunol. Methods 498 , 113144 (2021).

Di Lallo, G., Castagnoli, L., Ghelardini, P. & Paolozzi, L. A two-hybrid system based on chimeric operator recognition for studying protein homo/heterodimerization in Escherichia coli . Microbiology 147 , 1651–1656 (2001).

Article   PubMed   Google Scholar  

Gao, K. et al. Perspectives on SARS-CoV-2 main protease inhibitors. J. Med. Chem. 64 , 16922–16955 (2021).

Li, J. et al. Structural basis of the main proteases of coronavirus bound to drug candidate PF-07321332. J. Virol. 96 , e02013–e02021 (2022).

Fu, L. et al. Both Boceprevir and GC376 efficaciously inhibit SARS-CoV-2 by targeting its main protease. Nat. Commun. 11 , 4417 (2020).

Owen, D. R. et al. An oral SARS-CoV-2 M pro inhibitor clinical candidate for the treatment of COVID-19. Science 374 , 1586–1593 (2021).

Iketani, S. et al. Functional map of SARS-CoV-2 3CL protease reveals tolerant and immutable sites. Cell Host Microbe 30 , 1354–1362 (2022).

Iketani, S. et al. Multiple pathways for SARS-CoV-2 resistance to nirmatrelvir. Nature 613 , 558–564 (2023).

Dickinson, B. C., Packer, M. S., Badran, A. H. & Liu, D. R. A system for the continuous directed evolution of proteases rapidly reveals drug-resistance mutations. Nat. Commun. 5 , 5352 (2014).

Packer, M. S., Rees, H. A. & Liu, D. R. Phage-assisted continuous evolution of proteases with altered substrate specificity. Nat. Commun. 8 , 956 (2017).

Blum, T. R. et al. Phage-assisted evolution of botulinum neurotoxin proteases with reprogrammed specificity. Science 371 , 803–810 (2021).

Duan, Y. et al. Molecular mechanisms of SARS-CoV-2 resistance to nirmatrelvir. Nature 622 , 376–382 (2023).

Nashed, N. T., Aniana, A., Ghirlando, R., Chiliveri, S. C. & Louis, J. M. Modulation of the monomer-dimer equilibrium and catalytic activity of SARS-CoV-2 main protease by a transition-state analog inhibitor. Commun. Biol. 5 , 160 (2022).

Stanton, B. C. et al. Genomic mining of prokaryotic repressors for orthogonal logic gates. Nat. Chem. Biol. 10 , 99–105 (2014).

Ramos, J. L. et al. The TetR family of transcriptional repressors. Microbiol. Mol. Biol. Rev. 69 , 326–356 (2005).

Nielsen, A. A. et al. Genetic circuit design automation. Science 352 , aac7341 (2016).

Brophy, J. A. N. & Voigt, C. A. Principles of genetic circuit design. Nat. Methods 11 , 508–520 (2014).

DeBenedictis, E. A. et al. Systematic molecular evolution enables robust biomolecule discovery. Nat. Methods 19 , 55–64 (2021).

Weinreich, D. M. & Chao, L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution 59 , 1175–1182 (2005).

CAS   PubMed   Google Scholar  

Weissman, D. B., Feldman, M. W. & Fisher, D. S. The rate of fitness-valley crossing in sexual populations. Genetics 186 , 1389–1410 (2010).

Dickinson, B. C., Leconte, A. M., Allen, B., Esvelt, K. M. & Liu, D. R. Experimental interrogation of the path dependence and stochasticity of protein evolution using phage-assisted continuous evolution. Proc. Natl Acad. Sci. USA 110 , 9007–9012 (2013).

Carlson, J. C., Badran, A. H., Guggiana-Nilo, D. A. & Liu, D. R. Negative selection and stringency modulation in phage-assisted continuous evolution. Nat. Chem. Biol. 10 , 216–222 (2014).

Green, M. R. & Sambrook, J. The Inoue method for preparation and transformation of competent Escherichia coli : “ultracompetent” cells. Cold Spring Harb. Protoc. 2020 , 101196 (2020).

Chen, R., Li, L. & Weng, Z. ZDOCK: an initial‐stage protein‐docking algorithm. Proteins Struct. Funct. Bioinf. 52 , 80–87 (2003).

Tamura, K., Stecher, G. & Kumar, S. MEGA11: molecular evolutionary genetics analysis version 11. Mol. Biol. Evol. 38 , 3022–3027 (2021).

Letunic, I. & Bork, P. Interactive Tree Of Life (iTOL) v5: an online tool for phylogenetic tree display and annotation. Nucleic Acids Res. 49 , W293–W296 (2021).

Liang, J. C., Chang, A. L., Kennedy, A. B. & Smolke, C. D. A high-throughput, quantitative cell-based screen for efficient tailoring of RNA device activity. Nucleic Acids Res. 40 , e154 (2012).

Xu, Y., Liu, D. & Gong, H. Improving the prediction of protein stability changes upon mutations by geometric learning and a pre-training strategy. Nat. Comput. Sci. https://doi.org/10.1038/s43588-024-00716-2 (2024).

Ma, Z. et al. EvoAI enables extreme compression and reconstruction of the protein sequence space. Zenodo https://doi.org/10.5281/zenodo.10686156 (2024).

Download references

Acknowledgements

This study was supported by Ministry of Science and Technology of China grant 2023YFA0915601 (S.Z.), National Natural Science Foundation of China grants U22A20552 (S.Z.) and 32171416 (S.Z.), Tsinghua University Dushi Plan Foundation (S.Z.), Beijing Frontier Research Center for Biological Structure (S.Z.) and US NIH R01 EB022376/EB031172 (D.R.L.) and R35 GM118062 (D.R.L.). We thank J. Zheng (Westlake University) for helpful discussions. We thank C. Zhang (Tsinghua University) for the kind gift of the EvolvR gene. We apologize to authors whose work cannot be cited owing to referencing restrictions.

Author information

These authors contributed equally: Ziyuan Ma, Wenjie Li, Yunhao Shen, Yunxin Xu.

Authors and Affiliations

School of Pharmaceutical Sciences, Tsinghua University, Beijing, China

Ziyuan Ma, Wenjie Li, Yunhao Shen, Gengjiang Liu, Jiamin Chang, Zeju Li, Hong Qin, Boxue Tian & Shuyi Zhang

School of Life Sciences, Tsinghua University, Beijing, China

Yunxin Xu & Haipeng Gong

State Key Laboratory of Molecular Oncology, School of Pharmaceutical Sciences, Tsinghua University, Beijing, China

Boxue Tian & Shuyi Zhang

Merkin Institute of Transformative Technologies in Healthcare, Broad Institute of MIT and Harvard, Cambridge, MA, USA

David R. Liu

Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA, USA

Howard Hughes Medical Institute, Harvard University, Cambridge, MA, USA

Department of Chemistry, Williams College, Williamstown, MA, USA

B. W. Thuronyi

Synthetic Biology Center, Department of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA

Christopher A. Voigt

Center for Synthetic and Systems Biology, Tsinghua University, Beijing, China

Shuyi Zhang

Beijing Frontier Research Center for Biological Structure, Tsinghua University, Beijing, China

You can also search for this author in PubMed   Google Scholar

Contributions

S.Z. conceptualized and supervised the project. S.Z., Z.M. and W.L. designed the experiments. Z.M., W.L. and H.Q. performed the evolution experiments in EvoScan. Z.M., W.L., Y.S. and Z.L. performed the flow cytometry assays and phage propagation assays of obtained variants. G.L. conducted the mammalian cell experiments. H.G., B.T., Y.X. and J.C. designed and developed the deep learning models. Z.M. and Y.S. wrote the first draft. B.W.T., D.R.L., C.A.V. and S.Z. wrote the final manuscript. All authors contributed to the drafting and revision of the manuscript.

Corresponding author

Correspondence to Shuyi Zhang .

Ethics declarations

Competing interests.

S.Z. and Z.M. have filed a patent application based on this work. The other authors declare no competing interests.

Peer review

Peer review information.

Nature Methods thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Arunima Singh, in collaboration with the Nature Methods team. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended data fig. 1 pance for egfp-nanobody..

( a ) Genetic circuit design of PANCE for EGFP-nanobody. ( b ) Diagram of PANCE process for EGFP-nanobody. ( c ) Phage propagation assays of the cI-mutation nanobody compared to WT and ΔgIII. ( d ) Flow cytometry assays of interaction between the mutated cIp22 and the WT cI434. Concentration of IPTG was 0, 50, 100, 200, 500 and 1000 μM. Data are mean ± SD of three experiments.

Source data

Extended data fig. 2 the protease activity testing system..

( a ) Schematic diagram of reverse two-hybrid protease activity testing system. Matched substrate was used as the linker of the cI repressor pair, and the active protease cut the substrate and rescued the activity of the p434 promoter repressed by the fused cI repressor. Expression of the downstream reporters (fluorescence protein, pIII for phage propagation, etc.) was controlled by the p434 promoter. ( b ) Flow cytometry assays for HCV protease by the reverse two-hybrid protease activity testing system. Different concentrations of vanillic acid (0, 50, 100, 200 μM) and IPTG (100 μM) were used. ( c ) Schematic diagram of the T7-based protease activity testing system. T7 lysozyme and T7 polymerase were linked together with a linker carrying the protease substrate. As the protease cut the substrate, released T7 polymerase recognized T7 promoter and expressed the downstream reporter. ( d ) Flow cytometry assays for M pro by T7-based protease activity system (IPTG = 100, 200 μM, Vanillic acid=0, 50, 100, 200 μM). ( e ) Phage propagation assays for M pro and its variants under different concentrations of IPTG (IPTG = 0, 100, 200, 500, 1000 μM). ( f ) Phage propagation assays for inhibitors with different concentrations. Inhibitor concentration gradient was set as 0, 5, 10, 20, 40 μM. The concentration of IPTG was set as 1000 μM. ( g ) Flow cytometry assays for representative M pro variants obtained by EvoScan (IPTG = 100 μM, vanillic acid=100 μM, GC376 = 50 μM, PF-07321332 = 50 μM). ( h ) Resistance Index of M pro variants on both inhibitors (50 μM). Concentration of IPTG was 100 μM, and vanillic acid was 100 μM. Data are mean ± SD of three experiments.

Extended Data Fig. 3 PANCE to obtain M pro variants that escape the inhibition of GC376.

( a ) Genetic circuit design of PANCE for M pro . ( b ) Diagram of PANCE process for M pro . 4 replication groups were performed. ( c ) Evolution results of PANCE after 96 passages. ( d ) Flow cytometry assays of M pro variants. The A191V and N119D single mutation were also measured and served as control groups. Concentration of IPTG was 100 μM, concentration of vanillic acid was 100 μM, and concentration of GC376 was 50 μM. ( e ) Resistance Index of variants against GC376 after 96 passages. The A191V and N119D single mutation were also shown as control groups. ( f ) Mutations from PANCE mapped to the crystal structure of M pro (PDB ID: 7CB7 ). Data are mean ± SD of three experiments.

Extended Data Fig. 4 PANCE for AmeR evolution.

( a ) Genetic circuit design of PANCE for AmeR evolution. ( b ) Propagation assays of combinatorial AP designs. Different RBS combinations for PhlF and gIII on APs were tested. ( c ) Workflow of PANCE for AmeR. 12 replication groups were performed. ( d ) Evolution results of PANCE for AmeR after 16 passages. ( e ) Flow cytometry assay of variants from PANCE for AmeR. Data are mean ± SD of three experiments.

Extended Data Fig. 5 AmeR variant activity measurement and evolution path analysis.

( a ) Fold repression of 82 AmeR variants from EvoScan. Data are mean ± SD of three experiments. The circuit for flow cytometry assay was shown. ( b ) Possible evolutionary paths that lead to the same variants with multiple mutations.

Extended Data Fig. 6 Genetic circuit construction with WT AmeR and the S57R variant.

( a ) Schematic diagram of AmeR flow cytometry assay in mammalian cell (HEK293T). ( b ) The genetic circuit for AmeR flow cytometry assay and the results. 6 M is the AmeR variant R43G A53T S57R A75V P94L D119N. ( c ) Genetic circuit design of A IMPLY B. ( d ) Flow cytometry assay of the genetic circuit A IMPLY B. ( e ) Genetic circuit design of A NIMPLY B. ( f ) Flow cytometry assay of the genetic circuit A NIMPLY B. ( g ) Genetic circuit design of NAND. ( h ) Flow cytometry assay of the genetic circuit NAND. All circuits in this figure used 100 μM vanillic acid (input A) and 1000 μM IPTG (input B) as input signals. Data are mean ± SD of three experiments.

Extended Data Fig. 7 Overall algorithm flow of the GeoFitness geometric encoder.

For each protein variant, sequence information was transferred into a 1-dimensional vector, and the structure of the sample collected from PDB or predicted by Alphafold2 was transferred into a 2-dimensional vector. These two inputs were integrated through the geometric encoder block and the output was put into the Multi-Layer Perceptron (MLP) for generation of predicted fitness.

Extended Data Fig. 8 Cross-Validation of EvoAI model training.

( a ) Schematic diagram of the data set in 10-fold cross-validation. ( b ) CV-test spearman correlation coefficient of different layers during cross-validation. Curves are shown as the mean of 10 groups. The shadow shows the 95% confidence interval of Spearman correlation values among training process. ( c ) Influence of layer number of MLP on 10-fold cross-validation of model training. 2-layer MLP shows the best performance with higher spearman correlation coefficient compared to 1-layer MLP and smaller variance compared to 3-layer MLP. The centre line represented the median value, while the box contained a quarter to three quarters of the dataset. The minima and maxima were also shown by the whiskers.

Extended Data Fig. 9 GeoFitness values of AmeR mutations.

( a ) GeoFitness values of all single site mutations generated by the pre-trained model. The first 28 sites of N-terminal were discarded in prediction because of low confidence. A larger score indicates a higher likelihood that this mutation will improve protein function. ( b ) GeoFitness value ranking of mutations from all the anchors. The selected top 11 sites (13 mutations in total) were colored in red. ( c ) Predicted score of the top 10 variants each with a combination of 6 mutations designed by EvoAI. ( d ) Spearman correlation coefficient of the predicted fold repression rank and the experimental fold repression rank of the top 10 variants. The shaded area around the fitted line represents the 95% confidence interval. ( e ) Top 15 mutations with the highest predicted GeoFitness values from all single mutations. ( f ) Experimental fold repression of the designed variants using model trained by EvoScan anchors (Top, Middle, Bottom) or deep mutational scanning (DMS) information. Data points are mean of three biological replicates. The centre line represented the median value, while the box contained a quarter to three quarters of the dataset. The minima and maxima were also shown by the whiskers. ( g ) AUPRC plot for EvoAI-generated variants. ( h ) AUPRC plot for the test set during EvoAI training.

Supplementary information

Supplementary information.

Supplementary Tables 1–7.

Reporting Summary

Peer review file, source data fig. 1.

Statistical source data.

Source Data Fig. 2

Source data fig. 3, source data fig. 4, source data fig. 5, source data extended data fig./table 1, source data extended data fig./table 2, source data extended data fig./table 3, source data extended data fig./table 4, source data extended data fig./table 5, source data extended data fig./table 6, source data extended data fig./table 8, source data extended data fig./table 9, rights and permissions.

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Cite this article.

Ma, Z., Li, W., Shen, Y. et al. EvoAI enables extreme compression and reconstruction of the protein sequence space. Nat Methods (2024). https://doi.org/10.1038/s41592-024-02504-2

Download citation

Received : 05 February 2024

Accepted : 10 October 2024

Published : 11 November 2024

DOI : https://doi.org/10.1038/s41592-024-02504-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Advertisement

Hybrid rainfall–runoff model with continuous infiltration experiments: a Mediterranean coastal basin of Madjez Ressoul in Algeria

• Original Paper
• Published: 08 November 2024

Cite this article

• Asma Dahak   ORCID: orcid.org/0000-0002-1011-3012 1 ,
• Hamouda Boutaghane 1 ,
• Tarek Merabtene 2 ,
• Sameh Ahmed Kantoush 3 ,
• Tayeb Boulmaiz 4 ,
• Mohamed Saber 3 &
• Tetsuya Sumi 3  

Explore all metrics

The Madjez Ressoul watershed, located in Algeria (A = 103 km 2 ), provides a unique opportunity to investigate the accurate prediction of flood hydrographs in a natural setting and relatively untouched environment. Its particularity is an excellent option for simplified rainfall–runoff models due to the potential reduction in model complexity and data requirements. This study applies the Hydrologic Engineering Center’s Hydrologic Modeling System model to simulate 36 year rainfall–runoff modeling (1973–2009). The originality of this study lies in employing experimental infiltration data to improve rainfall–runoff prediction. The study offers valuable insights into the hydrological behavior of the Madjez Ressoul watershed by integrating advanced methods and tools when analyzing hydrological responses. Effective calibration refines the model’s ability to predict flow dynamics by adjusting various parameters. Various methods were selected to simulate hydrological processes, including the soil conservation service-curve Number, SCS unit hydrograph, Muskingum, recession baseflow, and channel loss. The model was tested on many continuous events, and the results revealed a good fit between the simulated and observed discharge data. This evaluation was performed using four criteria (the Nash Sutcliff test, root mean square error, percent bias, and correlation coefficient), indicating reasonable accuracy of the model correlation. Using the findings of this study can aid in providing a better knowledge of water flow dynamics in the Madjez Ressoul watershed by opening up new possibilities to inform the development of flood risk management techniques that have the potential to mitigate the adverse effects of floods on the environment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Rainfall-runoff modeling: flow characterization of Hammam Melouane Wadi Algeria

Rainfall-runoff modeling considering soil moisture accounting algorithm, case study: Karoon III River basin

Performance of rainfall–runoff models in reproducing hydrological extremes: a case of the River Malaba sub-catchment

Aksoy H, Gedikli A, Unal NE, Yilmaz M, Eris E, Yoon J, Tayfur G (2016) Rainfall–runoff model considering microtopography simulated in a laboratory erosion flume. Water Resour Manag 30:5609–5624

Article   Google Scholar  

AL-AreeqSharifAbbaChowdhuryAl-SuwaiyanBenaafiAljundi AMHOSSMMIH (2023) Digital elevation model for flood hazards analysis in complex terrain: case study from Jeddah, Saudi Arabia. Int J Appl Earth Obs Geoinf 119:103330

Google Scholar  

Areri DC, Bibi TS (2023) Identification of small-scale hydropower potential sites using geographic information system and hydrologic modeling technique: Awata river, Genale Dawa basin, Ethiopia. Energy Rep 9:2405–2419

Bhuiyan HA, McNairn H, Powers J, Merzouki A (2017) Application of HEC-HMS in a cold region watershed and use of RADARSAT-2 soil moisture in initializing the model. Hydrology 4(1):9

Birkel C, Barahona AC (2019) Rainfall-runoff modeling: a brief overview. Ref Module Earth Syst Environ Sci

Brocca L, Melone F, Moramarco T (2011) Distributed rainfall‐runoff modelling for flood frequency estimation and flood forecasting. Hydrol Process 25(18):2801–2813

Cacal JC, Austria VCA, Taboada EB (2023) Extreme Event-based Rainfall-runoff Simulation Utilizing GIS Techniques in Irawan Watershed, Palawan, Philippines. Civil Eng J 9(1):220–232

Castro CV, Maidment DR (2020) GIS preprocessing for rapid initialization of HEC-HMS hydrological basin models using web-based data services. Environ Model Softw 130:104732

Cea L, Garrido M, Puertas J (2010) Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J Hydrol 382(1–4):88–102

Chakravarti A, Jain MK (2014) Experimental invesitigation and modeling of rainfall runoff process. Indian J Sci Technol 7(12):2096

Chandwani V, Vyas SK, Agrawal V, Sharma G (2015) Soft computing approach for rainfall-runoff modelling: a review. Aquat Procedia 4:1054–1061

Chu X, Steinman A (2009) Event and continuous hydrologic modeling with HEC-HMS. J Irrig Drain Eng 135(1):119–124

Dahak A, Boutaghane H, Merabtene T (2022) Parameter estimation and assessment of infiltration models for Madjez Ressoul catchment, Algeria. Water 14(8):1185

Danáčová M, Valent P, Výleta R (2017) Evaluation of surface runoff generation processes using a rainfall simulator: a small scale laboratory experiment. Paper presented at the IOP Conference Series: Earth and Environmental Science

Dariane AB, Javadianzadeh M, James LD (2016) Developing an efficient auto-calibration algorithm for HEC-HMS program. Water Resour Manag 30:1923–1937

Dastorani MT, Khodaparast R, Talebi A, Vafakhah M, Dashti J (2011) Determination of the ability of HEC-HMS model components in rainfall-run-off simulation. Res J Environ Sci 5(10):790

Dimri T, Ahmad S, Sharif M (2023) Hydrological modelling of Bhagirathi river basin using HEC-HMS. J Appl Water Eng Res 11(2):249–261

Du J, Xie S, Xu Y, Xu C-y, Singh VP (2007) Development and testing of a simple physically-based distributed rainfall-runoff model for storm runoff simulation in humid forested basins. J Hydrol 336(3–4):334–346

Frysali D, Mallios Z, Theodossiou N (2023) Hydrologic modeling of the Aliakmon river in Greece using HEC–HMS and open data. Euro-Mediterr J Environ Integ 8:539–555

Gao X, Yang Z, Han D, Gao K, Zhu Q (2021) The impact of wind on the rainfall–runoff relationship in urban high-rise building areas. Hydrol Earth Syst Sci 25(11):6023–6039

Goyal A, Flammini A, Morbidelli R, Corradini C, Govindaraju RS (2023) Role of in-situ point instruments in the estimation of variability in soil saturated hydraulic conductivity. Hydrol Sci J 68(3):448–461

Guduru JU, Jilo NB, Rabba ZA, Namara WG (2023) Rainfall–runoff modeling using HEC-HMS model for Meki river watershed, rift valley basin. Ethiop J Afr Earth Sci 197:104743

Halwatura D, Najim M (2013) Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ Model Softw 46:155–162

Hou L, Feng S, Huo Z, Ding Y, Zhang S (2008) Experimental study on rainfall–runoff relation for porous pavements. Hydrol Res 39(3):181–190

Janicka E, Kanclerz J, Agaj T, Gizińska K (2023) Comparison of two hydrological models, the HEC-HMS and nash models, for runoff estimation in Michałówka river. Sustainability 15(10):7959

Jones R, Thomas RE, Peakall J, Manville V (2017) Rainfall–runoff properties of tephra: simulated effects of grain-size and antecedent rainfall. Geomorphology 282:39–51

Joo J, Kjeldsen T, Kim H-J, Lee H (2014) A comparison of two event-based flood models (ReFH-rainfall runoff model and HEC-HMS) at two Korean catchments, Bukil and Jeungpyeong. KSCE J Civil Eng 18:330–343

Kaberia LG, Mundia CN, Makokha GO, Kimwatu DM (2023) Simulation and prediction of sediment loads using MUSLE–HEC-HMS model in the Upper Ewaso Nyiro River Basin, Kenya. Model Earth Syst Environ. 9:1–15

Kamali B, Mousavi SJ, Abbaspour K (2013) Automatic calibration of HEC-HMS using single-objective and multi-objective PSO algorithms. Hydrol Process 27(26):4028–4042

Khaerudin DN, Suharyanto A, Harisuseno D (2017) Infiltration rate for rainfall and runoff process with bulk density soil and slope variation in laboratory experiment. Nat Environ Pollut Technol. 16(1)

Khanaum MM, Borhan MS (2023) Effects of increasing rainfall depths and impervious areas on the hydrologic responses. Open J Mod Hydrol 13(2): 114–128

Langhans C, Govers G, Diels J, Leys A, Clymans W, Vandenputte A, Valckx J (2009) Experimental rainfall–runoff data: the concept of infiltration capacity needs re-thinking. Paper presented at the EGU General Assembly Conference Abstracts

Lamb R, Faulkner D, Wass P, Cameron D (2016) Have applications of continuous rainfall–runoff simulation realized the vision for process-based flood frequency analysis? Hydrol Process 30(14):2463–2481

Liu W, Feng Q, Deo RC, Yao L, Wei W (2020) Experimental study on the rainfall–runoff responses of typical urban surfaces and two green infrastructures using scale-based models. Environ Manag 66:683–693

Mai Y, Zhang M, Chen W, Chen X, Huang G, Li D (2018) Experimental study on the effects of LID measures on the control of rainfall runoff. Urban Water J 15(9):827–836

Article   CAS   Google Scholar  

Matthew JF, James HD (2013) HEC-GeoHMS geospatial hydrologic modeling extension

Meißl G, Klebinder K, Zieher T, Lechner V, Kohl B, Markart G (2023) Influence of antecedent soil moisture content and land use on the surface runoff response to heavy rainfall simulation experiments investigated in Alpine catchments. Heliyon 9(8):e18597

Meng X, Zhu Y, Shi R, Yin M, Liu D (2024) Rainfall–runoff process and sediment yield in response to different types of terraces and their characteristics: a case study of runoff plots in Zhangjiachong watershed. China Land Degrad Dev 35:1449–1465

Mobarhan EY, Sangchini EK (2021) Continuous rainfall–runoff modeling using HMS-SMA with emphasis on the different calibration scale. J Chin Soil Water Conserv 52(2):112–119

Morbidelli R, Saltalippi C, Flammini A, Cifrodelli M, Picciafuoco T, Corradini C, Govindaraju RS (2017) In situ measurements of soil saturated hydraulic conductivity: assessment of reliability through rainfall–runoff experiments. Hydrol Process 31(17):3084–3094

Moon H, Yoon S, Moon Y (2023) Urban flood forecasting using a hybrid modeling approach based on a deep learning technique. J Hydroinformatics 25(2):593–610

Naqash TB, Ahanger MA, Maity R (2023) Multi-site hydrometeorological simulation of streamflow for upper Jhelum basin in northwest Himalayas using HEC–HMS soil moisture accounting algorithm. Model Earth Syst Environ 9(1):431–455

Olotu Y, Olanrewaju OO, Rodiya AA, Adekunle AP (2022) Experimental study of rainfall–runoff process through calibrated simulator; a case study of Auchi Polytechnic, Auchi, Edo state, Nigeria. Int J Earth Sci Knowl Appl 4(2):250–258

Ortega JP, Cambronero L, Alcarria SM et al (2024) Conducting an in situ evaluation of erodibility in a Mediterranean semi-arid and conventional vineyard in Granada province (Southern Spain) through rainfall simulation experiments. Euro-Mediterr J Environ Integ 9:797–808

Patel S, Verma P, Singh G (2019) Agricultural growth and land use land cover change in peri-urban India. Environ Monit Assess. https://doi.org/10.1007/s10661-019-7736-1

Petkov P (2021) Using the double-ring infiltrometer to evaluate key unsaturated and saturated hydrological properties. Water Resour Res 14:601–604

Ran Q, Su D, Li P, He Z (2012) Experimental study of the impact of rainfall characteristics on runoff generation and soil erosion. J Hydrol 424:99–111

Ren DF, Cao AH (2023) Precipitation–runoff simulation in Xiushui river basin using HEC–HMS hydrological model. Model Earth Syst Environ 9:1–12

Romali N, Yusop Z, Ismail A (2018) Hydrological modelling using HEC-HMS for flood risk assessment of Segamat Town, Malaysia. In: IOP Conference Series: Materials Science and Engineering

Salhi H (2022) Evaluation of the spatial distribution of the annual extreme precipitation using kriging and co-kriging methods in algeria country. Climate change in Asia and Africa: examining the biophysical and social consequences, and society’s responses. IntechOpen, London

Salhi H, Hadjira A, Belkhiri L, Tiri A, Mouni L (2024) Evaluation of the spatial distribution of the extreme rainfall across Algeria country. Environ Earth Sci 83:440

Sampath D, Weerakoon S, Herath S (2015) HEC-HMS model for runoff simulation in a tropical catchment with intra-basin diversions case study of the Deduru Oya River Basin, Sri Lanka

Samuel J, Coulibaly P, Metcalfe RA (2012) Identification of rainfall–runoff model for improved baseflow estimation in ungauged basins. Hydrol Process 26(3):356–366

Sanjay Shekar N, Vinay D (2021) Performance of HEC-HMS and SWAT to simulate streamflow in the sub-humid tropical Hemavathi catchment. J Water Clim Change 12(7):3005–3017

Sayed BT, Al-Mohair HK, Alkhayyat A, Ramírez-Coronel AA, Elsahabi M (2023) Comparing machine-learning-based black box techniques and white box models to predict rainfall-runoff in a northern area of Iraq, the Little Khabur River. Water Sci Technol 87(3):812–822

Shokri A (2023) Development of a new event-based rainfall-runoff equation based on average rainfall intensity during an event. Environ Model Assess 28:1-14

Sidiras N, Roth C (1987) Infiltration measurements with double-ring infiltrometers and a rainfall simulator under different surface conditions on an Oxisol. Soil Tillage Res 9(2):161–168

Sihag P, Singh B (2018) Field evaluation of infiltration models. Tech Ecol Saf 11:1–11. https://doi.org/10.5281/zenodo.1239447

Sihag P, Singh B, Vand AS, Mehdipour V (2018) Modeling the infiltration process with soft computing techniques. ISH J Hydraul Eng 26(2):138–152. https://doi.org/10.1080/09715010.2018.1464408

Sitterson J, Knightes C, Parmar R, Wolfe K, Avant B, Muche M (2018) An overview of rainfall-runoff model types

Shahani MH, Rezaverdinejad V, Hosseini SA, Azad N (2023) Assessing climate change impact on river flow extreme events in different climates of Iran using hybrid application of LARS-WG6 and rainfall-runoff modeling of deep learning. Ecohydrology Hydrobiol 23(2):224–239

Skaggs RW, Khaleel R(1982) Hydrologic modeling of small watersheds

Snieder E, Khan UT (2023) A novel ensemble algorithm based on hydrological event diversity for urban rainfall–runoff model calibration and validation. J Hydrol 619:129193

Song S, Wang W (2019) Impacts of antecedent soil moisture on the rainfall–runoff transformation process based on high-resolution observations in soil tank experiments. Water 11(2):296

Soulis KX, Valiantzas J (2012) SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds–the two-CN system approach. Hydrol Earth Syst Sci 16(3):1001–1015

Touma J, Albergel J (1992) Determining soil hydrologic properties from rain simulator or double ring infiltrometer experiments: a comparison. J Hydrol 135(1–4):73–86

Vergroesen T, Man Joshi U, Van de Giesen N, Van de Ven F (2010) High resolution rainfall–runoff measurement setup for green roof experiments in a tropical environment. Hydrol Earth Syst Sci Discuss 7(6):9367–9410

Weiler M, Leistert H, Schmit M, Steinbrich A (2023) Linking in-situ and simulated soil moisture data for flood prediction: the advantage of joint probabilities of initial soil moisture and rainfall characteristic, EGU general assembly. Copernicus Meetings, Vienna, pp EGU23-16866

Wu L, Long T-Y, Liu X, Guo J-S (2012) Impacts of climate and land-use changes on the migration of non-point source nitrogen and phosphorus during rainfall-runoff in the Jialing River Watershed, China. J Hydrol 475:26–41

Wu S-J, Kuo C-Y, Yeh K-C, Wang C-D, Wang W-J (2021) Reliability analysis for reservoir water supply due to uncertainties in hydrological factors, rainfall-runoff routing and operating rule curves. J Hydro-Environment Res 34:24–45

Yersaw BT, Chane MB (2024) Regional climate models and bias correction methods for rainfall–runoff modeling in Katar watershed. Ethiop Environ Syst Res 13(1):10

Zhao N, Yu F, Li C, Wang H, Liu J, Mu W (2014) Investigation of rainfall–runoff processes and soil moisture dynamics in grassland plots under simulated rainfall conditions. Water 6(9):2671–2689

Zhu S, Wei J, Zhang H, Xu Y, Qin H (2023) Spatiotemporal deep learning rainfall–runoff forecasting combined with remote sensing precipitation products in large scale basins. J Hydrol 616:128727

Download references

Author information

Authors and affiliations.

Department of Hydraulics, Soil and Hydraulics Laboratory, Badji Mokhtar University, P.O. Box 12, Annaba, Algeria

Asma Dahak & Hamouda Boutaghane

Department of Civil and Environmental Engineering, University of Sharjah, P.O. Box 27272, Sharjah, United Arab Emirates

Tarek Merabtene

Water Resources Research Center–Disaster Prevention Research Institute, Kyoto University Goka-sho, Uji City, Kyoto, 611-0011, Japan

Sameh Ahmed Kantoush, Mohamed Saber & Tetsuya Sumi

Department of Hydraulics and Civil Engineering, University of Ghardaia, PO Box 455, 47000, Ghardaia, Algeria

Tayeb Boulmaiz

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Asma Dahak .

Ethics declarations

Conflict of interest.

The authors declare that they have non-financial interests that are directly or indirectly related to the work submitted for publication.

Additional information

Responsible Editor: Abdelwaheb Aydi.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Dahak, A., Boutaghane, H., Merabtene, T. et al. Hybrid rainfall–runoff model with continuous infiltration experiments: a Mediterranean coastal basin of Madjez Ressoul in Algeria. Euro-Mediterr J Environ Integr (2024). https://doi.org/10.1007/s41207-024-00674-1

Download citation

Received : 05 June 2024

Accepted : 06 October 2024

Published : 08 November 2024

DOI : https://doi.org/10.1007/s41207-024-00674-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Continuous simulation
• Madjez Ressoul watershed
• Numerical modeling
• Parameter estimation
• Rainfall–runoff
• Find a journal
• Publish with us
• Track your research

Help | Advanced Search

Computer Science > Computer Vision and Pattern Recognition

Title: hstrack: bootstrap end-to-end multi-camera 3d multi-object tracking with hybrid supervision.

Abstract: In camera-based 3D multi-object tracking (MOT), the prevailing methods follow the tracking-by-query-propagation paradigm, which employs track queries to manage the lifecycle of identity-consistent tracklets while object queries handle the detection of new-born tracklets. However, this intertwined paradigm leads the inter-temporal tracking task and the single-frame detection task utilize the same model parameters, complicating training optimization. Drawing inspiration from studies on the roles of attention components in transformer-based decoders, we identify that the dispersing effect of self-attention necessitates object queries to match with new-born tracklets. This matching strategy diverges from the detection pre-training phase, where object queries align with all ground-truth targets, resulting in insufficient supervision signals. To address these issues, we present HSTrack, a novel plug-and-play method designed to co-facilitate multi-task learning for detection and tracking. HSTrack constructs a parallel weight-share decoder devoid of self-attention layers, circumventing competition between different types of queries. Considering the characteristics of cross-attention layer and distinct query types, our parallel decoder adopt one-to-one and one-to-many label assignment strategies for track queries and object queries, respectively. Leveraging the shared architecture, HSTrack further improve trackers for spatio-temporal modeling and quality candidates generation. Extensive experiments demonstrate that HSTrack consistently delivers improvements when integrated with various query-based 3D MOT trackers. For example, HSTrack improves the state-of-the-art PF-Track method by $+2.3\%$ AMOTA and $+1.7\%$ mAP on the nuScenes dataset.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .