assignment 4.3 physics class 11

NCERT Solutions for Class 11th: Ch 4 Motion In A Plane Physics

Ncert solutions for class 11th: ch 4 motion in a plane physics science.

Contact Form

Talk to our experts

1800-120-456-456

• NCERT Exemplar for Class 11 Physics Chapter 4 - Motion in a Plane (Book Solutions)
• Textbook Solutions

NCERT Exemplar for Class 11 Physics - Motion in a Plane - Free PDF Download

Free PDF download of NCERT Exemplar for Class 11 Physics Chapter 4 - Motion in a Plane solved by expert Physics teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter 4 - Motion in a Plane exercise questions with solutions to help you to revise the complete syllabus and score more marks in your examinations.

Access NCERT Exemplar Solutions for Class 11 Physics Chapter 4 - Motion in a Plane

Multiple choice questions (type - i).

4.1. The angle between $\overrightarrow A  = \widehat i + \widehat j$ and $\overrightarrow B  = \widehat i - \widehat j$ is

Ans: Option (b) 

Since we know that, the angle between two vectors is given by

$ \Rightarrow \cos \theta  = \dfrac{{\overrightarrow A  \cdot \overrightarrow B }}{{\left| A \right|\left| B \right|}}$

$ \Rightarrow \cos \theta  = \dfrac{{1 - 1}}{{\sqrt 2  \cdot \sqrt 2 }} = \dfrac{0}{2} = 0$

$ \Rightarrow \theta  = 90^\circ $

Hence, the correct answer is (b).

4.2. Which one of the following statements is true?

(a) A scalar quantity is the one that is conserved in a process.

(b) A scalar quantity is the one that can never take negative values.

(c) A scalar quantity is the one that does not vary from one point to another in space.

(d) A scalar quantity has the same value for observers with different orientations of the axes.

Ans: Option (d) 

A scalar quantity has no direction hence it is the same when observed with different orientations of the axes. Hence, the correct answer is (d).

4.3. Figure shows the orientation of two vectors $\overrightarrow u $ and $\overrightarrow v $ in the X-Y plane.

If $\overrightarrow u  = a\widehat i + b\widehat j$ and $\overrightarrow v  = p\widehat i + q\widehat j$ ,

Which of the following is correct?

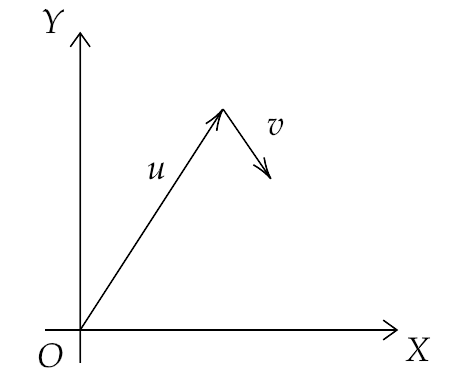
(a) a and p are positive while b and q are negative.

(b) a, p and b are positive while q is negative.

(c) a, q and b are positive while p is negative.

(d) a, b, p and q are all positive.

Since a, b and p, q are the components of X and Y direction and we can see that the second vector moving down and forwards, hence the Y-component of vector $\overrightarrow v $ , i.e. q is negative. The rest are positive. Hence, the correct answer is (b).

4.4. The component of vector r along X-axis will have maximum value if:

(a) $\overrightarrow r $ is along the positive Y-axis.

(b) $\overrightarrow r $ is along the positive X-axis.

(c) $\overrightarrow r $ makes an angle of 45⁰ with X-axis.

(d) $\overrightarrow r $ is along the negative Y-axis.

Since the value of $\cos {\theta _{\max }} = 1$ occurs when $\theta  = 0^\circ $ , therefore  it can happen only when $\overrightarrow r $ is along the positive X-axis. Hence, the correct answer is (b).

4.5. The horizontal range of a projectile fired at an angle of 15⁰ is 50m. If it is fired with the same at an angle of 45⁰, its range will be:

Ans: Option (c) 

Given that the horizontal range is 50m.

Therefore, we have

$ \Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$

$ \Rightarrow 50 = \dfrac{{{u^2}\sin 2 \times 15^\circ }}{g}$

That gives,

$ \Rightarrow {u^2} = 100g$

Now if we have $\theta  = 45^\circ $ , then

$ \Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g} = \dfrac{{100g \cdot \sin 2 \times 45^\circ }}{g} = 100m$

Hence, the correct answer is (c).

4.6. Consider the quantities, pressure, power, energy impulse, gravitational potential, electric charge, temperature, area. Out of these, the only vector quantities are:

(a) Impulse, pressure and area

(b) Impulse and area

(c) Area and gravitational constant

(d) Impulse and pressure

In the above given quantities only energy impulse and area are vector quantities and the rest are scalar quantities as they have no direction. Hence, the correct answer is (b).

4.7. In a two dimensional motion, instantaneous speed vₒ is positive, constant. Then which of the following are necessarily true?

(a) The average velocity is not zero at any time.

(b) Average acceleration must always vanish.

(c) Displacements in equal time intervals are equal.

(d) Equal path lengths are traversed in equal intervals.

If the instantaneous speed vₒ is positive and constant in a two dimensional motion, then due to the scalar nature of speed equal path lengths are traversed in equal intervals. Hence, the correct answer is (d).

4.8. In a two-dimensional motion, instantaneous speed $v_0$ is positive and constant. Then which of the following are necessarily true?

(a) The acceleration of a particle is zero.

(b) The acceleration of the particle is bounded.

(c) The acceleration of the particle is necessarily in the plane of motion.

(d) The particle must be undergoing a uniform circular motion.

The acceleration of the particle will necessarily be zero and in the plane of motion because the given speed is constant and positive, i.e. in the direction of force. Hence, the correct answer is (c).

4.9. Three vectors $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ add up to zero. Find which is false.

(a) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ is not zero unless $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel.

(b) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C $ is not zero unless $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel.

(c) If $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ define a place, $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ is in that plane.

(d) $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| \geqslant \left| {\overrightarrow C } \right| \Rightarrow {C^2} = {A^2} + {B^2}$

Ans: Options (b) and (d) 

Given that, $\overrightarrow A  + \overrightarrow B  + \overrightarrow C  = 0$

Now for (a), we can write

$ \Rightarrow \overrightarrow B  \times \left( {\overrightarrow A  + \overrightarrow B  + \overrightarrow C } \right) = \overrightarrow {\rm B}  \times 0$

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  + \overrightarrow B  \times \overrightarrow B  + \overrightarrow B  \times \overrightarrow C  = 0$

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  + 0 + \overrightarrow B  \times \overrightarrow C  = 0$

That gives us,

$ \Rightarrow \overrightarrow B  \times \overrightarrow A  =  - \overrightarrow B  \times \overrightarrow C $

$ \Rightarrow \overrightarrow A  \times \overrightarrow B  = \overrightarrow B  \times \overrightarrow C $

Now, that gives us,

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = \left( {\overrightarrow B  \times \overrightarrow C } \right) \times \overrightarrow C $

Now if $\overrightarrow B {\text{ and }}\overrightarrow C $ are parallel or antiparallel, then we have

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = \left| {BC\sin 0^\circ } \right| \times \overrightarrow C $

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C  = 0$

So option (a) is true.

Option (b) is false because $\left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C $ is always zero without $\overrightarrow B {\text{ and }}\overrightarrow C $ being parallel if we take $\overrightarrow A  \times \overrightarrow B  = \overrightarrow B  \times \overrightarrow C  = \overrightarrow P $ then we have $\overrightarrow P  \cdot \overrightarrow C  = 0$ because both vectors are perpendicular.

Now for option (c), if we have  $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $ in the same plane,   $\left( {\overrightarrow A  \times \overrightarrow B } \right)$ will be perpendicular to that plane, and then the vector $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ will be perpendicular to both $\left( {\overrightarrow A  \times \overrightarrow B } \right)$ and $\overrightarrow C $ and hence the vector   $\left( {\overrightarrow A  \times \overrightarrow B } \right) \times \overrightarrow C $ will lie in the original plane containing $\overrightarrow A $ , $\overrightarrow B $ and $\overrightarrow C $. So option (c) is true.  

For option (d) we have ${C^2} = {A^2} + {B^2}$

That means the angle between $\overrightarrow A $ and $\overrightarrow B $ is $90^\circ $ .

Now, we can write,

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left( {\left| A \right|\left| B \right|\sin 90^\circ } \right) \cdot \overrightarrow C $

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| A \right|\left| B \right|\left| C \right|\cos \theta $

$ \Rightarrow \left( {\overrightarrow A  \times \overrightarrow B } \right) \cdot \overrightarrow C  = \left| A \right|\left| B \right|\left| C \right|\cos \theta  \ne \left| A \right|\left| B \right|\left| C \right|$

So option (d) is false.

Hence, the correct answers are (b) and (d).

4.10. It is found that $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$ , this necessarily implies

(a) $\overrightarrow B  = 0$

(b) $\overrightarrow A ,\overrightarrow B $ are anti-parallel

(c) $\overrightarrow A ,\overrightarrow B $ are perpendicular

(d) $\overrightarrow A  \cdot \overrightarrow B  \leqslant 0$

Ans: Options (a) and (d)

Given that, $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$

That gives us, $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  + 0} \right|$

Hence, $\overrightarrow B  = 0$

So the option (a) is correct.

Now if $\overrightarrow A ,\overrightarrow B $ are anti-parallel, then we can write $\overrightarrow B  =  - k\overrightarrow A $

Then, we have

$ \Rightarrow \left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - k\overrightarrow A } \right|$

$ \Rightarrow \left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {1 - k} \right|\left| {\overrightarrow A } \right|$

Now $\left| {1 - k} \right|\left| {\overrightarrow A } \right|$ is not necessarily equal to $\left| {\overrightarrow A } \right|$ , hence option (b) is wrong.

Also if $\overrightarrow A ,\overrightarrow B $ are perpendicular, then we have the magnitude of the resultant vector always greater than that of the two vectors i.e. $\left| {\overrightarrow A  + \overrightarrow B } \right| > \left| {\overrightarrow A } \right|$ and $\left| {\overrightarrow A  + \overrightarrow B } \right| > \left| {\overrightarrow B } \right|$

Hence, option (c) is wrong.

Now if $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A } \right|$

Then we have

$ \Rightarrow {\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} + 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| = {\left| {\overrightarrow A } \right|^2}$

$ \Rightarrow \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| =  - \dfrac{{{{\left| {\overrightarrow B } \right|}^2}}}{2}$

Hence, $ \Rightarrow \left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right| \leqslant 0$

So option (d) is correct.

Hence, the correct answer is option (a) and (d).

MULTIPLE CHOICE QUESTIONS-II

4.11. Two particles are projected in air with speed vₒ at angles ${\theta _1}$ and ${\theta _2}$ (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than of the second, then tick the right choices

(a) angle of projection: ${\theta _1} > {\theta _2}$

(b) time of flight: T1>T2

(c) horizontal range: R1>R2

(d) total energy: U1<U2

Ans: Options (a) and (b) 

Given that, ${h_1} > {h_2}$

Hence, $\dfrac{{{v_0}^2{{\sin }^2}{\theta _1}}}{{2g}} > \dfrac{{{v_0}^2{{\sin }^2}{\theta _2}}}{{2g}}$

That gives, ${\sin ^2}{\theta _1} > {\sin ^2}{\theta _2}$

${\theta _1} > {\theta _2}$

Also, the ratio of time of flight is $\dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{2{v_0}\sin {\theta _1}/g}}{{2{v_0}\sin {\theta _2}/g}} = \dfrac{{\sin {\theta _1}}}{{\sin {\theta _2}}}$

Since $\sin {\theta _1} > \sin {\theta _2}$ hence ${T_1} > {T_2}$

And the ratio of their horizontal range is,

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{v_0}^2\sin 2{\theta _1}}}{g} \times \dfrac{g}{{{v_0}^2\sin 2{\theta _2}}}$

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{\sin 2{\theta _1}}}{{\sin 2{\theta _2}}}$

$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{2\sin {\theta _1}\cos {\theta _1}}}{{2\sin {\theta _2}\cos {\theta _2}}}$

Since ${\theta _1} > {\theta _2}$ hence ${R_1} > {R_2}$

But if ${\theta _1} + {\theta _2} = 90^\circ $ then   ${R_1} = {R_2}$

Also, the total energy of the two given particles for this motion depends on their respective masses, and since the relation between their masses is not given hence we can not determine the relation between their total energies.

Hence, the correct answers are (a) and (b).

4.12. A particle slides down a frictionless parabolic ($y = {x^2}$  ) track (A – B – C) starting from rest at point A as in figure. Point B is at the vertex of parabola and point C is at a height less than that of point A. After c, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then

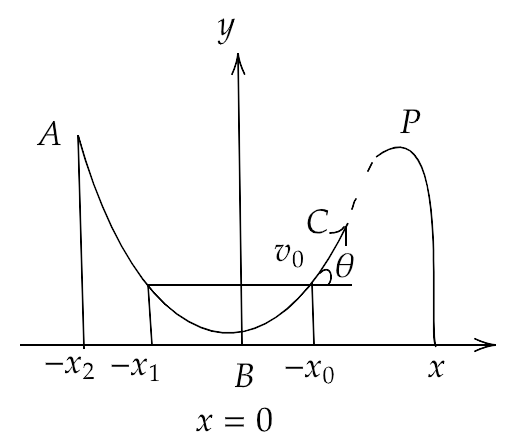
(a) KE at p= KE at B

(b) height at p = height at A

(c) total energy at p= total energy at A

(d) time of travel from A to B =time of travel from B to P.

(a) Since the kinetic energy of the particle will be maximum at the point B, hence the K.E. at point B will be greater than the K.E. at point P.

(b) Since the potential energy of the particle will be maximum at the point A, hence the height at point A will be greater than the height at point P.

(c) As the path ABC is frictionless of air and plane, therefore the total energy of the particle will remain unchanged at any point throughout the journey and is equal at the point A and P.

(d) Since the path from A to B is greater than the path from B to P, therefore the time of travel from A to B is greater than the time of travel from B to P.

4.13. Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one(s).

(a) ${\overrightarrow v _{av}} = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_1}} \right) + \overrightarrow v \left( {{t_2}} \right)} \right]$

(b) ${\overrightarrow v _{av}} = \dfrac{{\overrightarrow r \left( {{t_2}} \right) - \overrightarrow r \left( {{t_1}} \right)}}{{{t_2} - {t_1}}}$

(c) $\overrightarrow r  = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_2}} \right) - \overrightarrow v \left( {{t_1}} \right)} \right] \div \left( {{t_2} - {t_1}} \right)$

(d) ${\overrightarrow a _{av}} = \dfrac{{\overrightarrow v \left( {{t_2}} \right) - \overrightarrow v \left( {{t_1}} \right)}}{{\left( {{t_2} - {t_1}} \right)}}$

Ans: Options (a) and (c) 

The first condition ${\overrightarrow v _{av}} = \dfrac{1}{2}\left[ {\overrightarrow v \left( {{t_1}} \right) + \overrightarrow v \left( {{t_2}} \right)} \right]$ is possible if and only if the given acceleration is uniform but not otherwise.

Also, the dimensions in the third conditions are not equal in the LHS and RHS.

Therefore, the correct answers are (a) and (c).

4.14. For a particle performing uniform circular motion, choose the correct statement(s) from the following:

(a) Magnitude of particle velocity (speed) remains constant.

(b) Particle velocity remains directed perpendicular to the radius vector.

(c) Direction of acceleration keeps changing as the particle moves.

(d) Angular momentum is constant in magnitude but direction keeps changing.

Ans: Options (a), (b) and (C) 

In a uniform circular motion, the velocity is constant in the tangential direction and the direction of acceleration keeps changing at every instant of motion.

(a) Since the motion is uniform, hence the magnitude of velocity remains constant.

(b) As the direction of the velocity is tangential throughout the circular motion, so it is perpendicular to the radius vector.

(c) The acceleration of a particle moving in a uniform circular motion is always directed towards the centre. Therefore, at every point of the motion, the direction of the acceleration keeps changing in order to be directed towards the centre.

(d) Since the velocity and the radius vector remains constant in a uniform circular motion, therefore the angular momentum $\overrightarrow L  = m\left( {\overrightarrow v  \times \overrightarrow r } \right)$ also remains constant. Also the direction of the angular momentum is always constant and perpendicular towards the plane containing the velocity and radius vectors.

Hence, the correct answers are (a), (b) and (c) and option (d) is wrong.

4.15. For two vectors $\overrightarrow A $ and $\overrightarrow B $ , $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - \overrightarrow B } \right|$ is always true when

(a) $\left| {\overrightarrow A } \right| = \left| {\overrightarrow B } \right| \ne 0$

(b) $\overrightarrow A  \bot \overrightarrow B $

(c) $\left| {\overrightarrow A } \right| = \left| {\overrightarrow B } \right| \ne 0$ and $\overrightarrow A $ and $\overrightarrow B $ are parallel or anti-parallel

(d) Either $\left| {\overrightarrow A } \right|{\text{ or }}\left| {\overrightarrow B } \right|$ is zero

Given that $\left| {\overrightarrow A  + \overrightarrow B } \right| = \left| {\overrightarrow A  - \overrightarrow B } \right|$

That gives, ${\left| {\overrightarrow A  + \overrightarrow B } \right|^2} = {\left| {\overrightarrow A  - \overrightarrow B } \right|^2}$

${\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} + 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = {\left| {\overrightarrow A } \right|^2} + {\left| {\overrightarrow B } \right|^2} - 2\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta $

That is, $4\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 0$

Therefore, either $\left| {\overrightarrow A } \right|{\text{ or }}\left| {\overrightarrow B } \right|$ is zero or $\theta  = 90^\circ $ i.e. $\overrightarrow A  \bot \overrightarrow B $

VERY SHORT ANSWER TYPE QUESTIONS

4.16. A cyclist starts from centre O of a circular park of radius 1 Km and moves along the path OPRQO as shown in the figure. If he maintains the constant speed of 10m/s, what is his acceleration at point R in magnitude and direction?

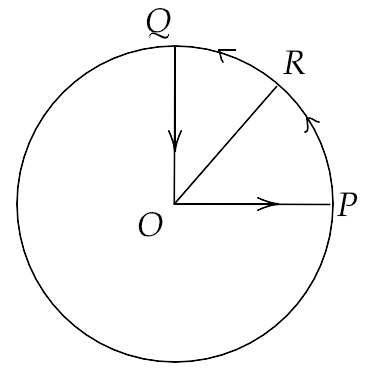
Ans: His acceleration at point R will be given by $a = \dfrac{{{v^2}}}{r}$

That gives, $a = \dfrac{{100{m^2}{s^{ - 2}}}}{{1000m}} = 0.1\,m{s^{ - 2}}$

The direction of the acceleration will be along RO.

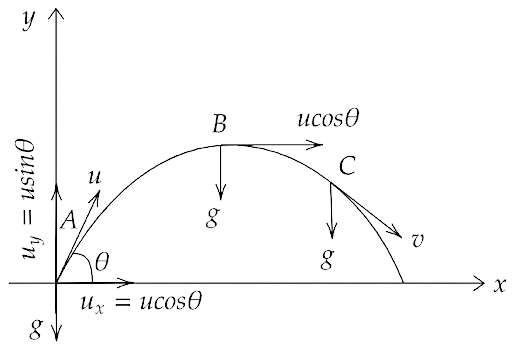
4.17. A particle is projected in the air at some angle to the horizontal, moves along the parabola as shown in the figure, where x and y indicate horizontal and vertical directions respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.

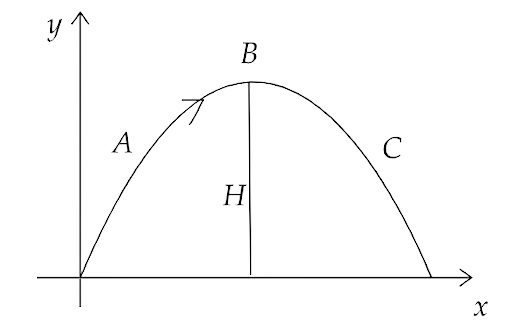
Ans: The direction of velocity is always tangential towards the direction of motion at any point of the trajectory. And since , in the given figure point B is maximum height of trajectory, hence the vertical component of B is zero and the horizontal component is $u\cos \theta $.

Also at the points A and C, gravitational acceleration $g$ is acting downwards. Hence, the direction of velocity and acceleration at points A, B and C is shown in the figure below.

4.18. A ball is thrown from a rooftop at an angle of 45⁰ above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have

(a) greatest speed

Ans: The  path of the ball can be shown by the figure given below:

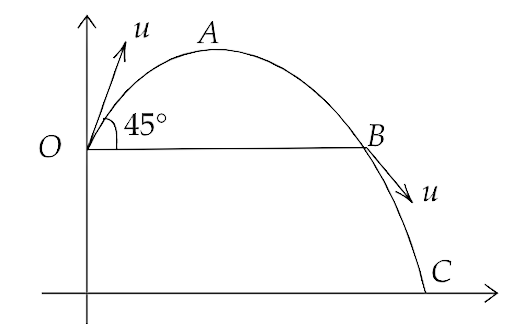
(a) The maximum speed of the ball will be at point C, given by ${v_y}$ as maximum and ${v_x} = u\cos 45^\circ  = \dfrac{u}{{\sqrt 2 }}$

(b) smallest speed

Ans: The minimum speed will be at the maximum height B where ${v_y}$ is zero and ${v_x} = \dfrac{u}{{\sqrt 2 }}$

(c) greatest acceleration? Explain.

Ans: Since the force acting on the ball is gravitational force only, hence the acceleration of the ball is always downwards and equal to $g$ .

4.19. A football is kicked into the air vertically upwards. What is its 

(a) Acceleration, and 

Ans: Since the football is kicked vertically upwards and the only acting force on the ball is the gravitational force. Hence, the acceleration at every point of trajectory of the ball is $g$ .

(b) Velocity at the Highest Point?

Ans: The velocity of the football at the highest point will be zero because both components of its velocity will be equal to zero at the highest point.

4.20. A, B and C are three non-collinear, non-co-planar vectors. What can you say about the direction of $\overrightarrow A  \times \left( {\overrightarrow B  \times \overrightarrow C } \right)$ ?

Ans: Using the right-hand thumb rule we can say that the vector $\left( {\overrightarrow B  \times \overrightarrow C } \right)$ will be perpendicular to the plane which have the vectors $\overrightarrow B $ and $\overrightarrow C $ . Then again, the direction of $\overrightarrow A  \times \left( {\overrightarrow B  \times \overrightarrow C } \right)$ will be perpendicular to $\overrightarrow A $ and in the plane containing the two vectors $\overrightarrow B $ and $\overrightarrow C $ .

SHORT ANSWER TYPE QUESTIONS

4.21. A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give an explanation to support your diagram.

Ans: Let the vertical velocity of the tossed ball be v and speed of the car be u which must be equal to the horizontal velocity of the ball.

The ball has both components of motion, hence it will have a parabolic trajectory when observed from a distance. This can be shown by the figure below.

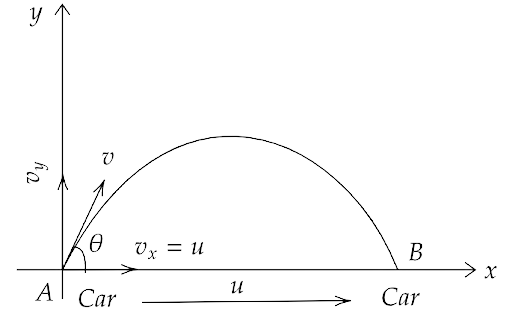
When this motion is observed by the boy sitting in the car, it will look like only a vertically up-down motion and he will catch the ball when it comes back to the ground if the car has a constant velocity.

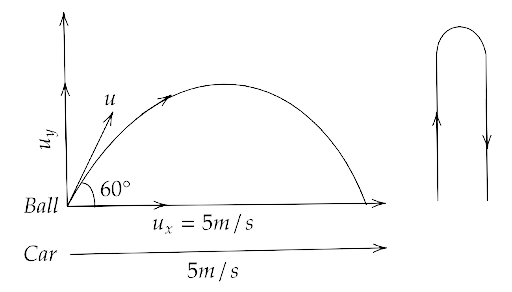
4.22. A boy throws a ball in the air at 60⁰ to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if the car has a speed of (18 km/h). Give an explanation to support your diagram.

Ans: Given that, the initial velocity of the ball $u = 10m/s$

That gives, ${u_x} = u\cos 60^\circ  = 10 \cdot \dfrac{1}{2} = 5m/s$

Velocity of car is in the direction of ${u_x}$ and equal to $18 \cdot \dfrac{5}{{18}} = 5m/s$ 

Now since they have equal horizontal velocity hence they will cover equal distances when the ball comes down. But, the ball also has a vertical velocity of ${u_y} = u\cos 30^\circ  = 10 \cdot \dfrac{{\sqrt 3 }}{2} = 5\sqrt {3m/s} $ hence it travels upwards in a parabolic trajectory.

When observed by the car, this motion will look like a simple vertical up-down motion as shown below.

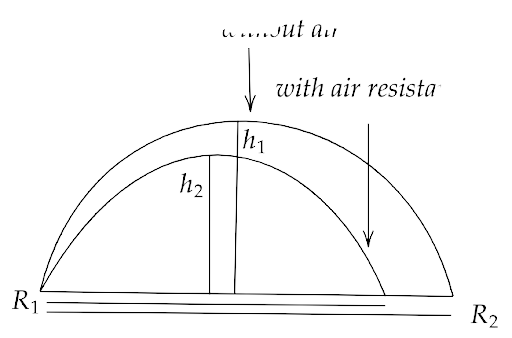
4.23. In dealing with the motion of a projectile in the air, we ignore the effect of air resistance on the motion. This gives the trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? sketch such a trajectory and explain why you have drawn it that way.

Ans: If the air resistance is included in a parabolic trajectory then both the horizontal and vertical speed of the particle will decrease due to that resistance. This will result in a decrease in the maximum attained height and in the range achieved by the particle. These two conditions can be compared by the figure drawn below:

4.24. A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At What angle of sight (w.r.t horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?

Ans: The velocity of the fighter plane at a height $h = 1.5\,km = 1500\,m$ is given as $u = 720\,km/h = 720 \cdot \dfrac{5}{{18}} = 200\,m/s$

Let the plane drops the bomb t seconds before the target is exactly below the plane.

Then in t seconds, the bomb must cover the vertical distance of 1500m under free fall with initial velocity zero.

Hence, $h = ut + \dfrac{1}{2}g{t^2}$

That gives, $1500 = 0 + \dfrac{1}{2}10{t^2}$

$t = \sqrt {300}  = 10\sqrt 3 s$

Now distance covered by the plane is $ut = 200 \times 10\sqrt 3  = 2000\sqrt 3 $

Hence, $\tan \theta  = \dfrac{{1500}}{{2000\sqrt 3 }} = \dfrac{{\sqrt 3 }}{4}$

Therefore, $\theta  = {\tan ^{ - 1}}\dfrac{{\sqrt 3 }}{4} = 23^\circ 42'$

4.25. (a) Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of the earth due to earth’s rotation (period 1 day). What is the acceleration of an object on the surface of earth (at equator) towards its center? What is it at latitude $\theta $ ? How do these accelerations compare with $g = 9.8\,m/{s^2}$ ?

Ans: The angular acceleration towards the centre in a circular motion is given by, $a = \dfrac{{{v^2}}}{R} = \dfrac{{{\omega ^2}{R^2}}}{R} = {\omega ^2}R$

Here, $\omega  = \dfrac{{2\pi }}{T}$ and $T = 24 \times 3600s$

Now the acceleration of the person on the surface of earth towards the centre of earth is given by, $a = {\omega ^2}R = {\left( {\dfrac{{2\pi }}{T}} \right)^2}R = \dfrac{{4{\pi ^2}R}}{{{T^2}}}$

That gives, $a = \dfrac{{4 \times 22 \times 22 \times 6.4 \times {{10}^6}}}{{7 \times 7 \times 24 \times 24 \times 3600 \times 3600}} = 0.034m/{s^2}$

Now at equator, i.e. latitude $\theta  = 0^\circ $

Acceleration compared with $g = 9.8m/{s^2}$ is $\dfrac{a}{g} = \dfrac{{0.034}}{{9.8}} = \dfrac{1}{{288}}$ which is a very small quantity

(b) Earth also moves in circular orbit around the sun once every year with an orbital radius of $1.5 \times {10^{11}}m$ . What is the acceleration of earth (or any object on the surface of the earth) towards the center of the sun? How does this acceleration compare with $g = 9.8m/{s^2}$ .

Ans: For the revolution of earth around the sun we have,

$R = 1.5 \times {10^{11}}m$ and $T = 365 \times 24 \times 3600 = 3.15 \times 1{0^7}s$

Since, $a = {\omega ^2}R = {\left( {\dfrac{{2\pi }}{T}} \right)^2}R = \dfrac{{4{\pi ^2}R}}{{{T^2}}}$

Hence, $a = \dfrac{{4 \times 3.14 \times 3.14 \times 1.5 \times {{10}^{11}}}}{{3.15 \times 3.15 \times {{10}^7} \times {{10}^7}}} \approx 6 \times 1{0^{ - 3}}m/{s^2}$

Comparing this acceleration with $g = 9.8m/{s^2}$ we have $\dfrac{a}{g} = \dfrac{{6 \times 1{0^{ - 3}}}}{{9.8}} = \dfrac{1}{{1633}}$

4.26. Given below in column I are the relations between vectors $\overrightarrow a ,\overrightarrow b {\text{ and }}\overrightarrow c $ and in column II are the orientations of $\overrightarrow a ,\overrightarrow b {\text{ and }}\overrightarrow c $ in the X-Y plane. Match the relation in column I to correct orientations in column II.

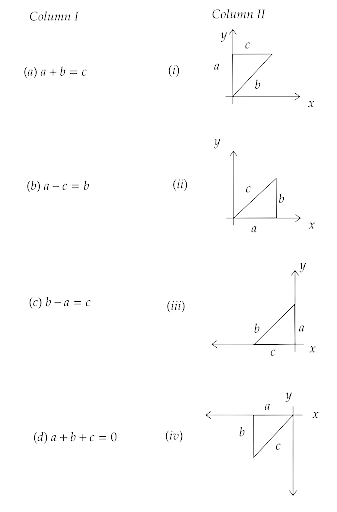
Ans: The correct match for the elements of column I and II are as follows:

4.27. If $\left| A \right| = 2$ and $\left| B \right| = 4$ , then match the relations in column I with the angle $\theta $ between A and B in column II.

Ans: (a) $\overrightarrow A  \cdot \overrightarrow B  = 0$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 0$

i.e., $\cos \theta  = 0$

Hence, $\theta  = 90^\circ $

(b) $\overrightarrow A  \cdot \overrightarrow B  =  + 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 8$

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get, $\cos \theta  = 1$

Hence, $\theta  = 0^\circ $

(c) $\overrightarrow A  \cdot \overrightarrow B  = 4$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  = 4$

Since $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\cos \theta  = \dfrac{1}{2}$

Hence, $\theta  = 60^\circ $

(d) $\overrightarrow A  \cdot \overrightarrow B  =  - 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\cos \theta  =  - 8$

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$ so we get $\cos \theta  =  - 1$

Hence, $\theta  = 180^\circ $

Hence, the correct match for the elements of column I and II are as follows:

4.28. If $\left| A \right| = 2$ and $\left| B \right| = 4$ Then match the relations in column I with the angle $\theta $ between A and B in column II.

Ans: (a) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 0$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 0$

i.e., $\sin \theta  = 0$

(b) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 8$

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 8$

Since | A | = 2 and | B| = 4, so we get, $\sin \theta  = 1$

(c) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 4$

This give us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 4$

Since $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\sin \theta  = \dfrac{1}{2}$

Hence,$\theta  = 30^\circ $

(d) $\left| {\overrightarrow A  \times \overrightarrow B } \right| = 4\sqrt 2 $

This gives us $\left| {\overrightarrow A } \right|\left| {\overrightarrow B } \right|\sin \theta  = 4\sqrt 2 $

Since, $\left| A \right| = 2$ and $\left| B \right| = 4$, so we get $\sin \theta  = \dfrac{1}{{\sqrt 2 }}$

Hence, $\theta  = 45^\circ $

LONG ANSWER TYPE QUESTIONS

4.29. A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The cannon is located at a distance of 800 m from the foot of the hill and can be moved on the ground at a speed of 2 m/s; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach the ground across the hill? Take $g = 10\,m/{s^2}$ .

Ans: We are given that the speed of packets is 125 m/s  and the height of the hill is 500 m.

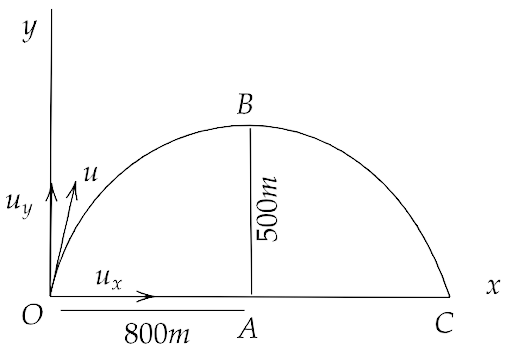
Now, in order to cross the hill by packet, the vertical components of the speed of packet must be reduced so that it can attain a height of 500 m and the distance between the hill and the cannon must be half of the range of the packet.

Hence, 

$ \Rightarrow {v^2} = {u^2} + 2gh$

$ \Rightarrow 0 = {u_y}^2 - 2gh$

That gives, $ \Rightarrow {u_y}^2 = \sqrt {2gh}  = \sqrt {2 \times 10 \times 500}  = 100m/s$

Now, we have 

$ \Rightarrow {u^2} = {u_x}^2 + {u_y}^2$

Hence, ${u_x}^2 = {125^2} - {100^2} = 25 \times 125$

i.e. ${u_x} = 5 \times 15 = 75m/s$

Now, the vertical motion of the packet is given by ${v_y} = {u_y} + gt$ i.e. $0 = 100 - 10t$ or $t = 10s$

Hence, the time of half flight and time to reach the top of the hill is 10 seconds.

Therefore the cannon must be at the half range i.e. at the horizontal distance in 10 sec

Hence the distance between the hill and the canon is given by ${u_x} \times 10 = 75 \times 10 = 750m$

Therefore the required distance for the cannon is $800 - 750 = 50m$

Time taken by the cannon to cover 50m is $\dfrac{{50}}{2} = 25s$

Therefore, the total time taken by the packet from 800 m away from the hill to reach the other side of the hill is equal to $25 + 10 + 10 = 45s$ .

4.30. A gun can fire shells with maximum speed ${v_0}$ and the maximum horizontal range that can be achieved is $R = \dfrac{{{v_0}^2}}{g}$ . If a target farther away by distance $\Delta x$ (beyond R) has to be hit with the same gun as shown in the figure here. Show that it could be achieved by raising the gun to a height at least $h = \Delta x\left[ {1 + \dfrac{{\Delta x}}{R}} \right]$

Hint: This problem can be approached in two different ways:

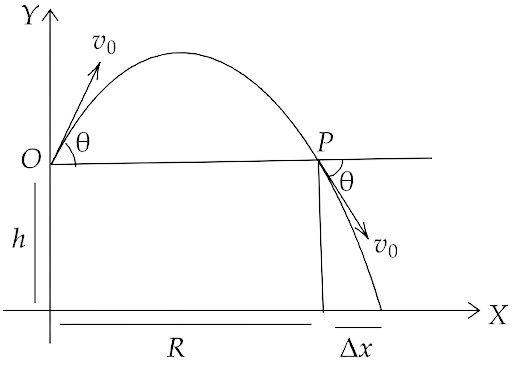
(i) Refer to the diagram: target T is at the horizontal distance $x = R + \Delta x$ and below the point of projection y=-h.

(ii) From point P in the diagram: Projection at speed ${v_0}$ at an angle $\theta $ below horizontal with height h and horizontal range $\Delta x$ .

Ans: The maximum horizontal range is given as $R = \dfrac{{{v_0}^2}}{g}$

That means the angle of projection must be $\theta  = 45^\circ $

If the gun is raised to a height h from the horizontal level of target T so that the projectile can hit the target T,

Then the total range of the projectile must be $x = R + \Delta x$

Also the horizontal component of velocity at the point A will be given by ${v_0}\cos \theta $

Now, the magnitude of velocity will be the same at the points A and P because they are on the same level, but having opposite directions.

Therefore, the horizontal and vertical velocities at P will be ${v_x} =  - {v_0}\cos \theta $ and ${v_y} = {v_0}\sin \theta $ respectively.

Now, we have $h = ut + \dfrac{1}{2}a{t^2}$

Hence, $h =  - {v_0}\sin \theta \left( t \right) + \dfrac{1}{2}g{t^2}$

Also since the AT is $R + \Delta x = {v_0}\cos \theta  \cdot t$ ,that gives $t = \dfrac{{R + \Delta x}}{{{v_0}\cos \theta }}$

Now substituting this value in the above equation, we get

$ \Rightarrow h =  - {v_0}\sin \theta \left( {\dfrac{{R + \Delta x}}{{{v_0}\cos \theta }}} \right) + \dfrac{1}{2}g{\dfrac{{\left( {R + \Delta x} \right)}}{{{v_0}^2{{\cos }^2}\theta }}^2}$

That gives, since $\theta  = 45^\circ $

$ \Rightarrow h =  - \tan \theta \left( {R + \Delta x} \right) + \dfrac{1}{2}\left( {\dfrac{g}{{{v_0}^2}}} \right){\dfrac{{\left( {R + \Delta x} \right)}}{{\dfrac{1}{2}}}^2}$

$ \Rightarrow h =  - \left( {R + \Delta x} \right) + \left( {\dfrac{g}{{{v_0}^2}}} \right){\left( {R + \Delta x} \right)^2}$

Since, $\left( {\dfrac{g}{{{v_0}^2}}} \right) = \dfrac{1}{R}$ hence

$ \Rightarrow h =  - R - \Delta x + \dfrac{1}{R}\left( {{R^2} + \Delta {x^2} + 2R\Delta x} \right)$

$ \Rightarrow h =  - R - \Delta x + R + \dfrac{{\Delta {x^2}}}{R} + 2\Delta x = \dfrac{{\Delta {x^2}}}{R} + \Delta x$

$ \Rightarrow h = \Delta x\left[ {1 + \dfrac{{\Delta x}}{R}} \right]$

4.31. A particle is projected in air at an angle $\beta $ to a surface which itself is inclined at an angle $\alpha $ to the horizontal as in figure

(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which a particle will hit the surface.)

(Hint: This problem can be solved in two different ways:

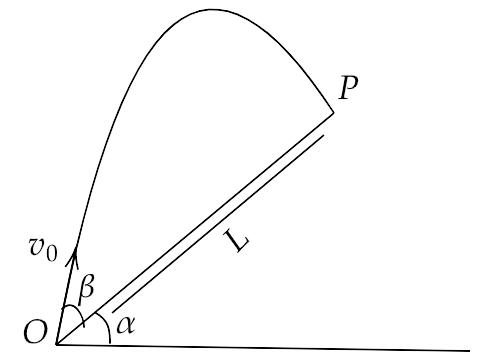
(i) Point P at which particle hits the plane can be seen as the intersection of its trajectory (parabola) and straight line. Remember a particle is projected at an angle $\left( {\alpha  + \beta } \right)$ w.r.t. horizontal.

(ii) We can take x-direction along the plane and y-direction perpendicular to the plane. In that case resolve g (acceleration due to gravity) in two different components, ${g_x}$ along the plane and ${g_y}$ perpendicular to the plane. Now the problem can be solved as two independent motions in x and y directions respectively with time as a common parameter.)

Ans: Now we find (a).

Since we have, $x = L,{u_x} = {v_0}\cos \beta ,{a_x} =  - g\sin \alpha $ and $t = T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$

Hence, $s = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$

Gives us, $L = {v_0}\cos \beta  \cdot T + \dfrac{1}{2}\left( { - g\sin \alpha } \right){T^2} = T\left[ {{v_0}\cos \beta  - \dfrac{1}{2}g\sin \alpha T} \right]$

Putting $T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$ gives us,

$ \Rightarrow L = \dfrac{{2{v_0}^2\sin \beta }}{{g{{\cos }^2}\alpha }}\cos \left( {\alpha  + \beta } \right)$

That is the required range.

(b) Time of flight.

Ans: Let us first calculate the (b) time of flight.

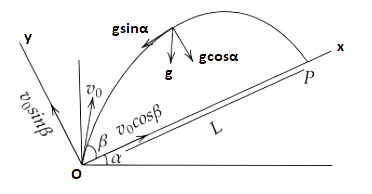
$ \Rightarrow s = ut + \dfrac{1}{2}g{t^2}$

Where, $s = 0,u = {u_y} = {v_0}\sin \beta ,g = {g_y} =  - g\cos \alpha ,t = T$

$ \Rightarrow 0 = {v_0}\sin \beta \left( T \right) + \dfrac{1}{2}\left( { - g\cos \alpha } \right){T^2}$

$ \Rightarrow T\left[ {{v_0}\sin \beta  - T\dfrac{g}{2}\cos \alpha } \right] = 0$

So either T is zero or ${v_0}\sin \beta  - T\dfrac{g}{2}\cos \alpha $

That gives the time of flight as $T = \dfrac{{2{v_0}\sin \beta }}{{g\cos \alpha }}$

(c) $\beta $ at Which range will be maximum.

Ans: Let us consider the equation $Z = \sin \beta \cos \left( {\alpha  + \beta } \right)$

We can write $Z = \sin \beta \cos \left( {\alpha  + \beta } \right) = \dfrac{1}{2}\left[ {\sin \left( {2\beta  + \alpha } \right) - \sin \alpha } \right]$

Now for Z to be maximum, it must have  $\sin \left( {2\beta  + \alpha } \right) = 1$ i.e. $\sin \left( {2\beta  + \alpha } \right) = \sin 90^\circ $

That gives, $2\beta  + \alpha  = 90^\circ $

Hence, $\beta  = \dfrac{{90^\circ  - \alpha }}{2}$ or $\beta  = \dfrac{\pi }{4} - \dfrac{\alpha }{2}$

4.32. A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle with speed ${v_0}$ and rebounds elastically as shown in the figure. Find the distance along the plane where it will hit the second time.

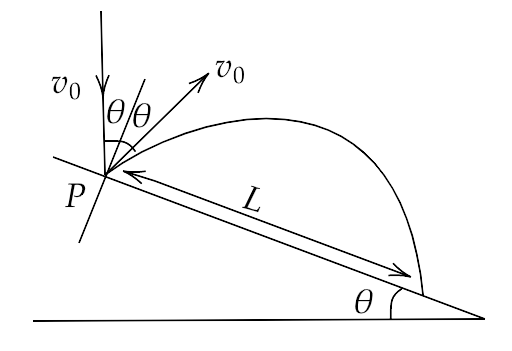
(Hint: (i) After rebound, the particle still has speed ${v_0}$ to start.

(ii) Work out angle particle speed is horizontal after it rebounds.

(iii) Rest is similar to if a particle is projected up the incline.)

Ans: Considering the motion of particle from the point O to the point A along y-axis, we can write

$ \Rightarrow {s_y} = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$

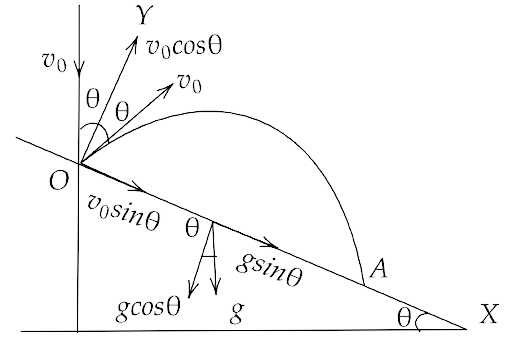
Where we have ${s_y} = 0,{u_y} = {v_0}\cos \theta ,t = T,{a_y} =  - g\cos \theta $

$ \Rightarrow 0 = {v_0}\cos \theta  \cdot T - \dfrac{1}{2}g\cos \theta {T^2}$

$ \Rightarrow T\left[ {{v_0}\cos \theta  - \dfrac{1}{2}g\cos \theta T} \right] = 0$

Now since T can not be zero hence ${v_0}\cos \theta  = \dfrac{1}{2}g\cos \theta T$

That gives $\dfrac{{2{v_0}}}{g} = T$

Now, considering the motion along x-axis we have,

$ \Rightarrow {s_x} = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$

$ \Rightarrow L = \left( {\dfrac{{2{v_0}}}{g}} \right){v_0}\sin \theta  + \dfrac{1}{2}g\sin \theta {\left( {\dfrac{{2{v_0}}}{g}} \right)^2}$

$ \Rightarrow L = \dfrac{{2{v_0}^2\sin \theta }}{g} + \dfrac{{2{v_0}^2\sin \theta }}{g}$

$ \Rightarrow L = \dfrac{{4{v_0}^2}}{g}\sin \theta $

4.33. A girl riding a bicycle with a speed of 5 m/s towards the north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground-based observer?

(Hint: Assume north to be $\widehat i$ direction and vertically downward to be $ - \widehat j$ . Let the rain velocity ${v_r}{\text{ be }}a\widehat i + b\widehat j$ . The velocity of rain as observed by the girl is always ${v_r} - {v_{girl}}$ . Draw the vector diagram/s for the information given and find a and b. You may draw all vectors in the reference frame of the ground-based observer.)

Ans: Let us consider the north direction as $\widehat i$ and the downward direction as $ - \widehat j$ respectively.

Consider the velocity of rain to be ${\overrightarrow v _R} = a\widehat i + b\widehat j$

Now if the speed of the girl is ${\overrightarrow v _g} = 5\widehat i$

Then the velocity of rain w.r.t. the girl will be ${\overrightarrow v _{Rg}} = \left( {a\widehat i + b\widehat j} \right) - 5\widehat i$

Now the direction of the rain is vertically downward, hence the horizontal component of ${\overrightarrow v _{Rg}}$ will be zero.

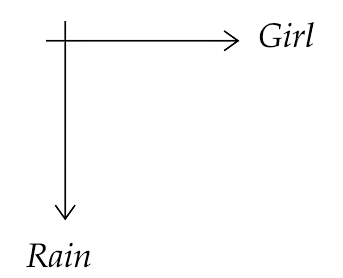
That gives us, $a\widehat i - 5\widehat i = 0$ or $a = 5$

Now if ${\overrightarrow v _g} = 10\widehat i$ and we have ${\overrightarrow v _R} = 5\widehat i + b\widehat j$

And ${\overrightarrow v _{Rg}} = \left( {5\widehat i + b\widehat j} \right) - 10\widehat i =  - 5\widehat i + b\widehat j$

Now rains appears at 45° to the vertical $\widehat j$ ,

Therefore, $\tan 45^\circ  = \dfrac{b}{a} \Rightarrow b = a$

Hence, $b =  - 5$

That gives ${\overrightarrow v _R} = 5\widehat i - 5\widehat j$

Now, $\left| {{{\overrightarrow v }_R}} \right| = \sqrt {{5^2} + {{\left( { - 5} \right)}^2}}  = \sqrt {50}  = 5\sqrt 2 m/s$

4.34. A river is flowing due east with a speed of 3m/s. A swimmer can swim in still water at a speed of 4 m/s as shown in the figure.

(a) If a swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?

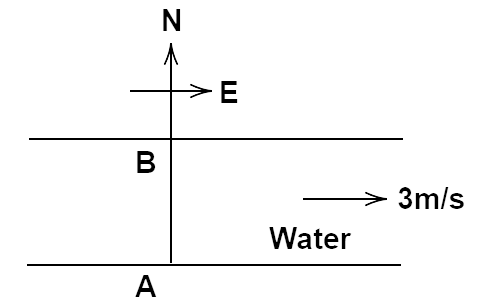
Ans: Given that, velocity towards AB and east are ${v_s} = 4m/s$ and ${v_R} = 3m/s$ respectively.

(a) Since the above given two velocities are perpendicular therefore,

We can write ${v^2} = v_s^2 + v_R^2 = 25 \Rightarrow v = 5m/s$

Also, $\tan \theta  = \dfrac{{{v_R}}}{{{v_s}}} = \dfrac{3}{4} = 0.75 \Rightarrow \theta  = {\tan ^{ - 1}}0.75 = 36^\circ 54'$

Hence $\theta $ is making $36^\circ 54$ with a north direction.

(b) If he wants to start from point A on the south bank and reaches the opposite point B on the north bank,

(i) which direction should he swim?

(ii) what will be his resultant speed?

Ans: If the swimmer strikes to swim with angle $\theta $ with north direction towards West,

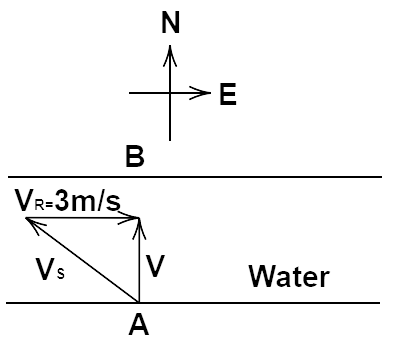
Then from figure we have, ${v^2} = v_s^2 - v_R^2 = 7 \Rightarrow v = \sqrt 7 m/s$

Hence $\theta $ is made  between the north and west direction.

(c) From two different cases as mentioned in (a) and (b)above, in which case will he reach the opposite bank in a shorter time?

Ans: Here, the component of velocity perpendicular to the river is 4 m/s.

Let the width of the river be ${d_R}$.

Time taken by the swimmer when he strikes towards North will be ${t_1} = \dfrac{{{d_R}}}{4}$

Also, time taken in part (b) will be ${t_2} = \dfrac{{{d_R}}}{{\sqrt 7 }}$

Therefore, the ratio of both time taken is given by 

$ \Rightarrow \dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{{d_R}}}{4} \times \dfrac{{\sqrt 7 }}{{{d_R}}} = \dfrac{{\sqrt 7 }}{4}$

That gives us the relation ${t_2} > {t_1}$.

Hence, the swimmer will reach the opposite bank in a shorter time in the case (a).

4.35. A cricket fielder can throw the cricket ball with a speed ${v_0}$ . If he throws the ball while running with speed u at an angle $\theta $ to the horizontal, find

(a) the effective angle to the horizontal at which the ball is projected in the air as seen by a spectator.

Ans: (a) Given that, a cricket fielder runs with velocity u in the horizontal direction and he throws the ball while running.

Therefore the horizontal component of the ball also includes his own speed u.

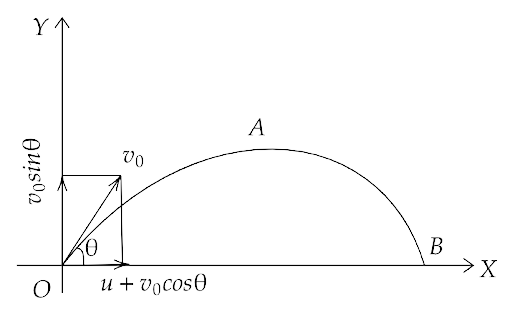
Hence, ${u_x} = u + {v_0}\cos \theta $

The fielder runs horizontally, hence the vertical component of velocity of the ball is not affected.

That gives, ${u_y} = {v_0}\sin \theta $

Also, we have $\tan \theta  = \dfrac{{{u_y}}}{{{u_x}}} = \dfrac{{{v_0}\sin \theta }}{{u + {v_0}\cos \theta }}$

Therefore, $\theta  = {\tan ^{ - 1}}\dfrac{{{v_0}\sin \theta }}{{u + {v_0}\cos \theta }}$

(b) what will be the time of flight?

Ans: Since we have, ${s_y} = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$

Where ${s_y} = 0,{u_y} = {v_0}\sin \theta ,{a_y} =  - g,t = T$

Therefore, we get $0 = {v_0}\sin \theta \left( T \right) - \dfrac{1}{2}g{T^2}$

Or, $T\left[ {{v_0}\sin \theta  - \dfrac{1}{2}gT} \right] = 0$

Since T cannot be zero, therefore ${v_0}\sin \theta  = \dfrac{1}{2}gT$

That gives, $T = \dfrac{{2{v_0}\sin \theta }}{g}$

(c) what is the distance (horizontal range) from the point of projection at which the ball will land?

Ans: For the range to be maximum, we have $\dfrac{{dR}}{{d\theta }} = 0$

Therefore, $\dfrac{{d\dfrac{{{v_0}}}{g}\left[ {2u\sin \theta  + {v_0}\sin 2\theta } \right]}}{{d\theta }} = 0$

That gives, $\dfrac{{{v_0}}}{g}\left[ {2u\cos \theta  + 2{v_0}\cos \theta } \right] = 0$

(d) find θ at which he should throw the ball that would maximise the horizontal range as found in (c).

Ans: Now since $\dfrac{{{v_0}}}{g} \ne 0$ hence $2u\cos \theta  + 2{v_0}\cos \theta  = 0$

That gives, $2{v_0}{\cos ^2}\theta  + u\cos \theta  - {v_0} = 0$

Using quadratic formula we get, $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}}$

Hence, $\theta  = {\cos ^{ - 1}}\left( {\dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}}} \right)$

(e) how does θ for maximum range change if $u > {v_0},u = {v_0},u < {v_0}$

Ans: If we have $u = {v_0}$

Then $\cos \theta  = \dfrac{{ - {v_0} \pm \sqrt {{v_0}^2 + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - 1 \pm 3}}{2}$

Taking positive sign, $\cos \theta  = \dfrac{{ - 1 + 3}}{2} = \dfrac{1}{2}$

Hence, $\theta  = {\cos ^{ - 1}}\dfrac{1}{2} = 60^\circ $

Now, if $u <  < {v_0}$ then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - u \pm 2\sqrt 2 {v_0}}}{{4{v_0}}}$

Taking positive sign, $\cos \theta  = \dfrac{{2\sqrt 2 {v_0}}}{{4{v_0}}} = \dfrac{1}{{\sqrt 2 }}$

Hence, $\theta  = {\cos ^{ - 1}}\dfrac{1}{{\sqrt 2 }} = 45^\circ $

Also, if $u >  > {v_0}$ then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ - u \pm u}}{{4{v_0}}}$

Taking positive sign, $\cos \theta  = \dfrac{{ - u + u}}{{4{v_0}}} = 0$

Hence, $\theta  = {\cos ^{ - 1}}0 = 90^\circ $

(f) how does θ in (v) compare with that for u = 0 (i.e. 45⁰)?

Ans: If we have $u = 0$

Then we have $\cos \theta  = \dfrac{{ - u \pm \sqrt {{u^2} + 8{v_0}^2} }}{{4{v_0}}} = \dfrac{{ \pm 2\sqrt 2 {v_0}}}{{4{v_0}}}$

4.36. Motion in two dimensions in a plane can be studied by expressing position, velocity and acceleration as vectors in Cartesian co-ordinates $\overrightarrow A  = {A_x}\widehat i + {A_y}\widehat j$ where $\widehat i,\widehat j$ are unit vector along x and y directions, respectively and ${A_x}{\text{ and }}{A_y}$ are corresponding components of $\overrightarrow A $  (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates $\overrightarrow A  = {A_r}\widehat r + {A_\theta }\widehat \theta $ where $\widehat r = \dfrac{{\overrightarrow r }}{{\left| r \right|}} = \cos \theta \widehat i + \sin \theta \widehat j$ and $\widehat \theta  =  - \sin \theta \widehat i + \cos \theta \widehat j$ are unit vectors along direction in which ‘r’ and ‘θ ’ are increasing.

(a) Express $\widehat i$ and $\widehat j$ in terms of $\widehat r$ and $\widehat \theta $.

Ans: Given that, $\widehat r = \cos \theta \widehat i + \sin \theta \widehat j$ ...(1)

and $\widehat \theta  =  - \sin \theta \widehat i + \cos \theta \widehat j$  ...(2)

Multiplying them with $\sin \theta {\text{ and cos}}\theta $ respectively and adding

We get, $\widehat r\sin \theta  + \widehat \theta \cos \theta  = \widehat j$

Now, multiplying the first two equations with ${\text{cos}}\theta {\text{ and }}\sin \theta $ respectively and subtracting,

We get, $\widehat r\cos \theta  - \widehat \theta \sin \theta  = \widehat i$

These are the required relation of $\widehat i$ and $\widehat j$ in terms of $\widehat r$ and $\widehat \theta $.

(b) Show that both $\widehat r$ and $\widehat \theta $ are unit vectors and are perpendicular to each other.

Ans: Multiplying (1) and (2),

We get, $\widehat r \cdot \widehat \theta  = \left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)\left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)$

Or, $\left| {\widehat r} \right| \cdot \left| {\widehat \theta } \right|\cos \theta  = 0$

Now since $\left| {\widehat r} \right|{\text{ and }}\left| {\widehat \theta } \right|$ can't be zero, therefore $\cos \theta  = 0 = \cos 90^\circ $

Therefore, the angle between $\widehat r$ and $\widehat \theta $ is $90^\circ $ .

(c) Show that $\dfrac{d}{{dt}}\widehat r = \omega \widehat \theta {\text{ where }}\omega  = \dfrac{{d\theta }}{{dt}}{\text{ and }}\dfrac{{d\widehat \theta }}{{dt}} =  - \omega \widehat r$

Ans: Since $\widehat r = \cos \theta \widehat i + \sin \theta \widehat j$

Therefore, $\dfrac{{d\widehat r}}{{dt}} = \dfrac{d}{{dt}}\left( {\cos \theta \widehat i + \sin \theta \widehat j} \right) =  - \sin \theta \dfrac{{d\theta }}{{dt}}\widehat i + \cos \theta \dfrac{{d\theta }}{{dt}}\widehat j$

Or, $\dfrac{{d\widehat r}}{{dt}} = \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)\dfrac{{d\theta }}{{dt}} = \omega \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right) = \omega \widehat \theta $

Hence, $\dfrac{{d\widehat r}}{{dt}} = \omega \widehat \theta $

(d) For a particle moving along a spiral given by $\overrightarrow r  = \left| {\widehat a} \right|\left| {\widehat \theta } \right|\widehat r$ where a =1 (unit), find dimensions of ‘a’.

Ans: Given that $\overrightarrow r  = \left| {\widehat a} \right|\left| {\widehat \theta } \right|\widehat r$ 

Hence, their dimensions would be given by $\left[ {\widehat a} \right] = \dfrac{{\left[ {\overrightarrow r } \right]}}{{\left[ {\widehat \theta } \right]\left[ {\widehat r} \right]}}$

That gives us, $\left[ {\widehat a} \right] = \dfrac{{\left[ {{M^0}{L^1}{T^0}} \right]}}{{\left[ {{M^0}{L^0}{T^0}} \right]\left[ {{M^0}{L^0}{T^0}} \right]}} = \left[ {{M^0}{L^1}{T^0}} \right]$

Hence, $\left[ {\widehat a} \right] = \left[ {{M^0}{L^1}{T^0}} \right]$ , $\left[ {\widehat \theta } \right] = \left[ {{M^0}{L^0}{T^0}} \right]$ and $\left[ {\overrightarrow r } \right] = \left[ {{M^0}{L^0}{T^0}} \right]$

(e) Find velocity and acceleration in polar vector representation for particles moving along the spiral described in (d) above.

Ans: Given that $a = 1$ and $\overrightarrow r  = \widehat \theta \widehat r = \theta \left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)$

Therefore, $v = \dfrac{{d\overrightarrow r }}{{dt}} = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \dfrac{{d\widehat r}}{{dt}} = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \dfrac{d}{{dt}}\left( {\cos \theta \widehat i + \sin \theta \widehat j} \right)$

$v = \dfrac{{d\theta }}{{dt}}\widehat r + \theta \left( { - \sin \theta \widehat i + \cos \theta \widehat j} \right)\dfrac{{d\theta }}{{dt}}$

Hence, $v = \omega \widehat r + \theta \widehat \theta \omega $

Now, $\overrightarrow a  = \dfrac{{dv}}{{dt}} = \dfrac{d}{{dt}}\left[ {\omega \widehat r + \theta \widehat \theta \omega } \right] = \dfrac{d}{{dt}}\left( {\dfrac{{d\theta }}{{dt}}\widehat r + \theta \widehat \theta \dfrac{{d\theta }}{{dt}}} \right)$

Solving above equation further,

Gives us, $\overrightarrow a  = \dfrac{{{d^2}\theta }}{{d{t^2}}}\widehat r + {\omega ^2}\widehat \theta  + \dfrac{{{d^2}\theta }}{{d{t^2}}}\left( {\theta \widehat \theta } \right) + {\omega ^2}\widehat \theta  + {\omega ^2}\left( { - \widehat r} \right)$

Hence, $\overrightarrow a  = \left( {\dfrac{{{d^2}\theta }}{{d{t^2}}} - {\omega ^2}\theta } \right)\widehat r + \left( {2{\omega ^2} + \dfrac{{{d^2}\theta }}{{d{t^2}}}\theta } \right)\widehat \theta $

4.37. A man wants to reach from A to the opposite corner of the square C (as in figure). The sides of the square are 100 m. A central square of 50m × 50m is filled with sand. Outside this square, he can walk at a speed of 1 m/s. In the central square, he can walk only at a speed of $v{\text{ }}m/s\left( {v < 1} \right)$ . What is the smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?

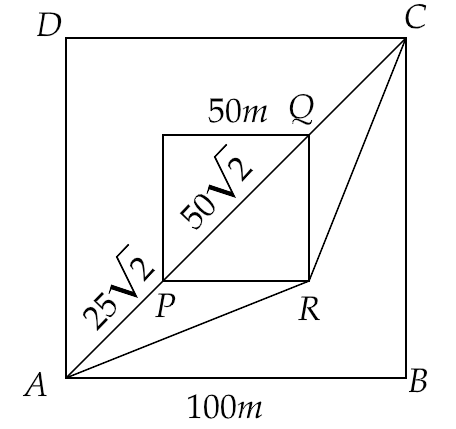
Ans: From the figure , we can obtain distance PQ by Pythagoras theorem,

Hence $PQ = \sqrt {{{50}^2} + {{50}^2}}  = 50\sqrt 2 $

Similarly, we have $AC = \sqrt {{{100}^2} + 10{0^2}}  = 100\sqrt 2 $

Total time taken in crossing the path APQC is given by,

$ \Rightarrow {t_1} = \dfrac{{\left( {AP + QC} \right)}}{{1m/s}} + \dfrac{{PQ}}{v}$

$ \Rightarrow {t_1} = \dfrac{{100\sqrt 2  - 50\sqrt 2 }}{1} + \dfrac{{50\sqrt 2 }}{v}$

$ \Rightarrow {t_1} = \dfrac{{50\sqrt 2 }}{1} + \dfrac{{50\sqrt 2 }}{v} = 50\sqrt 2 \left( {1 + \dfrac{1}{v}} \right)$

If O is the midpoint of PQ, then

Total time taken in crossing the path ARC is given by,

$ \Rightarrow {t_2} = \dfrac{{\left( {AR + RC} \right)}}{{1m/s}} = 2AR$

$ \Rightarrow AR = \sqrt {{{\left( {50\sqrt 2 } \right)}^2} + {{\left( {25\sqrt 2 } \right)}^2}}  = \left( {25\sqrt 2 } \right)\sqrt 5  = 25\sqrt {10} s$

$ \Rightarrow {t_2} = 2AR = 50\sqrt {10} s$

Now we have ${t_1} < {t_2}$

Hence, $50\sqrt 2 \left( {1 + \dfrac{1}{v}} \right) < 50\sqrt {10} $

$\left( {1 + \dfrac{1}{v}} \right) < \sqrt 5 $

That gives $\dfrac{1}{v} < \sqrt 5  - 1$

Hence, $v > \dfrac{1}{{\sqrt 5  - 1}} = \dfrac{{\sqrt 5  + 1}}{4} = \dfrac{{3.23}}{4} = 0.81$

Therefore, $v > 0.81s$.

Chapter Description

Motion in a plane is the fourth chapter of the NCERT class XI physics book part 1. After learning the concepts of motion of objects in a straight line, this chapter introduces us to the motion of objects in two directions, that is to say in a two-dimensional plane. The concept of vector and scalar values will be the first thing to be cleared in this chapter in section 4.2 ‘Scalars and Vectors.’. To make the exact measurement of the velocity and acceleration of a moving object we have to take the directions of movement into consideration. When we value physical quantities based on the directions with respect to a reference point then these are termed as vector quantities. 

It can't be wrong to say that vector quantities, except time, are the fundamental quantities involved in the expression of any other quantity. So this chapter has a very foundational character in the study of physics as a subject for quantification of laws of the natural world. In the sub-sections 4.2.1 ‘Position and Displacement Vectors,’ we will understand the nature of vectors. We will also get to know their arithmetic operations in 4.3 ‘Multiplication of Vectors by Real Numbers’ and 4.4 ‘Addition and Subtraction of Vectors’. Arithmetic operations have been established by both graphical and analytical methods. 

Various physical quantities mentioned in the previous chapter for example Velocity, acceleration, relative velocity have been explained with respect to a plane such as 'Motion in a plane with constant acceleration,' 'relative velocity in two dimensions,' etc. The most interesting of all is the 'Projectile motion' made by a moving object under the influence of gravity. All the variables of a horizontal projectile motion such as the range, maximum height obtained by the object, and time taken to achieve it have been clearly derived and established. Finally comes the concept of the ‘Uniform circular motion’ of an object. It is the motion of an object in a two-dimensional path by completing its circular  path of motion around a common point of reference called the ‘center.’

It is also important to bear in mind that the Exercises provided at the end of the chapter are as Important as the topic. so make sure that you complete all the questions provided in the chapter.  you can also refer to the solutions provided by vedantu.com. It has been prepared by very competent teachers and experts in their fields. You can get the solution in PDF format from this website.

FAQs on NCERT Exemplar for Class 11 Physics Chapter 4 - Motion in a Plane (Book Solutions)

1. Where can I get the NCERT textbook for Class XI of Physics part I?

You can easily get the NCERT textbooks by downloading it from various sources over the internet. Epathsala.nic.in is an excellent website for the same.  You can also use the app of e pathshala by downloading it from the google play store. You can also obtain the NCERT book hard copies from online shopping sites. NCERT itself also provides you with a soft copy of all the books on its website www.ncert.nic.in without any charges and registration to do so.

2. What are the basic concepts I need to know before reading this chapter?

Because the scalar and vector are the introductory concepts in class XI so you can start learning this chapter ‘motion in a plane’ without having prior knowledge of any of it. However, it is always a better way to have a hint before you start reading. The science textbook of class IX can come in handy in this situation. The chapter ‘motion’ also includes the concept of ‘circular motion.’ Some chapters of geometry in maths can be of great help to you for understanding planes and their coordinates that help to determine the position of the vectors. 

3. How much time do I need to complete this chapter?

Though you can complete reading the chapter in a single sitting for two to three hours but interpreting the concepts and fully understanding them needs more time. You also have to complete the exercises provided at the end of the chapter which surely requires more effort and time. To help you we have provided the solution of the same solved by our expert teachers at vedantu.com. You can download them from this website and refer to them when you find any difficulty while solving the equations.

4. How can I solve the problems in the exercise of the chapter?

The problem questions mentioned in the exercise section of the chapter are very necessary for the CBSE exams as well as for various competitive exams. So you must complete all the questions by yourself and then refer to the solutions provided on this page. You can also download the same for any future reference. Vedantu also helps you in solving all the exercises by making available to you all the best materials and teachers on a single website of ours.

5. Do I need the help of Vedantu NCERT Class 11 physics chapter 4 - Motion in a Plane Book solutions?

The solutions provided by the Vedantu for every chapter of the textbook have been solved by very able teachers to make you understand the application of formulas in easy steps. So it will be a great advantage for you to download the Book solutions and use it at your best. You can always solve the questions by yourself before checking out the solutions. Solutions should always be your guide to learn the process and steps for solving the questions but never duplicate the answers.

• NCERT Solutions
• NCERT Class 11
• NCERT 11 Physics
• Chapter 4: Motion In A Plane

NCERT Solutions for Class 11 Physics Chapter 4 Motion in A Plane

Ncert solutions class 11 physics chapter 4 – free pdf download.

* According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 3.

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane is one of the important study materials for Class 11 students as it is one of the most scoring chapters in kinematics. Students must try to understand each and every topic in a detailed way so that they can write appropriate answers in their examinations. To score good marks in the Class 11 examination, one must solve the questions provided at the end of each chapter in the NCERT book. Using the NCERT Solutions available at BYJU’S, students will be able to frame relevant answers based on the marking scheme of the CBSE Syllabus for 2023-24 and its guidelines.

In the last chapter, we had learnt about the concepts of displacement, position, acceleration and velocity, which are important in explaining the motion of an object in a straight line. The direction aspect can be taken care of by using the ‘+’ and ‘-‘ signs. But to explain the motion of an object in two or three dimensions, vectors can be used. To understand the basic concepts from this chapter, students can refer to NCERT Solutions for Class 11 Physics by clicking on the link provided below.

carouselExampleControls112

Previous Next

Access answers of NCERT Solutions for Class 11 Physics Chapter 4 – Motion in a Plane

Q-1: State whether the following physical quantities are scalar or vector.                    

(ii) Volume

(iii) Speed

(iv) Acceleration

(v) Density

(vi) Number of moles

(vii) Velocity

(viii) Angular frequency

(ix) Displacement

(x) Angular velocity

Scalar: Density, mass, speed, volume, angular frequency, number of moles.

Vector: Velocity, acceleration, angular velocity, displacement.

A scalar quantity depends only on the magnitude, and it is independent of the direction. Density, mass, speed, volume, angular frequency and number of moles are scalar quantities.

A vector quantity depends on the magnitude as well as the direction. Velocity, acceleration, angular velocity, and displacement comes under this.

Q-2: From the following, pick any two scalar quantities:

Force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.

The dot product of force and displacement is the work done. Work is a scalar quantity since the dot product of two quantities is always scalar.

Current is a scalar quantity as it is described only by its magnitude, and it is independent of direction.

Q-3: From the following, identify the vector quantities:

Pressure, temperature, energy, time, gravitational potential, power, total path length, charge, coefficient of friction, impulse.

Impulse is the product of force and time. Since force is a vector quantity, its product with time which is a scalar quantity, gives a vector quantity.

Q-4: State with reasons whether the following algebraic operations with scalar and vector physical quantities are meaningful :

(a) Addition of any two scalars

(b) Adding a scalar to a vector which has the same dimensions

(c) Multiplying a vector by any scalar

(d) Multiplying any two scalars

(e) Adding any two vectors

(f) Addition of a vector component to the same vector

(a) Meaningful:

The addition of two scalar quantities is meaningful only if they both represent the same physical quantity.

(b) Not Meaningful:

The addition of a vector quantity with a scalar quantity is not meaningful

(c) Meaningful:

A scalar can be multiplied with a vector. For example, force is multiplied by time to give an impulse.

(d) Meaningful:

A scalar, irrespective of the physical quantity it represents, can be multiplied by another scalar having the same or different dimensions.

(e) Meaningful:

The addition of two vector quantities is meaningful only if they both represent the same physical quantity.

(f) Meaningful:

A component of a vector can be added to the same vector as they both have the same dimensions.

Q-5: Read each statement below carefully and state with reasons if it is true or false:

(a) The magnitude of a vector is always a scalar

(b) Each component of a vector is always a scalar

(c) The total path length is always equal to the magnitude of the displacement vector of a particle

(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of the average velocity of the particle over the same interval of time

(e) Three vectors not lying in a plane can never add up to give a null vector

The magnitude of a vector is a number. So, it is a scalar.

Each component of a vector is also a vector.

The total path length is a scalar quantity, whereas displacement is a vector quantity. Hence, the total path length is always greater than the magnitude of displacement. It becomes equal to the magnitude of displacement only when a particle is moving in a straight line.

It is because of the fact that the total path length is always greater than or equal to the magnitude of displacement of a particle.

Three vectors, which do not lie in a plane, cannot be represented by the sides of a triangle taken in the same order.

Q-6: Establish the following vector inequalities geometrically or otherwise:

(a) \(\begin{array}{l}\left | a + b \right |\leq \left | a \right | + \left | b \right |\end{array} \)

(b) \(\begin{array}{l}|a-b|\geq||a|-|b||\end{array} \)

(c) \(\begin{array}{l}\left | a – b \right |\leq \left | a \right | + \left | b \right |\end{array} \)

(d) \(\begin{array}{l}| a – b |\geq | | a | – | b | |\end{array} \)

When does the equality sign above apply?

(a) Let two vectors \(\begin{array}{l}\vec{a}\end{array} \) and \(\begin{array}{l}\vec{b}\end{array} \) be represented by the adjacent sides of a parallelogram PQRS, as given in the figure.

Each side in a triangle is smaller than the sum of the other two sides.

Therefore, in \(\begin{array}{l}\Delta QRS\end{array} \) ,

QS < (QR + RS)

If the two vectors \(\begin{array}{l}\vec{a}\end{array} \) and \(\begin{array}{l}\vec{b}\end{array} \)   act along a straight line in the same direction, then:

Combine equations (iv) and (v),

(b) Let two vectors \(\begin{array}{l}\vec{a}\end{array} \) and \(\begin{array}{l}\vec{b}\end{array} \) be represented by the adjacent sides of a parallelogram PQRS, as given in the figure.

QS + RS > QR

QS + QR > RS

Combine equations (iv) and (v):

(c) Let two vectors \(\begin{array}{l}\vec{a}\end{array} \) and \(\begin{array}{l}\vec{b}\end{array} \) be represented by the adjacent sides of a parallelogram PQRS, as given in the figure.

Therefore, in \(\begin{array}{l}\Delta PSR\end{array} \) ,

PR < PS + SR

If the two vectors act along a straight line in the opposite direction, then

Combine (iii) and (iv),

(d) Let two vectors \(\begin{array}{l}\vec{a}\end{array} \) and \(\begin{array}{l}\vec{b}\end{array} \) be represented by the adjacent sides of a parallelogram PQRS, as given in the figure.

PR + SR > PS —– (i) PR > PS – SR —– (ii)

The quantity on the left-hand side is always positive, and that on the right-hand side can be positive or negative.

We take modulus on both sides to make both quantities positive:

Combine (iv) and (v):

Q-7: Given that l + m + n + o = 0, which of the given statements are true:

(a) l, m, n and o each must be a null vector.

(b) The magnitude of (l + n) equals the magnitude of (m+ o).

(c) The magnitude of l can never be greater than the sum of the magnitudes of m, n and o.

(d) m + n must lie in the plane of l and o if l and o are not collinear, and in the line of l and o, if they are collinear?

In order to make l + m + n + o = 0, it is not necessary to have all the four given vectors to be null vectors. There are other combinations which can give the sum zero.

l + m + n + o = 0

l + n = – (m + o)

Taking mode on both the sides,

Therefore, the magnitude of (l + n) is the same as the magnitude of (m + o).

l = (m + n + o)

Equation (i) shows the magnitude of l is equal to or less than the sum of the magnitudes of m, n and o.

The resultant sum of the three vectors l, (m + n), and o can be zero only if (m + n) lie in a plane containing l and o, assuming that these three vectors are represented by the three sides of a triangle.

If l and o are collinear, then it implies that the vector (m + n) is in the line of l and o. This implication holds only then the vector sum of all the vectors will be zero.  

Q-8: Three girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in Fig. 4.20. What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of path skate?

The distance between the initial and the final position of the particle is called displacement. All three girls reach from the point P to Q. The diameter of the ground is the magnitude of displacement.

Radius = 200 m

Diameter = 200 x 2 = 400 m

Hence, the magnitude of displacement is 400 m for each girl. This magnitude is equal to the path skated by girl B.

Q-9: A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes 10 min, what is the

(i) Net displacement

(ii) Average velocity and

(iii) The average speed of the cyclist

(i) The distance between the initial and final position of the body is called displacement.  The cyclist comes back to the place where he had started in 20 minutes. So, the displacement is zero.

As the displacement is zero, the average velocity is zero.

(iii) Average speed = distance travelled/time taken

= OP + Distance PQ + QO/ 10 minutes

= {1 km + (1/4) x 2 x (22/7) x 1km + 1m}/ (10/60) h

= 6 (2 + 22/14)

= 6 (50/14) = 21.43 km/h

Q-10: On an open ground, a motorist follows a track that turns to his left by an angle of 60 0 after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case

The path followed by the motorist is a regular hexagon with a side 500 m, as given in the figure.

Let the motorist start from point P.

The motorist takes the third turn at S .

The magnitude of the displacement = PS = PV + VS

= 500 + 500 = 1000 m

Total path length = PQ + QR + RS

= 500 + 500 + 500 = 1500 m

The motorist takes the 6 th turn at point P, which is the starting point.

Magnitude of displacement = 0

Total path length = PQ + QR + RS + ST + TU + UP

= 500 + 500 + 500 + 500 + 500 + 500 = 3000 m

The motorist takes the eighth turn at point R.

The magnitude of displacement = PR

Therefore, the magnitude of displacement is 866.03 m at an angle of 30° with PR.

Total path length = Circumference of the hexagon + PQ + QR

= 6 × 500 + 500 + 500 = 4000 m

The magnitude of displacement and the total path length corresponding to the required turns is shown in the following table:

Q-11: A passenger arriving in a new town wants to go from the station to a hotel located 10 km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23 km long and reaches the hotel in 28 min.

(a) What is the average speed of the taxi?

(b) What is the magnitude of average velocity? Are the two equal?

(a) Total distance travelled = 23 km

Total time taken = 28 min = \(\begin{array}{l}\frac{28}{60}\end{array} \) h

= \(\begin{array}{l}\frac{23}{\frac{28}{60}}\end{array} \) = 49.29 km/h

(b) Distance between the hotel and the station = 10 km = Displacement of the car

Average velocity = \(\begin{array}{l}\frac{10}{\frac{28}{60}}\end{array} \) = 21.43 km/h

The two physical quantities are not equal.

Q-12: Rain is falling vertically with a speed of 30 \(\begin{array}{l}m s^{-1}\end{array} \) . A woman rides a bicycle with a speed of 10 \(\begin{array}{l}m s^{-1}\end{array} \) in the north-to-south direction. What is the direction in which she should hold her umbrella?

Ans: The described situation is shown in the given figure

In order to protect herself from the rain, the woman must hold her umbrella in the direction of the relative velocity (v) of the rain with respect to the woman.

= 30 + (-10) = 20 m/s

= \(\begin{array}{l}\tan ^{-1}\left ( 0.333 \right )\end{array} \) = 18°C

Hence, the woman must hold the umbrella toward the south, at an angle of nearly 18° with the vertical.

Q-13: A man can swim with a speed of 4 km/h in still water. How long does he take to cross a river 1 km wide if the river flows steadily at 3 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?

Speed of the man \(\begin{array}{l}v_{m}\end{array} \) = 4 km/h

Width of the river = 1 km

= \(\begin{array}{l}\frac{1}{4}\end{array} \) h

= \(\begin{array}{l}\frac{1}{4} \times 60\end{array} \) = 15 min

= \(\begin{array}{l}\frac{3}{4} \times 1000\end{array} \) = 750 m

Q-14: In a harbour, the wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?

Velocity of the boat = \(\begin{array}{l}v_{b}\end{array} \) = 51 km/h

Velocity of the wind = \(\begin{array}{l}v_{w}\end{array} \) = 72 km/h

The flag is fluttering in the northeast direction. It shows that the wind is blowing towards the northeast direction. When the ship begins sailing toward the north, the flag will move along the direction of the relative velocity ( \(\begin{array}{l}v_{wb}\end{array} \) ) of the wind with respect to the boat.

= \(\begin{array}{l}\tan ^{-1}\left ( 1.0038 \right )\end{array} \) = 45.11°

Angle with respect to the east direction = 45.11° – 45° = 0.11°

Hence, the flag will flutter almost due east.

Q-15: The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball is thrown with a speed of 40 \(\begin{array}{l}ms^{-1}\end{array} \) can go without hitting the ceiling of the hall?

Speed of the ball, u = 40 ms -1

Maximum height, h = 25 m

In projectile motion, the maximum height achieved by a body projected at an angle \(\begin{array}{l}\theta\end{array} \) is given as:

Horizontal range, R:

= \(\begin{array}{l}\frac{1600 \times 0.922}{9.8}\end{array} \) = 150.53 m

Q-16: A cricketer can throw a ball to a maximum horizontal distance of 100 m. How high above the ground can the cricketer throw the same ball?

The maximum horizontal distance, R = 100 m

The cricketer will only be able to throw the ball to the maximum horizontal distance when the angle of projection is 45°, i.e., \(\begin{array}{l}\theta\end{array} \) = 33.60°

The horizontal range for a projection velocity v is given as

R = \(\begin{array}{l}\frac{u^{2}\sin 2\theta}{g}\end{array} \) \(\begin{array}{l}100 = \frac{u^{2}}{g}\sin 90^{\circ}\end{array} \) \(\begin{array}{l}\frac{u^{2}}{g} = 100\end{array} \) —— (i)

The ball will achieve the max height when it is thrown vertically upward. For such motion, the final velocity v is 0 at the max height H.

Acceleration, a = – g

Using the 3 rd equation of motion

= \(\begin{array}{l}H = \frac{1}{2} \times 100\end{array} \) = 50 m

Q-17: A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the direction and magnitude of the acceleration of the stone?

Length of the string, l = 80 cm = 0.8 m

No. of revolutions = 14

Time taken = 25 s

Frequency, v = \(\begin{array}{l}\frac{No. \; of \; revolution}{Time \; taken}\end{array} \) = \(\begin{array}{l}\frac{14}{25}\end{array} \) Hz

Angular frequency \(\begin{array}{l}\omega\end{array} \) ,

Centripetal acceleration:

The direction of centripetal acceleration is always directed along the string, toward the centre, at all points.

Q-18: An aircraft executes a horizontal loop of radius 1 km with a steady speed of 900 km h -1 .Compare its centripetal acceleration with the acceleration due to gravity.

Radius of the loop, r = 1 km = 1000 m

Speed, v = 900 km h -1 = \(\begin{array}{l}900 \times \frac{5}{18}\end{array} \) = 250 ms -1

= \(\begin{array}{l}\frac{\left (250 \right )^{2}}{1000}\end{array} \) = 62.5 ms -2

Acceleration due to gravity, g = 9.8 ms -2

Q-19: Read each statement below carefully and state, with reasons, if it is true or false:

(a) The net acceleration of a particle in a circular motion is always along the radius of the circle towards the centre.

(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.

(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.

The net acceleration of a particle in a circular motion is always directed along the radius of the circle toward the centre only in the case of uniform circular motion.

At a point on a circular path, a particle appears to move tangentially to the circular path.

In uniform circular motion (UCM), the direction of the acceleration vector points toward the centre of the circle. However, it constantly changes with time. The average of these vectors over one cycle is a null vector.

Q-20: The position of a particle is given by

\(\begin{array}{l}r = 3.0t \;\hat{i} – 2.0t^{2} \;\hat{j} + 4.0 \hat{k} \; \;m\end{array} \)

Where t is in seconds, and the coefficients have the proper units for r to be in meters.

(a) Find the ‘v’ and ‘a’ of the particle?

(b) What is the magnitude and direction of the velocity of the particle at t = 2.0 s?

(a) The position of the particle is given by:

Velocity \(\begin{array}{l}\vec{v}\end{array} \) , of the particle is given as:

Acceleration \(\begin{array}{l}\vec{a}\end{array} \) , of the particle is given as:

8.54 m/s, \(\begin{array}{l}69.45^{\circ}\end{array} \) below the x-axis

At t = 2.0 s:

The magnitude of velocity is given by

The negative sign indicates that the direction of velocity is below the x-axis.

Q-21: A particle starts from the origin at t = 0 s with the velocity of \(\begin{array}{l}10 \; \hat{j} \; m \; s^{-1}\end{array} \) and moves in the x –y plane with a constant acceleration of \(\begin{array}{l}\left ( 8.0 \; \hat{i} + 2.0 \; \hat{j}\right ) \; m \; s^{-2}\end{array} \) .

(a) At what time is the x-coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?

(b) What is the speed of the particle at the time?

Integrating both sides:

Where, \(\begin{array}{l}\vec{u}\end{array} \) = velocity vector of the particle at t = 0

Integrating the equations with the conditions:

At t = 0; r = 0 and at t = t; r = r.

Since the motion of the particle is confined to the x-y plane, on equating the coefficients of \(\begin{array}{l}\hat{i} \; and \; \hat{j}\end{array} \) , we get

When x = 16 m:

Therefore, y = 10 × 2 + \(\begin{array}{l}\left (2 \right)^{2}\end{array} \) = 24 m

(b) Velocity of the particle:

At t = 2 s:

Therefore, the speed of the particle:

Q-22: \(\begin{array}{l}\vec{i}\end{array} \) and \(\begin{array}{l}\vec{j}\end{array} \) are unit vectors along x- and y-axis respectively. What is the magnitude and direction of the vectors \(\begin{array}{l}\vec{i}\end{array} \) + \(\begin{array}{l}\vec{j}\end{array} \) and \(\begin{array}{l}\vec{i}\end{array} \) − \(\begin{array}{l}\vec{j}\end{array} \)   ? What are the components of a vector \(\begin{array}{l}\vec{A}\end{array} \) = 2 \(\begin{array}{l}\vec{i}\end{array} \) and 3 \(\begin{array}{l}\vec{j}\end{array} \)   along the directions of \(\begin{array}{l}\vec{i}\end{array} \) + \(\begin{array}{l}\vec{j}\end{array} \)   and \(\begin{array}{l}\vec{i}\end{array} \)   – \(\begin{array}{l}\vec{j}\end{array} \) ? [You may use the graphical method]

Consider a vector \(\begin{array}{l}\vec{P}\end{array} \) , given as below,

Comparing the components on both sides, we get

Therefore, the magnitude of the vector \(\begin{array}{l}\vec{i} + \vec{j}\end{array} \) is \(\begin{array}{l}\sqrt{2}\end{array} \) .

Let \(\begin{array}{l}\theta\end{array} \) be the angle made by the vector \(\begin{array}{l}\vec{P}\end{array} \) , with the x-axis as given in the figure below.

Therefore, the vector \(\begin{array}{l}\vec{i} – \vec{j}\end{array} \) makes an angle of \(\begin{array}{l}45^{\circ}\end{array} \) with the x axis.

Let \(\begin{array}{l}\vec{Q} = \hat{i} – \hat{j}\end{array} \) \(\begin{array}{l}Q_{x}\; \hat{i} – Q_{y}\; \hat{j}= \hat{i} – \hat{j}\end{array} \) \(\begin{array}{l}Q_{x}\; = Q_{y}\; = 1\end{array} \) \(\begin{array}{l}\left | \vec{Q} \right | = \sqrt{Q_{x}^{2} + Q_{y}^{2}}\end{array} \) \(\begin{array}{l}\left | \vec{Q} \right | = \sqrt{2}\end{array} \) —— (iii)

Therefore, the magnitude of the vector \(\begin{array}{l}\hat{1} – \hat{j}\end{array} \) is \(\begin{array}{l}\sqrt{2}\end{array} \) .

Let \(\begin{array}{l}\theta\end{array} \) be the angle by the vector \(\begin{array}{l}\vec{Q}\end{array} \) , with the x–axis as given in the figure below,

Therefore, the vector \(\begin{array}{l}\vec{i} – \vec{j}\end{array} \) makes an angle of \(\begin{array}{l}-45^{\circ}\end{array} \) with the x-axis.

It is given that,

Let \(\begin{array}{l}\vec{A_{x}}\end{array} \) make an angle \(\begin{array}{l}\theta\end{array} \) with the x-axis, as it is shown in the figure,

Angle between the vectors \(\begin{array}{l}\left ( 2 \hat{i} + 3 \hat{j}\right )\end{array} \) and \(\begin{array}{l}\left ( \hat{i} + \hat{j}\right )\end{array} \) ,

Components of vector \(\begin{array}{l}\vec{A}\end{array} \) , along the direction of \(\begin{array}{l}\vec{P}\end{array} \) , making an angle \(\begin{array}{l}\theta\end{array} \) .

= \(\begin{array}{l}\frac{5}{\sqrt{2}}\end{array} \) —– (v)

Component of vector \(\begin{array}{l}\vec{A}\end{array} \) , along the direction of \(\begin{array}{l}\vec{Q}\end{array} \) , making an angle \(\begin{array}{l}\theta\end{array} \) .

= \(\begin{array}{l}-\frac{1}{\sqrt{2}}\end{array} \) —– (iv)

Q-23: Which of the given relations is true for any arbitrary motion in space?

(a) \(\begin{array}{l}v_{average} = \left (\frac{1}{2} \right )\left ( v\left ( t_{1} \right ) + v\left ( t_{2} \right ) \right )\end{array} \)

(b) \(\begin{array}{l}v_{average} = \frac{\left [ r\left ( t_{2} \right ) – r\left ( t_{1} \right )\right ]}{\left ( t_{2} – t_{1}\right )}\end{array} \)

(c) \(\begin{array}{l}v(t) = v\left ( 0 \right ) + at\end{array} \)

(d) \(\begin{array}{l}r(t) = r(0) + v(0)t + \left (\frac{1}{2} \right )at^{2}\end{array} \)

(e) \(\begin{array}{l}a_{average} = \frac{\left [ v\left ( t_{2} \right ) – v\left ( t_{1} \right )\right ]}{\left ( t_{2} – t_{1}\right )}\end{array} \)

It is given that the motion of the particle is arbitrary. Therefore, the average velocity of the particle cannot be given by this equation.

The arbitrary motion of the particle can be represented by this equation.

The motion of the particle is arbitrary. The acceleration of the particle may also be non-uniform. Hence, this equation cannot represent the motion of the particle in space.

The motion of the particle is arbitrary; the acceleration of the particle may also be non-uniform. Hence, this equation cannot represent the motion of a particle in space.

Q-24: Read each statement below carefully and state, with reasons and examples, if it is true or false.

A scalar quantity is one that

(a) is conserved in a process

(b) can never take negative values

(c) must be dimensionless

(d) does not vary from one point to another in space

(e) has the same value for observers with different orientations of axes  

Despite being a scalar quantity, energy is not conserved in inelastic collisions.

Despite being a scalar quantity, the temperature can take negative values.

The total path length is a scalar quantity. Yet it has the dimension of length.

A scalar quantity such as gravitational potential can vary from one point to another in space.

The value of a scalar does not vary for observers with different orientations of axes.

Q.25. An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is 30°, what is the speed of the aircraft?

Height at which the aircraft is flying = 3400 m

Let A and B be the positions of the aircraft, making an angle ∠AOB = 30 0 . The perpendicular OC is drawn on AB. Here, OC is the height of the aircraft, which is equal to 3400 m and ∠AOC =  ∠COB = 15 0 .

In the ΔAOC, AC = OC tan 15 0 = 3400 x 0.267 = 910.86 m

AB = AC + CB = AC + AC = 2 AC = 2 x 910.86 m

Speed of the aircraft = distance AB/time = (2 x 910.86)/10= 182.17 m/s =182.2 m/s

Q-26: Does a vector have a location in space? Will it fluctuate with time?  Can two equivalent vectors, x and y, at various locations in space fundamentally have indistinguishable physical effects? Give cases in support of your answer.

No, Yes and No.

A vector in space has no distinct location. The reason behind this is that a vector stays invariant when it displaces in a way that its direction and magnitude do not change. Although, a position vector has a distinct location in space.

A vector changes with time. For instance, the velocity vector of a ball moving with a specific speed fluctuates with time.

Two equivalent vectors situated at different locations in space do not generate the same physical effect. For instance, two equivalent forces acting at different points on a body tend to rotate the body, but the combination will not generate the equivalent turning effect.

Q-27: As a vector is having both direction and magnitude, then is it necessary that if anything is having direction and magnitude, it is termed as a vector? The rotation of an object is defined by the angle of rotation about the axis and the direction of rotation of the axis. Will it be a rotation of a vector?

A physical quantity which is having both direction and magnitude is not necessarily a vector. For instance, in spite of having direction and magnitude, the current is a scalar quantity. The basic necessity for a physical quantity to fall in a vector category is that it ought to follow the “law of vector addition”.

As the rotation of a body about an axis does not follow the basic necessity to be a vector, i.e., it does not follow the “law of vector addition”, so it is not a vector quantity. Although in some cases, rotation of a body about an axis by a small angle follows the law of vector addition, so it is termed a vector.

Q-28: Can we associate a vector with

(i) a sphere

(ii) the length of a wire bent into a loop

(iii) a plane area

Clarify for the same.

No, No, Yes

(i) We can’t associate the volume of a sphere with a vector, but the area of a sphere can be associated with an area vector.

(ii) We can’t associate the length of a wire bent into a loop with a vector.

(iii) We can associate a plane area with a vector.

Q. 29. A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.

A bullet is fired at an angle = 30°

The bullet hits the ground at a distance of 3km = 3000 m

Horizontal range, R = u 2 sin2θ/g

3000 = u 2 sin 60 0 /9.8

u 2 = (3000 x 9.8)/(√3/2)

= 2 (3000 x 9.8)/√3 = 58800/1.732 = 33949

Also, R’ = u 2 sin 2θ/g ⇒ 5000 = (33949 x sin2θ)/9.8

Sin 2θ = (5000 x 9.8)/33949 = 49000/33949  =1.44

The sine of an angle cannot be more than 1. Therefore, a target 5 km away cannot be hit

Q. 30. A fighter plane flying horizontally at an altitude of 1.5 km with a speed of 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s -1 to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take g = 10 m s -2 ).

Speed of the fighter plane = 720 km/h = 720 x (5/18) = 200 m/s

The altitude of the plane = 1.5 km

Velocity of the shell = 600 m/s

Sin θ = 200/600 = 1/3

θ = sin -1 (1/3) = 19.47 0

Let H be the minimum altitude.

Using equation,

H = u 2 sin 2 (90 – θ)/2g

= (600 2  cos 2 θ)/2g

= 600 2 cos 2 θ/(2 x 9.8)= {360000[(1+cos 2θ)/2]}/2g

= 360000[1+cos2 (19.470)/2]/2g

= 360000[ (1 + cos 38.94)/2]/(2 x 9.8)

= 360000 [ (1 + 0.778)/2]/19.6

= 360000 [(1.778/2)]/19.6

= (360000 x 0.889) /19.6

= 320040/19.6

= 16328 m = 16.328 km

Q. 31.  A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of a radius of 80 m, he applies brakes and reduces his speed at the constant rate of  0.50 m/s every second. What is the magnitude and direction of the net acceleration of  the cyclist on the circular turn?

Speed of the cyclist = 27 km/h = 27 x (5/18) = 7.5 m/s

The radius of the road = 80 m

The net acceleration is due to the braking and the centripetal acceleration.

Due to braking, a =  0.50 m/s 2

Centripetal acceleration, a = v 2 /2 = (7.5) 2 /80 = 0.70 m/s 2

Since the angle between a c and a T is 90 o , the resultant acceleration is given by

= 0.86 m/s 2

and tan β = a c /a t = 0.7/0.5 = 1.4

β = tan -1 (1.4) = 54.5 0 from the direction of velocity

Q.32.  (a) Show that for a projectile, the angle between the velocity and the x-axis as a function of time is given by

\(\begin{array}{l}\theta (t)=tan^{-1}(\frac{v_{0y-gt}}{v_{ox}})\end{array} \)

(b) Shows that the projection angle θ 0 for a projectile launched from the origin is  given by

\(\begin{array}{l}\theta_{0}=tan^{-1}(\frac{4h_{m}}{R})\end{array} \)

where the symbols have their usual meaning

(a) Let θ be the angle at which the projectile is fired w.r.t the x-axis

θ depends on t

Therefore, tan θ(t) = v x /v y = (v oy – gt)/v 0x   (since v y = v 0y -gt and v x =v ox )

θ(t) = tan -1 ((v oy – gt)/v 0x )

(b) Since, h max = u 2 sin 2 θ/2g —–(1)

R = u 2 sin2θ/g——–(2)

Dividing (1) by (2)

(h max /R) =  [u 2 sin 2 θ/2g]/[ u 2 sin2θ/g] = tan θ/4

θ = tan -1 (4 h max /R)

Along with answers to the textbook question, this solution has extra questions, NCERT Exemplar problems , worksheets, MCQs, Short and Long-answer questions. These solutions help you in preparing for the Class 11 examinations and entrance examinations students will face after the Class 12 exams.

Here, we will come across questions related to the scalar and vector quantities in physics, and we are pretty much aware of the difference between scalar and vector. We will be performing algebraic expressions on various scalar quantities. We will be coming up with true and false questions, and students have to provide a statement behind their reasons with respect to these physical quantities. We will be drawing vector inequalities of various quantities. You can check out NCERT Solutions for Class 11 Physics for more chapter-wise solutions.

In addition, we will be seeing questions on the magnitude of vectors and their co-linearity and will be finding the magnitude of the displacement vector of three girls skating in a circular ground. We will be finding the position of a man after he cycles along a circular path. We will be comparing the various type of displacement of a motorist. We will be seeing an adventurous journey of a passenger who newly arrived in a town and how he got tricked by a cab driver.

How does it feel when you are riding your bicycle in the rain, and the raindrops fall on your face at a certain angle? We will be seeing how much time a man takes to swim across a river and how much distance he has to swim if the water is not still. Have you ever thrown a ball to your ceiling? You can throw the ball across long distances now. We will see how a cricketer throws a ball so long to the wicketkeeper.

What about the vector quantities in space? Do they still have a location and position? Find it out below. We will learn here how to arrange our height while throwing a ball so that we can achieve a particular distance target. How to shoot a helicopter in order to hit the helicopter, and at what height can a pilot fly a helicopter from the ground? All these questions can be answered after looking at the solutions provided here. Do you know why a biker reduces his speed at the turn and what he will do otherwise? Find out why.

BYJU’S is committed to providing the best study material, notes, Class 11 Physics sample papers, previous year question papers, worksheets, MCQs, videos and animations for the benefit of Class 11 Science students. To get access to all the resources provided by BYJU’S, download the BYJU’S learning App.

Important Concepts of NCERT Solutions for Class 11 Physics Chapter 4

Motion in a Plane is one of the important chapters in Unit-II Kinematics of Class 11 Physics, which carries higher marks in the exam. To score remarkable grades, students are recommended to refer to the NCERT Solutions from BYJU’S which are present in both online and offline modes. Some of the important concepts covered in the NCERT Solutions for Class 11 Physics Chapter 4 are

4.1 INTRODUCTION

4.2 SCALARS AND VECTORS

4.2.1 Position and Displacement Vectors

4.2.2 Equality of Vectors

4.3 MULTIPLICATION OF VECTORS BY REAL NUMBERS

4.4 ADDITION AND SUBTRACTION OF VECTORS — GRAPHICAL METHOD

4.5 RESOLUTION OF VECTORS

4.6 VECTOR ADDITION – ANALYTICAL METHOD

4.7 MOTION IN A PLANE

4.7.1 Position Vector and Displacement

4.8 MOTION IN A PLANE WITH CONSTANT ACCELERATION

4.9 RELATIVE VELOCITY IN TWO DIMENSIONS

4.10 PROJECTILE MOTION

4.11 UNIFORM CIRCULAR MOTION

Disclaimer – 

Dropped Topics – 

4.9 Relative Velocity in Two Dimensions Exercises 4.12–4.14; 4.26–4.32

Frequently Asked Questions on NCERT Solutions for Class 11 Physics Chapter 4

What type of questions is present in chapter 4 motion in a plane of ncert solutions for class 11 physics, what will we learn in chapter 4 of ncert solutions for class 11 physics, where can i get the ncert solutions for class 11 physics chapter 4 online, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.