planck's quantum hypothesis formula

• Structure of Atom
• Planks Quantum Theory

Planck's Quantum Theory - Quantization Of Energy

Introduction.

Before learning about Planck’s quantum theory, we need to know a few things.

As progress in the science field was happening, Maxwell’s suggestion about the wave nature of electromagnetic radiation was helpful in explaining phenomena such as interference, diffraction, etc. However, he failed to explain various other observations such as the nature of emission of radiation from hot bodies, photoelectric effect, i.e. ejection of electrons from a metal compound when electromagnetic radiation strikes it, the dependence of heat capacity of solids upon temperature, line spectra of atoms (especially hydrogen).

Table of Contents

Black body radiation, recommended videos.

• Planck’s quantum theory
• Frequently Asked Questions – FAQs

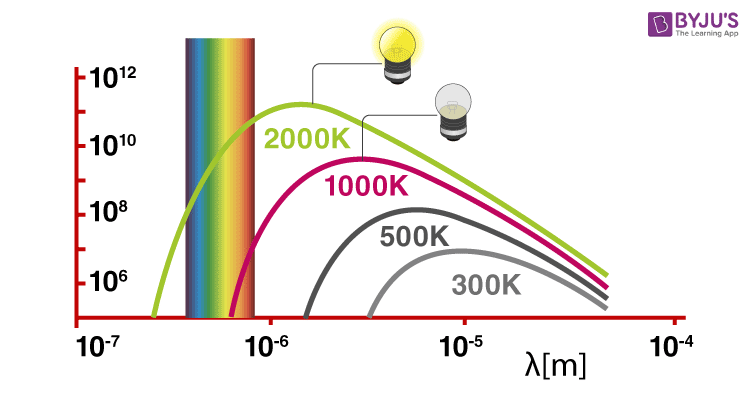
Solids, when heated, emit radiation varying over a wide range of wavelengths. For example: when we heat solid colour, changes continue with a further increase in temperature. This change in colour happens from a lower frequency region to a higher frequency region as the temperature increases. For example, in many cases, it changes from red to blue. An ideal body which can emit and absorb radiation of all frequencies is called a black body. The radiation emitted by such bodies is called black body radiation.

Thus, we can say that variation of frequency for black body radiation depends on the temperature. At a given temperature, the intensity of radiation is found to increase with an increase in the wavelength of radiation which increases to a maximum value and then decreases with an increase in the wavelength. This phenomenon couldn’t be explained with the help of Maxwell’s suggestions. Hence, Planck proposed Planck’s quantum theory to explain this phenomenon.

Black body Radiation

Planck’s Quantum Theory

According to Planck’s quantum theory,

• Different atoms and molecules can emit or absorb energy in discrete quantities only. The smallest amount of energy that can be emitted or absorbed in the form of electromagnetic radiation is known as quantum.
• The energy of the radiation absorbed or emitted is directly proportional to the frequency of the radiation.

Meanwhile, the energy of radiation is expressed in terms of frequency as,

E = Energy of the radiation

h = Planck’s constant (6.626×10 –34  J.s)

ν = Frequency of radiation

Interestingly, Planck has also concluded that these were only an aspect of the processes of absorption and emission of radiation. They had nothing to do with the physical reality of the radiation itself. Later in the year 1905, famous German physicist, Albert Einstein also reinterpreted Planck’s theory to further explain the photoelectric effect. He was of the opinion that if some source of light was focused on certain materials, they can eject electrons from the material. Basically, Planck’s work led Einstein in determining that light exists in discrete quanta of energy, or photons.

Related Videos

Electromagnetic radiations & planck’s quantum theory.

Frequently Asked Questions on Black Body Radiation

What is a planck curve.

A black body’s energy density between λ and λ + dλ is the energy of a mode E = hc / λ times the density of photon states, times the probability that the mode is filled. This is the famous formula from Planck for a black body’s energy density.

What is Stefan’s law of radiation?

The law of Stefan-Boltzmann states that the overall radiant heat power released from a surface is proportional to its fourth absolute temperature power. The rule only refers to black bodies, imaginary surfaces that collect heat radiation from all events.

How is blackbody radiation produced?

Electromagnetic radiation is produced from all objects according to their temperature. An idealised object that consumes the electromagnetic energy that it comes into contact with is a black body. In a continuous continuum, which then emits thermal radiation according to its temperature.

What is Planck’s constant in simple terms?

The Planck constant compares the sum of energy a photon bears with its electromagnetic wave frequency. It is named after Max Planck, the physicist. In quantum mechanics, it is an essential quantity.

What is Planck’s number?

Planck’s constant is currently calculated by scientists to be 6.62607015 x 10 -34 joule-seconds. In 1900, Planck identified his game-changing constant by describing how the smallest bits of matter release energy in discrete bundles called quanta, essentially placing the “quanta” in quantum mechanics.

To learn more about the  quantum theory of light and other topics you can register with BYJU’S or download BYJU’s – The Learning App.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Chemistry related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

i liked your material you have given

Thank you so much.

I like it. It helps with my chemistry homework.

Good job keep it.

It’s good

softly captured, keep it up

thnx a lott

love you BYJU’S FOREVER

thank you so much, helped with my essay on Max Planck

Thank you byjus awesome it helped me a lot in my project

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Humanities ›
• History & Culture ›
• The 20th Century ›
• People & Events ›

Max Planck Formulates Quantum Theory

Bettmann / Getty Images

• People & Events
• Fads & Fashions
• Early 20th Century
• American History
• African American History
• African History
• Ancient History and Culture
• Asian History
• European History
• Latin American History
• Medieval & Renaissance History
• Military History
• Women's History
• B.A., History, University of California at Davis

In 1900, German theoretical physicist Max Planck revolutionized the field of physics by discovering that energy does not flow evenly but is instead released in discrete packets. Planck created an equation to predict this phenomenon, and his discovery ended the primacy of what many people now call "classical physics" in favor of the study of quantum physics .

The Problem

Despite feeling that all was already known in the field of physics, there was still one problem that had plagued physicists for decades: They could not understand the surprising results they continued to get from heating surfaces that absorb all frequencies of light that hit them, otherwise known as black bodies .

Try as they might, scientists could not explain the results using classical physics.

The Solution

Max Planck was born in Kiel, Germany, on April 23, 1858, and was considering becoming a professional pianist before a teacher turned his attention to science. Planck went on to receive degrees from the University of Berlin and the University of Munich.

After spending four years as an associate professor of theoretical physics at Kiel University, Planck moved to the University of Berlin, where he became a full professor in 1892.

Planck's passion was thermodynamics. While researching black-body radiation, he too kept running into the same problem as other scientists. Classical physics could not explain the results he was finding.

In 1900, 42-year-old Planck discovered an equation that explained the results of these tests: E=Nhf, with E=energy, N=integer, h=constant, f=frequency. In determining this equation, Planck came up with the constant (h), which is now known as " Planck's constant ."

The amazing part of Planck's discovery was that energy, which appears to be emitted in wavelengths, is actually discharged in small packets he called "quanta".

This new theory of energy revolutionized physics and opened the way for Albert Einstein's theory of relativity .

Life After Discovery

At first, the magnitude of Planck's discovery was not fully understood. It wasn't until Einstein and others used quantum theory for even further advancements in physics that the revolutionary nature of his discovery was realized.

By 1918, the scientific community was well aware of the importance of Planck's work and awarded him the Nobel Prize in Physics.

He continued to conduct research and contribute further to the advancement of physics, but nothing compared to his 1900 findings.

Tragedy in His Personal Life

While he achieved much in his professional life, Planck's personal life was marked by tragedy. His first wife died in 1909, his oldest son, Karl, during  World War I . Twin girls, Margarete and Emma, both later died in childbirth. And his youngest son, Erwin, was implicated in the failed  July Plot to kill Hitler and was hanged.

In 1911, Planck did remarry and had one son, Hermann.

Planck decided to remain in Germany during World War II . Using his clout, the physicist tried to stand up for Jewish scientists, but with little success. In protest, Planck resigned as president of the Kaiser Wilhelm Institute in 1937.

In 1944, a bomb dropped during an Allied air raid hit his house, destroying many of his possessions, including all his scientific notebooks. 

Max Planck died on October 4, 1947, at the age of 89.

• Most Influential Scientists of the 20th Century
• 10 Things You Don't Know About Albert Einstein
• Biography of Albert Einstein, Theoretical Physicist
• Biography of Enrico Fermi
• Cold War Glossary
• Sigmund Freud
• Clarence Darrow, Famous Defense Attorney and Crusader for Justice
• Sinking of the Lusitania
• What Is Communism? Definition and Examples
• A Timeline of the Genocide in Rwanda
• 100 Famous Women of the 20th Century
• Life and Work of H.L. Mencken: Writer, Editor, and Critic
• History of the Sacco and Vanzetti Case
• A Short Guide to the Vietnam War
• The Day the Mona Lisa Was Stolen
• Biography of Helen Keller, Deaf and Blind Spokesperson and Activist

Wigner entropy conjecture and the interference formula in quantum phase space

Wigner-positive quantum states have the peculiarity to admit a Wigner function that is a genuine probability distribution over phase space. The Shannon differential entropy of the Wigner function of such states – called Wigner entropy for brevity – emerges as a fundamental information-theoretic measure in phase space and is subject to a conjectured lower bound, reflecting the uncertainty principle. In this work, we prove that this Wigner entropy conjecture holds true for a broad class of Wigner-positive states known as beam-splitter states, which are obtained by evolving a separable state through a balanced beam splitter and then discarding one mode. Our proof relies on known bounds on the p 𝑝 p italic_p -norms of cross-Wigner functions and on the interference formula, which relates the convolution of Wigner functions to the squared modulus of a cross-Wigner function. Originally discussed in the context of signal analysis, the interference formula is not commonly used in quantum optics although it unveils a strong symmetry exhibited by Wigner functions of pure states. We provide here a simple proof of the formula and highlight some of its implications. Finally, we prove an extended conjecture on the Wigner-Rényi entropy of beam-splitter states, albeit in a restricted range for the Rényi parameter α ≥ 1 / 2 𝛼 1 2 \alpha\geq 1/2 italic_α ≥ 1 / 2 .

I Introduction

Quantum phase space. The phase-space representation of quantum mechanics has emerged as a powerful and insightful framework for understanding and analyzing quantum systems. By providing a bridge between the quantum and classical worlds, this approach improves our understanding of quantum systems and opens new research avenues in quantum science. This representation not only provides a more intuitive description of quantum phenomena but also facilitates the study of the quantum-classical correspondence, which is crucial for the development of quantum technologies in particular when dealing with continuous-variable systems. In short, quantum phase space has proven to be a privileged locus to identify quantum properties and resources [ 1 , 2 , 3 , 4 , 5 ] .

Wigner negativity. Although there exist multiple representations of a quantum state in phase space, the Wigner function appears as the prominent tool for that purpose [ 6 ] . It indeed benefits from a collection of useful features that make it stand out from its alternatives (see Sec. II ). It serves as the closest quantum analogue to the classical phase-space distribution, offering a complete description of the quantum state while retaining many properties of classical probabilities. However, unlike classical probability distributions, the Wigner function can take on negative values, reflecting the intrinsic non-classicality and coherence of quantum states. This feature is particularly significant in exploring fundamental quantum effects such as quantum entanglement, interference, and the behavior of quantum systems under measurement. More generally, the negativity of the Wigner function has been widely recognized as a quantum resource [ 7 , 8 , 1 ] . Hence, the Wigner representation effects a fundamental divide between two classes of quantum states: there are Wigner-negative states, which fail to be described by a probability distribution, and Wigner-positive states, which admit a fully classical probabilistic description. The focus of this work will be on the latter. Although they may wrongly appear as irrelevant in a study of quantum states since they are devoid of negativity, Wigner-positive states remain subject to the laws of quantum physics and can exhibit intrinsically quantum features (think of the squeezing of light, for example).

\mathcal{W}_{+} caligraphic_W start_POSTSUBSCRIPT + end_POSTSUBSCRIPT can be pictured as a buffer at the crossroads of quantum states and classical probability distributions.

The quantum-classical border. Because of this buffer zone, the border between the sets 𝒬 𝒬 \mathcal{Q} caligraphic_Q and 𝒫 𝒫 \mathcal{P} caligraphic_P is two-fold: there is a classical boundary as well as a quantum boundary, as schematically depicted in Fig.  1 . The classical boundary (near the hatched blue region) delimits Wigner-positive and Wigner-negative states; the quantum boundary (near the solid blue region) delimits quantum and non-quantum probability distributions depending on whether the associated trace-1 operator is PSD or not. From a classical point of view, the quantum boundary has nothing special: in fact, it teaches us about the limits of the quantum world. It is linked to the question of when a probability distribution cease to be a valid Wigner function. Mathematically, this question has a clear answer: a Wigner function becomes invalid as soon as its corresponding trace-1 operator fails to be positive semi-definite [ 9 , 10 , 11 , 12 ] . Yet, this answer can be viewed as unsatisfactory because it lacks a tangible interpretation in phase space. Along this direction, a collection of requirements for physicality have been known: a valid Wigner function should be continuous and bounded, its covariance matrix is constrained by the uncertainty principe [ 13 ] , and entropic bounds apply to its marginal distributions [ 14 , 15 ] . Such necessary conditions are insightful inasmuch as they inform us about the shape of admissible Wigner functions. Complementing them with any other criteria helps us draw the line with more precision between quantum and non-quantum probability distributions.

The Wigner entropy. Within the set of Wigner-positive operators 𝒫 𝒫 \mathcal{P} caligraphic_P , the toolbox of information theory is readily applicable and it makes perfect sense to define the Shannon differential entropy of a phase-space probability distribution, which is nothing else but the Gibbs entropy of statistical mechanics. Here, we call it the Wigner entropy [ 16 ] , which captures phase-space uncertainty with an information-theoretic flavor. From the classical point of view, the Wigner entropy could seemingly be arbitrarily low for highly “peaked” states. However, the situation is different in quantum as it is subject to the uncertainty principle. Because of that, it is sensible to anticipate that, for quantum Wigner-positive states, the Wigner entropy cannot fall below some critical threshold. This observation is encapsulated by the Wigner entropy conjecture [ 16 ] , which states a precise lower bound to the Wigner entropy (see Sec. II ). The conjecture has attracted an increasing attention recently [ 17 , 16 , 18 , 19 , 20 , 21 ] but remains open as of today. As we elaborate in Sec. II , the Wigner entropy also benefits from other noteworthy properties, which support its status as physical quantity of its own right. Provided it is true, the Wigner entropy conjecture unravels a new facet of the quantum-classical border.

Contribution of this work. In this work, we present new evidences towards the validity of the Wigner entropy conjecture. We prove that it holds true for a large family of Wigner-positive states, known as beam-splitter states  [ 16 ] (see Sec.  III ). Our result mainly relies on two different ingredients: the interference formula [ 22 , 23 ] , which links the square of a Wigner function to its convolution with itself, and bounds on the p 𝑝 p italic_p -norms of cross Wigner functions [ 24 ] . Further, we are able to prove an extended version of the Wigner entropy conjecture formulated in terms of Rényi entropy of the Wigner function (see Sec. II ) for beam-splitter states, albeit in some restricted range of the Rényi parameter.

The interference formula. This formula, which appears to be well established in the context of radar ambiguity functions and time-frequency signal analysis [ 22 , 23 ] , seems to be much less known in a quantum optical context. Yet, as we shall see, it appears to be a very powerful tool and a fundamental relation obeyed by the Wigner function of any pure state. It highly constrains the shape of Wigner functions and unveils a “self-convolution” symmetry obeyed by all pure states. In this sense, it is a key ingredient in defining what makes a Wigner function valid. As it is a central ingredient for our result, and since we believe it deserves more visibility in the quantum optics community, we devote Sec. IV to highlight this formula.

The present paper is organized as follows. In Sec. II we introduce our notation for the phase-space formalism. We define the Wigner entropy and present the Wigner entropy conjecture. We also define the Wigner-Rényi entropy and formulate an extended conjecture. Sec. III is devoted to beam-splitter states. In Sec. IV we introduce the interference formula. In Sec. V , we present our main results. Finally, we discuss our results and conclude in Sec. VI .

II Preliminaries

Here, we lay out our notations and the technical tools that will be used in the following Sections. We begin with a short overview of the phase-space formalism in terms of Wigner functions. We then introduce the Wigner entropy and recall the associated Wigner conjecture. Finally, we present a generalization of this conjecture involving the Wigner-Rényi entropy.

^ 𝑥 𝑖 ^ 𝑝 2 \hat{a}=(\hat{x}+i\hat{p})/\sqrt{2} over^ start_ARG italic_a end_ARG = ( over^ start_ARG italic_x end_ARG + italic_i over^ start_ARG italic_p end_ARG ) / square-root start_ARG 2 end_ARG and photon-number operator n ^ = a ^ † ⁢ a ^ ^ 𝑛 superscript ^ 𝑎 † ^ 𝑎 \hat{n}=\hat{a}^{\dagger}\hat{a} over^ start_ARG italic_n end_ARG = over^ start_ARG italic_a end_ARG start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT over^ start_ARG italic_a end_ARG . We define the displacement operator D ^ ⁢ ( α ) = exp ⁢ ( α ⁢ a ^ † − α ∗ ⁢ a ^ ) ^ 𝐷 𝛼 exp 𝛼 superscript ^ 𝑎 † superscript 𝛼 ∗ ^ 𝑎 \hat{D}(\alpha)=\mathrm{exp}(\alpha\hat{a}^{\dagger}-\alpha^{\ast}\hat{a}) over^ start_ARG italic_D end_ARG ( italic_α ) = roman_exp ( italic_α over^ start_ARG italic_a end_ARG start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT - italic_α start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT over^ start_ARG italic_a end_ARG ) with α ∈ ℂ 𝛼 ℂ \alpha\in\mathbb{C} italic_α ∈ blackboard_C and the parity operator Π ^ = ( − 1 ) n ^ ^ Π superscript 1 ^ 𝑛 \hat{\Pi}=(-1)^{\hat{n}} over^ start_ARG roman_Π end_ARG = ( - 1 ) start_POSTSUPERSCRIPT over^ start_ARG italic_n end_ARG end_POSTSUPERSCRIPT . Finally, we denote the displaced parity operator as Π ^ ⁢ ( α ) = D ^ ⁢ ( α ) ⁢ Π ^ ⁢ D ^ † ⁢ ( α ) ^ Π 𝛼 ^ 𝐷 𝛼 ^ Π superscript ^ 𝐷 † 𝛼 \hat{\Pi}(\alpha)=\hat{D}(\alpha)\hat{\Pi}\hat{D}^{\dagger}(\alpha) over^ start_ARG roman_Π end_ARG ( italic_α ) = over^ start_ARG italic_D end_ARG ( italic_α ) over^ start_ARG roman_Π end_ARG over^ start_ARG italic_D end_ARG start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT ( italic_α ) .

𝑝 2 Im 𝛼 p\mapsto p+\sqrt{2}\,\mathrm{Im(\alpha)} italic_p ↦ italic_p + square-root start_ARG 2 end_ARG roman_Im ( italic_α ) . The reason for this choice is that the definition ( 4 ) of the Wigner entropy then coincides with its earlier definition in terms of ( x , p ) 𝑥 𝑝 (x,p) ( italic_x , italic_p ) coordinates, see [ 16 ] . :

The above relation is known as the overlap formula or Moyal’s identity [ 27 ] .

𝑥 𝑖 𝑝 \alpha=x+ip italic_α = italic_x + italic_i italic_p , the position distribution is given by ρ x ⁢ ( x ) := ⟨ x | ⁢ ρ ^ ⁢ | x ⟩ = ∫ W ρ ⁢ ( x , p ) ⁢ d p assign subscript 𝜌 𝑥 𝑥 bra 𝑥 ^ 𝜌 ket 𝑥 subscript 𝑊 𝜌 𝑥 𝑝 𝑝 \rho_{x}(x)\vcentcolon=\bra{x}\hat{\rho}\ket{x}=\int W_{\rho}(x,p)\differential p italic_ρ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ( italic_x ) := ⟨ start_ARG italic_x end_ARG | over^ start_ARG italic_ρ end_ARG | start_ARG italic_x end_ARG ⟩ = ∫ italic_W start_POSTSUBSCRIPT italic_ρ end_POSTSUBSCRIPT ( italic_x , italic_p ) start_DIFFOP roman_d end_DIFFOP italic_p while the momentum distribution is given by ρ p ⁢ ( p ) := ⟨ p | ⁢ ρ ^ ⁢ | p ⟩ = ∫ W ρ ⁢ ( x , p ) ⁢ d x assign subscript 𝜌 𝑝 𝑝 bra 𝑝 ^ 𝜌 ket 𝑝 subscript 𝑊 𝜌 𝑥 𝑝 𝑥 \rho_{p}(p)\vcentcolon=\bra{p}\hat{\rho}\ket{p}=\int W_{\rho}(x,p)\differential x italic_ρ start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ( italic_p ) := ⟨ start_ARG italic_p end_ARG | over^ start_ARG italic_ρ end_ARG | start_ARG italic_p end_ARG ⟩ = ∫ italic_W start_POSTSUBSCRIPT italic_ρ end_POSTSUBSCRIPT ( italic_x , italic_p ) start_DIFFOP roman_d end_DIFFOP italic_x . Since density operators are positive semi-definite, ρ x subscript 𝜌 𝑥 \rho_{x} italic_ρ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and ρ p subscript 𝜌 𝑝 \rho_{p} italic_ρ start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT are genuine (non-negative) probability distributions.

\mathcal{W}_{+} caligraphic_W start_POSTSUBSCRIPT + end_POSTSUBSCRIPT . A state that is not Wigner positive is called Wigner negative. The picture becomes more intricate when considering mixed states, and, as of today, there is no satisfying description of the set of mixed Wigner-positive states [ 29 , 30 , 31 ] . Some common subsets of the set of Wigner-positive states are the convex hull of Gaussian states, passive states [ 32 , 33 ] , and beam-splitter states [ 16 ] . We will give an overview of beam-splitter states in Sec. III .

Wigner entropy. Since Wigner-positive states are described by a genuine probability distribution W ρ subscript 𝑊 𝜌 W_{\rho} italic_W start_POSTSUBSCRIPT italic_ρ end_POSTSUBSCRIPT over phase space, the Shannon differential entropy of W ρ subscript 𝑊 𝜌 W_{\rho} italic_W start_POSTSUBSCRIPT italic_ρ end_POSTSUBSCRIPT is mathematically well defined.

Definition 1 (Wigner entropy  [ 16 ] ) .

\hat{\rho}\in\mathcal{W}_{+} over^ start_ARG italic_ρ end_ARG ∈ caligraphic_W start_POSTSUBSCRIPT + end_POSTSUBSCRIPT is defined as

ℎ subscript 𝜌 𝑥 ℎ subscript 𝜌 𝑝 h(W)\leq h(\rho_{x})+h(\rho_{p}) italic_h ( italic_W ) ≤ italic_h ( italic_ρ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ) + italic_h ( italic_ρ start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ) [ 16 ] . Arguably, the Wigner entropy is the most natural information-theoretic measure of phase-space uncertainty, though it only has a clear meaning for Wigner-positive states. To date, the Wigner entropy has no established generalization to Wigner-negative states (note that a complex-valued extension of the Wigner entropy has recently been considered [ 19 ] ). Since the uncertainty principle forbids a simultaneous determination of position and momentum, it is natural to expect a critical minimum value for the Wigner entropy, which is the rationale for the following conjecture.

Conjecture 1 (Wigner entropy conjecture [ 16 ] ) .

The Wigner entropy of a Wigner-positive state satisfies the following lower bound:

ℎ subscript 𝜌 𝑥 ℎ subscript 𝜌 𝑝 h(W_{\rho})\leq h(\rho_{x})+h(\rho_{p}) italic_h ( italic_W start_POSTSUBSCRIPT italic_ρ end_POSTSUBSCRIPT ) ≤ italic_h ( italic_ρ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ) + italic_h ( italic_ρ start_POSTSUBSCRIPT italic_p end_POSTSUBSCRIPT ) .

The conjectured lower bound ( 5 ) is attained for all pure Gaussian states. First, it is immediate to check that it is saturated for the vacuum state, i.e. the Fock state | 0 ⟩ ket 0 \ket{0} | start_ARG 0 end_ARG ⟩ , which is associated with the Wigner function

\mathcal{W}_{+} caligraphic_W start_POSTSUBSCRIPT + end_POSTSUBSCRIPT .

Wigner-Rényi entropy. The Shannon entropy is only a prominent special case of a larger family of entropic functionals called Rényi entropies. Let us first define the p 𝑝 p italic_p -norm of a Wigner function as

1 2 𝒩 𝑊 \|W\|_{1}=1+2\mathcal{N}(W) ∥ italic_W ∥ start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT = 1 + 2 caligraphic_N ( italic_W ) where 𝒩 = ∫ W < 0 | W ⁢ ( α ) | ⁢ d 2 α 𝒩 subscript 𝑊 0 𝑊 𝛼 superscript 2 𝛼 \mathcal{N}=\int_{W<0}\absolutevalue{W(\alpha)}\differential^{2}\alpha caligraphic_N = ∫ start_POSTSUBSCRIPT italic_W < 0 end_POSTSUBSCRIPT | start_ARG italic_W ( italic_α ) end_ARG | start_DIFFOP roman_d end_DIFFOP start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT italic_α . In the limit p → 0 → 𝑝 0 p\rightarrow 0 italic_p → 0 , the p 𝑝 p italic_p -norm is related to the support of W 𝑊 W italic_W and one defines ‖ W ‖ 0 := ν ⁢ ( supp ⁢ ( W ) ) assign subscript norm 𝑊 0 𝜈 supp 𝑊 \|W\|_{0}\vcentcolon=\nu(\mathrm{supp}(W)) ∥ italic_W ∥ start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT := italic_ν ( roman_supp ( italic_W ) ) , where ν 𝜈 \nu italic_ν stands for the Lebesgue measure. Note that Wigner functions always have an infinite support, so ‖ W ‖ 0 subscript norm 𝑊 0 \|W\|_{0} ∥ italic_W ∥ start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT diverges [ 35 ] . In the limit p → ∞ → 𝑝 p\rightarrow\infty italic_p → ∞ , the p 𝑝 p italic_p -norm is related to the maximum absolute value of W 𝑊 W italic_W , and one defines ‖ W ‖ ∞ := max ⁡ | W | assign subscript norm 𝑊 𝑊 \|W\|_{\infty}\vcentcolon=\max\absolutevalue{W} ∥ italic_W ∥ start_POSTSUBSCRIPT ∞ end_POSTSUBSCRIPT := roman_max | start_ARG italic_W end_ARG | . Now that the p 𝑝 p italic_p -norms of a Wigner function have been defined, we are in position to define the Wigner-Rényi entropy.

Definition 2 (Wigner-Rényi entropy [ 16 ] ) .

The Wigner-Rényi entropy of a state ρ ^ ^ 𝜌 \hat{\rho} over^ start_ARG italic_ρ end_ARG is defined as:

Conjecture 2 (Wigner-Rényi entropy conjecture [ 16 ] ) .

The Wigner-Rényi entropy of a Wigner-positive state satisfies the following lower bound:

Just as for the Wigner entropy, the vacuum state saturates the bound since we have

𝜋 1 h(W_{0})=\ln\pi+1 italic_h ( italic_W start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ) = roman_ln italic_π + 1 in the limit α → 1 → 𝛼 1 \alpha\rightarrow 1 italic_α → 1 . The same is true for all pure Gaussian states because h α subscript ℎ 𝛼 h_{\alpha} italic_h start_POSTSUBSCRIPT italic_α end_POSTSUBSCRIPT is invariant under symplectic transformations for all α 𝛼 \alpha italic_α . From this, it is clear that Conjecture  1 is a special case of Conjecture  2 . Recently, it was shown that the Wigner-Rényi entropy satisfies this lower bound for all Wigner-positive states in the regime α ≥ 2 𝛼 2 \alpha\geq 2 italic_α ≥ 2 [ 20 ] , which provides a partial proof of Conjecture 2 (but does not prove Conjecture  1 ).

Lastly, let us mention that a stronger statement implying Conjecture 2 (hence Conjecture  1 ) has also been conjectured that is based on continuous majorization theory. This so-called Wigner majorization conjecture states that the Wigner function of the vacuum W 0 subscript 𝑊 0 W_{0} italic_W start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT continuously majorizes any non-negative Wigner function [ 18 ] .

III Beam-splitter states

𝜂 subscript ^ 𝑎 1 1 𝜂 subscript ^ 𝑎 2 \hat{a}_{1}\mapsto\sqrt{\eta}\hat{a}_{1}+\sqrt{1-\eta}\hat{a}_{2} over^ start_ARG italic_a end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ↦ square-root start_ARG italic_η end_ARG over^ start_ARG italic_a end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT + square-root start_ARG 1 - italic_η end_ARG over^ start_ARG italic_a end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT . In the Schrödinger picture, the action of the beam splitter is appropriately described through a rescaling and a convolution of the Wigner functions.

Let us first define these operations. The rescaling operator ℒ s subscript ℒ 𝑠 \mathcal{L}_{s} caligraphic_L start_POSTSUBSCRIPT italic_s end_POSTSUBSCRIPT acts on a Wigner function as

where s ∈ ℝ > 0 𝑠 subscript ℝ absent 0 s\in\mathbb{R}_{>0} italic_s ∈ blackboard_R start_POSTSUBSCRIPT > 0 end_POSTSUBSCRIPT . For s < 1 𝑠 1 s<1 italic_s < 1 it performs a contraction of W 𝑊 W italic_W towards the origin of phase space; for s > 1 𝑠 1 s>1 italic_s > 1 it performs a dilation. The prefactor ensures that the rescaled function remains normalized. Note that a rescaling may be understood as a change of the constant ℏ Planck-constant-over-2-pi \hbar roman_ℏ (so far assumed to be 1 1 1 1 ), that is, the change ℏ → ℏ ′ → Planck-constant-over-2-pi superscript Planck-constant-over-2-pi ′ \hbar\rightarrow\hbar^{\prime} roman_ℏ → roman_ℏ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT is described by a rescaling ℒ s subscript ℒ 𝑠 \mathcal{L}_{s} caligraphic_L start_POSTSUBSCRIPT italic_s end_POSTSUBSCRIPT where s = ℏ ′ / ℏ 𝑠 superscript Planck-constant-over-2-pi ′ Planck-constant-over-2-pi s=\sqrt{\hbar^{\prime}/\hbar} italic_s = square-root start_ARG roman_ℏ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT / roman_ℏ end_ARG . Second, the convolution of two Wigner functions is defined as:

With these definitions, the action of the beam splitter can be described as follows. The state ρ ^ 1 subscript ^ 𝜌 1 \hat{\rho}_{1} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT and ρ ^ 2 subscript ^ 𝜌 2 \hat{\rho}_{2} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT (with respective Wigner functions W 1 subscript 𝑊 1 W_{1} italic_W start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT and W 2 subscript 𝑊 2 W_{2} italic_W start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) produce the reduced state σ ^ = Tr ⁡ [ U ^ η ⁢ ( ρ ^ 1 ⊗ ρ ^ 2 ) ⁢ U ^ η † ] ^ 𝜎 trace subscript ^ 𝑈 𝜂 tensor-product subscript ^ 𝜌 1 subscript ^ 𝜌 2 subscript superscript ^ 𝑈 † 𝜂 \hat{\sigma}=\Tr[\hat{U}_{\eta}(\hat{\rho}_{1}\otimes\hat{\rho}_{2})\hat{U}^{% \dagger}_{\eta}] over^ start_ARG italic_σ end_ARG = roman_Tr [ over^ start_ARG italic_U end_ARG start_POSTSUBSCRIPT italic_η end_POSTSUBSCRIPT ( over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ⊗ over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) over^ start_ARG italic_U end_ARG start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_η end_POSTSUBSCRIPT ] with Wigner function

𝜂 𝐗 1 𝜂 𝐘 \mathbf{Z}=\sqrt{\eta}\mathbf{X}+\sqrt{1-\eta}\mathbf{Y} bold_Z = square-root start_ARG italic_η end_ARG bold_X + square-root start_ARG 1 - italic_η end_ARG bold_Y ; then we have p 𝐙 = ℒ η ⁢ [ p 𝐗 ] ∗ ℒ 1 − η ⁢ [ p 𝐘 ] subscript 𝑝 𝐙 ∗ subscript ℒ 𝜂 delimited-[] subscript 𝑝 𝐗 subscript ℒ 1 𝜂 delimited-[] subscript 𝑝 𝐘 p_{\mathbf{Z}}=\mathcal{L}_{\sqrt{\eta}}[p_{\mathbf{X}}]\ast\mathcal{L}_{\sqrt% {1-\eta}}[p_{\mathbf{Y}}] italic_p start_POSTSUBSCRIPT bold_Z end_POSTSUBSCRIPT = caligraphic_L start_POSTSUBSCRIPT square-root start_ARG italic_η end_ARG end_POSTSUBSCRIPT [ italic_p start_POSTSUBSCRIPT bold_X end_POSTSUBSCRIPT ] ∗ caligraphic_L start_POSTSUBSCRIPT square-root start_ARG 1 - italic_η end_ARG end_POSTSUBSCRIPT [ italic_p start_POSTSUBSCRIPT bold_Y end_POSTSUBSCRIPT ] .

The convolution of two Wigner functions W 1 ∗ W 2 ∗ subscript 𝑊 1 subscript 𝑊 2 W_{1}\ast W_{2} italic_W start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ∗ italic_W start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT is always non-negative [ 37 , 38 , 39 ] . Hence, if we choose the transmittance of the beam splitter to be η = 1 / 2 𝜂 1 2 \eta=1/2 italic_η = 1 / 2 , Eq. ( 13 ) becomes W σ = ℒ 1 / 2 ⁢ [ W 1 ∗ W 2 ] subscript 𝑊 𝜎 subscript ℒ 1 2 delimited-[] ∗ subscript 𝑊 1 subscript 𝑊 2 \smash{W_{\sigma}=\mathcal{L}_{1/\sqrt{2}}[W_{1}\ast W_{2}]} italic_W start_POSTSUBSCRIPT italic_σ end_POSTSUBSCRIPT = caligraphic_L start_POSTSUBSCRIPT 1 / square-root start_ARG 2 end_ARG end_POSTSUBSCRIPT [ italic_W start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ∗ italic_W start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ] which is a non-negative Wigner function. This setup producing Wigner-positive states is depicted in Fig.  2 . We have restricted to inputs of the product form ρ ^ 1 ⊗ ρ ^ 2 tensor-product subscript ^ 𝜌 1 subscript ^ 𝜌 2 \hat{\rho}_{1}\otimes\hat{\rho}_{2} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ⊗ over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT , but observe that any separable input state (i.e., convex mixture of product states) also produces a Wigner-positive state in this setup since a convex mixture of Wigner-positive states is Wigner positive. This leads us to define the set of beam-splitter (BS) states, which we denote as ℬ ℬ \mathcal{B} caligraphic_B 3 3 3 Note the discrepancy with the notation used in Ref.  [ 16 ] , where ℬ ℬ \mathcal{B} caligraphic_B denotes the subset of states σ ^ ⁢ ( ρ ^ 1 , ρ ^ 2 ) ^ 𝜎 subscript ^ 𝜌 1 subscript ^ 𝜌 2 \hat{\sigma}(\hat{\rho}_{1},\hat{\rho}_{2}) over^ start_ARG italic_σ end_ARG ( over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) whereas ℬ c subscript ℬ 𝑐 \mathcal{B}_{c} caligraphic_B start_POSTSUBSCRIPT italic_c end_POSTSUBSCRIPT denotes the closure of its convex hull. .

Definition 3 (Beam-splitter state) .

A BS state is any state σ ^ ^ 𝜎 \hat{\sigma} over^ start_ARG italic_σ end_ARG that can be obtained as the single-mode output of a balanced beam splitter acting on a separable input ρ ^ sep subscript ^ 𝜌 sep \hat{\rho}_{\mathrm{sep}} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT roman_sep end_POSTSUBSCRIPT , i.e.

In the following, we also use the shorthand notation

when refering to the BS states produced by the product states ρ ^ 1 ⊗ ρ ^ 2 tensor-product subscript ^ 𝜌 1 subscript ^ 𝜌 2 \hat{\rho}_{1}\otimes\hat{\rho}_{2} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ⊗ over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT . Note that in the special case where ρ ^ 1 = ρ ^ 2 = ρ ^ G subscript ^ 𝜌 1 subscript ^ 𝜌 2 subscript ^ 𝜌 𝐺 \hat{\rho}_{1}=\hat{\rho}_{2}=\hat{\rho}_{G} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT = over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT = over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT , with ρ ^ G subscript ^ 𝜌 𝐺 \hat{\rho}_{G} over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT being an arbitrary Gaussian state, it is well known that σ ^ ⁢ ( ρ ^ G , ρ ^ G ) = ρ ^ G ^ 𝜎 subscript ^ 𝜌 𝐺 subscript ^ 𝜌 𝐺 subscript ^ 𝜌 𝐺 \hat{\sigma}(\hat{\rho}_{G},\hat{\rho}_{G})=\hat{\rho}_{G} over^ start_ARG italic_σ end_ARG ( over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT , over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT ) = over^ start_ARG italic_ρ end_ARG start_POSTSUBSCRIPT italic_G end_POSTSUBSCRIPT , implying that Gaussian states (and any mixture thereof) are included in the set ℬ ℬ \mathcal{B} caligraphic_B of BS states, hence Gaussian states are obviously Wigner positive.

\mathcal{B}\subset\mathcal{W}_{+} caligraphic_B ⊂ caligraphic_W start_POSTSUBSCRIPT + end_POSTSUBSCRIPT [ 16 ] , hence our proof is not yet a full proof of Conjecture 1 .

Subset of elementary BS states. Within the set ℬ ℬ \mathcal{B} caligraphic_B , we identify the subset of BS states that are produced by pure separable (product) states, which we call elementary BS states and denote with a ∗ ∗ \ast ∗ -subscript. They are defined as

and their associated Wigner functions are written as