Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Inferential Statistics | An Easy Introduction & Examples

Inferential Statistics | An Easy Introduction & Examples
Published on September 4, 2020 by Pritha Bhandari . Revised on June 22, 2023.
While descriptive statistics summarize the characteristics of a data set, inferential statistics help you come to conclusions and make predictions based on your data.
When you have collected data from a sample , you can use inferential statistics to understand the larger population from which the sample is taken.
Inferential statistics have two main uses:
- making estimates about populations (for example, the mean SAT score of all 11th graders in the US).
- testing hypotheses to draw conclusions about populations (for example, the relationship between SAT scores and family income).
Table of contents
Descriptive versus inferential statistics, estimating population parameters from sample statistics, hypothesis testing, other interesting articles, frequently asked questions about inferential statistics.
Descriptive statistics allow you to describe a data set, while inferential statistics allow you to make inferences based on a data set.
- Descriptive statistics
Using descriptive statistics, you can report characteristics of your data:
- The distribution concerns the frequency of each value.
- The central tendency concerns the averages of the values.
- The variability concerns how spread out the values are.
In descriptive statistics, there is no uncertainty – the statistics precisely describe the data that you collected. If you collect data from an entire population, you can directly compare these descriptive statistics to those from other populations.
Inferential statistics
Most of the time, you can only acquire data from samples, because it is too difficult or expensive to collect data from the whole population that you’re interested in.
While descriptive statistics can only summarize a sample’s characteristics, inferential statistics use your sample to make reasonable guesses about the larger population.
With inferential statistics, it’s important to use random and unbiased sampling methods . If your sample isn’t representative of your population, then you can’t make valid statistical inferences or generalize .
Sampling error in inferential statistics
Since the size of a sample is always smaller than the size of the population, some of the population isn’t captured by sample data. This creates sampling error , which is the difference between the true population values (called parameters) and the measured sample values (called statistics).
Sampling error arises any time you use a sample, even if your sample is random and unbiased. For this reason, there is always some uncertainty in inferential statistics. However, using probability sampling methods reduces this uncertainty.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The characteristics of samples and populations are described by numbers called statistics and parameters :
- A statistic is a measure that describes the sample (e.g., sample mean ).
- A parameter is a measure that describes the whole population (e.g., population mean).
Sampling error is the difference between a parameter and a corresponding statistic. Since in most cases you don’t know the real population parameter, you can use inferential statistics to estimate these parameters in a way that takes sampling error into account.
There are two important types of estimates you can make about the population: point estimates and interval estimates .
- A point estimate is a single value estimate of a parameter. For instance, a sample mean is a point estimate of a population mean.
- An interval estimate gives you a range of values where the parameter is expected to lie. A confidence interval is the most common type of interval estimate.
Both types of estimates are important for gathering a clear idea of where a parameter is likely to lie.
Confidence intervals
A confidence interval uses the variability around a statistic to come up with an interval estimate for a parameter. Confidence intervals are useful for estimating parameters because they take sampling error into account.
While a point estimate gives you a precise value for the parameter you are interested in, a confidence interval tells you the uncertainty of the point estimate. They are best used in combination with each other.
Each confidence interval is associated with a confidence level. A confidence level tells you the probability (in percentage) of the interval containing the parameter estimate if you repeat the study again.
A 95% confidence interval means that if you repeat your study with a new sample in exactly the same way 100 times, you can expect your estimate to lie within the specified range of values 95 times.
Although you can say that your estimate will lie within the interval a certain percentage of the time, you cannot say for sure that the actual population parameter will. That’s because you can’t know the true value of the population parameter without collecting data from the full population.
However, with random sampling and a suitable sample size, you can reasonably expect your confidence interval to contain the parameter a certain percentage of the time.
Your point estimate of the population mean paid vacation days is the sample mean of 19 paid vacation days.
Hypothesis testing is a formal process of statistical analysis using inferential statistics. The goal of hypothesis testing is to compare populations or assess relationships between variables using samples.
Hypotheses , or predictions, are tested using statistical tests . Statistical tests also estimate sampling errors so that valid inferences can be made.
Statistical tests can be parametric or non-parametric. Parametric tests are considered more statistically powerful because they are more likely to detect an effect if one exists.
Parametric tests make assumptions that include the following:
- the population that the sample comes from follows a normal distribution of scores
- the sample size is large enough to represent the population
- the variances , a measure of variability , of each group being compared are similar
When your data violates any of these assumptions, non-parametric tests are more suitable. Non-parametric tests are called “distribution-free tests” because they don’t assume anything about the distribution of the population data.
Statistical tests come in three forms: tests of comparison, correlation or regression.
Comparison tests
Comparison tests assess whether there are differences in means, medians or rankings of scores of two or more groups.
To decide which test suits your aim, consider whether your data meets the conditions necessary for parametric tests, the number of samples, and the levels of measurement of your variables.
Means can only be found for interval or ratio data , while medians and rankings are more appropriate measures for ordinal data .
| test | Yes | Means | 2 samples |
|---|---|---|---|
| Yes | Means | 3+ samples | |
| Mood’s median | No | Medians | 2+ samples |
| Wilcoxon signed-rank | No | Distributions | 2 samples |
| Wilcoxon rank-sum (Mann-Whitney ) | No | Sums of rankings | 2 samples |
| Kruskal-Wallis | No | Mean rankings | 3+ samples |
Correlation tests
Correlation tests determine the extent to which two variables are associated.
Although Pearson’s r is the most statistically powerful test, Spearman’s r is appropriate for interval and ratio variables when the data doesn’t follow a normal distribution.
The chi square test of independence is the only test that can be used with nominal variables.
| Pearson’s | Yes | Interval/ratio variables |
|---|---|---|
| Spearman’s | No | Ordinal/interval/ratio variables |
| Chi square test of independence | No | Nominal/ordinal variables |
Regression tests
Regression tests demonstrate whether changes in predictor variables cause changes in an outcome variable. You can decide which regression test to use based on the number and types of variables you have as predictors and outcomes.
Most of the commonly used regression tests are parametric. If your data is not normally distributed, you can perform data transformations.
Data transformations help you make your data normally distributed using mathematical operations, like taking the square root of each value.
| 1 interval/ratio variable | 1 interval/ratio variable | |
| 2+ interval/ratio variable(s) | 1 interval/ratio variable | |
| Logistic regression | 1+ any variable(s) | 1 binary variable |
| Nominal regression | 1+ any variable(s) | 1 nominal variable |
| Ordinal regression | 1+ any variable(s) | 1 ordinal variable |
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Confidence interval
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Prevent plagiarism. Run a free check.
Descriptive statistics summarize the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalizable to the broader population.
A statistic refers to measures about the sample , while a parameter refers to measures about the population .
A sampling error is the difference between a population parameter and a sample statistic .
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). Inferential Statistics | An Easy Introduction & Examples. Scribbr. Retrieved August 28, 2024, from https://www.scribbr.com/statistics/inferential-statistics/
Is this article helpful?

Pritha Bhandari
Other students also liked, parameter vs statistic | definitions, differences & examples, descriptive statistics | definitions, types, examples, hypothesis testing | a step-by-step guide with easy examples, what is your plagiarism score.

An Introduction to Inferential Analysis in Qualitative Research
January 10, 2021
By Aidan Gray

When conducting qualitative research, an researcher may adopt an inferential or deductive approach. For example, research questionnaires are primarily used as a means to obtain data on customer satisfaction or level of knowledge about a particular topic. The questionnaires themselves are not necessarily qualitative, but are descriptive of a given set of facts (usually referred to as “observational data” or “subjective data”). However, the questionnaires are designed to answer specific questions that will provide the researcher with data to support a central claim. If the data does not support the claimed conclusion, then the researcher should reject the theory, but if the data does support the conclusion, the researcher should use that conclusion to support a thesis.
Research theories, however, are not a pure, monolithic category. They can be of many different types. In research methodology, the theories are descriptive and predictive of the actual empirical results of research efforts. When this is done, the researcher is said to have conducted a “lull theory”, in reference to the fact that when people are at a relaxed state, their answers tend to reflect reality more closely than answers they would give while at work or in school.
Another type of theory in research methodology is descriptive data theory. This refers to methods of testing a hypothesis by examining a large number of the facts that are independent of the original study and using those facts to construct a hypothesis about the original data. More specifically, this would be used to test the generalizability of the theory. It is often called a falsification theory because it attempts to verify the original hypothesis.
Another method called measurement theory is popularly used in research methodology. It is best explained as a way to test the generalizability of a research method. The purpose of measuring is to provide quantitative proof that the original, descriptive method is sound. For instance, a researcher conducting an experiment may choose to use a t-test or a chi-square test. Both of these methods are considered to be valid testing methods when compared to null results.
Inferential Approach In Research
Another important tool used in qualitative research is questionnaires. These questionnaires allow a researcher to obtain information from a large number of people, many of which are likely non-relevant to the topic being investigated. For example, a survey might be designed to investigate the relationships between smoking and weight. In this case, the questions would likely address things like demographics, beliefs about smoking and weight and various other factors that directly affect smoking prevalence. Questionnaires can also be used to investigate if certain behaviors affect people in different ways and to find out if there is consistency within groups concerning those behaviors.
Most research questionnaires, however, fall under the more descriptive category. These questionnaires are designed to gather data that will support the main topic of the research. Some examples include surveys on organizational behavior, attitudes toward sexuality and the HIV epidemic among others. These questionnaires are also typically longer than those used in clinical research. For example, an organizational survey might last up to 8 pages while a questionnaire for a clinical trial could be lengthy as well as drawn from a variety of sources.
Other forms of quantitative research rely heavily on descriptive analysis and statistical measures. For example, studies about student drinking and driving have to make sure that they have appropriate sampling tools and that their questionnaires and methodology are accurate. Demographics must be collected to accurately determine where the focus of a given study fits within a population. This type of research can also depend heavily on the use of statistical measures and analysis.
When a qualitative researcher resorts to the inferential approach, they generally are doing so because they do not have an exact idea of the answer that would result from a directed question or a graphical representation. The inferential approach allows them to infer a probability based on the information that is available to them. In most cases, the researcher uses statistical methods and data to come to a conclusion. If they choose to rely solely on the descriptive aspects of the topic they are researching, then they are limiting their potential to provide quantitative proof. Qualitative researchers must then follow certain rules in order to use statistics and other empirical measures in a way that helps them draw conclusions about a topic.
- Recent Posts
- IVR Optimization Strategies - July 17, 2024
- Custom React JS Development for Enterprises - July 12, 2024
- The Role of Photochemistry Reactors in Chemical Reactions - May 7, 2024
Continue Reading
- What Is Simulation Analysis in Finance?
- Risk Management - How to Apply Simulation Analysis in Risk Management
- What Is Simulation Theory?
- The Importance of Software Simulation Examples
- Examples of Scenario Analysis Examples
Privacy Overview
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
- Privacy Policy

Home » Inferential Statistics – Types, Methods and Examples
Inferential Statistics – Types, Methods and Examples
Table of Contents

Inferential Statistics
Inferential statistics is a branch of statistics that involves making predictions or inferences about a population based on a sample of data taken from that population. It is used to analyze the probabilities, assumptions, and outcomes of a hypothesis .
The basic steps of inferential statistics typically involve the following:
- Define a Hypothesis: This is often a statement about a parameter of a population, such as the population mean or population proportion.
- Select a Sample: In order to test the hypothesis, you’ll select a sample from the population. This should be done randomly and should be representative of the larger population in order to avoid bias.
- Collect Data: Once you have your sample, you’ll need to collect data. This data will be used to calculate statistics that will help you test your hypothesis.
- Perform Analysis: The collected data is then analyzed using statistical tests such as the t-test, chi-square test, or ANOVA, to name a few. These tests help to determine the likelihood that the results of your analysis occurred by chance.
- Interpret Results: The analysis can provide a probability, called a p-value, which represents the likelihood that the results occurred by chance. If this probability is below a certain level (commonly 0.05), you may reject the null hypothesis (the statement that there is no effect or relationship) in favor of the alternative hypothesis (the statement that there is an effect or relationship).
Inferential Statistics Types
Inferential statistics can be broadly categorized into two types: parametric and nonparametric. The selection of type depends on the nature of the data and the purpose of the analysis.
Parametric Inferential Statistics
These are statistical methods that assume data comes from a type of probability distribution and makes inferences about the parameters of the distribution. Common parametric methods include:
- T-tests : Used when comparing the means of two groups to see if they’re significantly different.
- Analysis of Variance (ANOVA) : Used to compare the means of more than two groups.
- Regression Analysis : Used to predict the value of one variable (dependent) based on the value of another variable (independent).
- Chi-square test for independence : Used to test if there is a significant association between two categorical variables.
- Pearson’s correlation : Used to test if there is a significant linear relationship between two continuous variables.
Nonparametric Inferential Statistics
These are methods used when the data does not meet the requirements necessary to use parametric statistics, such as when data is not normally distributed. Common nonparametric methods include:
- Mann-Whitney U Test : Non-parametric equivalent to the independent samples t-test.
- Wilcoxon Signed-Rank Test : Non-parametric equivalent to the paired samples t-test.
- Kruskal-Wallis Test : Non-parametric equivalent to the one-way ANOVA.
- Spearman’s rank correlation : Non-parametric equivalent to the Pearson correlation.
- Chi-square test for goodness of fit : Used to test if the observed frequencies for a categorical variable match the expected frequencies.
Inferential Statistics Formulas
Inferential statistics use various formulas and statistical tests to draw conclusions or make predictions about a population based on a sample from that population. Here are a few key formulas commonly used:
Confidence Interval for a Mean:
When you have a sample and want to make an inference about the population mean (µ), you might use a confidence interval.
The formula for a confidence interval around a mean is:
[Sample Mean] ± [Z-score or T-score] * (Standard Deviation / sqrt[n]) where:
- Sample Mean is the mean of your sample data
- Z-score or T-score is the value from the Z or T distribution corresponding to the desired confidence level (Z is used when the population standard deviation is known or the sample size is large, otherwise T is used)
- Standard Deviation is the standard deviation of the sample
- sqrt[n] is the square root of the sample size
Hypothesis Testing:
Hypothesis testing often involves calculating a test statistic, which is then compared to a critical value to decide whether to reject the null hypothesis.
A common test statistic for a test about a mean is the Z-score:
Z = (Sample Mean - Hypothesized Population Mean) / (Standard Deviation / sqrt[n])
where all variables are as defined above.
Chi-Square Test:
The Chi-Square Test is used when dealing with categorical data.
The formula is:
χ² = Σ [ (Observed-Expected)² / Expected ]
- Observed is the actual observed frequency
- Expected is the frequency we would expect if the null hypothesis were true
The t-test is used to compare the means of two groups. The formula for the independent samples t-test is:
t = (mean1 - mean2) / sqrt [ (sd1²/n1) + (sd2²/n2) ] where:
- mean1 and mean2 are the sample means
- sd1 and sd2 are the sample standard deviations
- n1 and n2 are the sample sizes
Inferential Statistics Examples
Sure, inferential statistics are used when making predictions or inferences about a population from a sample of data. Here are a few real-time examples:
- Medical Research: Suppose a pharmaceutical company is developing a new drug and they’re currently in the testing phase. They gather a sample of 1,000 volunteers to participate in a clinical trial. They find that 700 out of these 1,000 volunteers reported a significant reduction in their symptoms after taking the drug. Using inferential statistics, they can infer that the drug would likely be effective for the larger population.
- Customer Satisfaction: Suppose a restaurant wants to know if its customers are satisfied with their food. They could survey a sample of their customers and ask them to rate their satisfaction on a scale of 1 to 10. If the average rating was 8.5 from a sample of 200 customers, they could use inferential statistics to infer that the overall customer population is likely satisfied with the food.
- Political Polling: A polling company wants to predict who will win an upcoming presidential election. They poll a sample of 10,000 eligible voters and find that 55% prefer Candidate A, while 45% prefer Candidate B. Using inferential statistics, they infer that Candidate A has a higher likelihood of winning the election.
- E-commerce Trends: An e-commerce company wants to improve its recommendation engine. They analyze a sample of customers’ purchase history and notice a trend that customers who buy kitchen appliances also frequently buy cookbooks. They use inferential statistics to infer that recommending cookbooks to customers who buy kitchen appliances would likely increase sales.
- Public Health: A health department wants to assess the impact of a health awareness campaign on smoking rates. They survey a sample of residents before and after the campaign. If they find a significant reduction in smoking rates among the surveyed group, they can use inferential statistics to infer that the campaign likely had an impact on the larger population’s smoking habits.
Applications of Inferential Statistics
Inferential statistics are extensively used in various fields and industries to make decisions or predictions based on data. Here are some applications of inferential statistics:
- Healthcare: Inferential statistics are used in clinical trials to analyze the effect of a treatment or a drug on a sample population and then infer the likely effect on the general population. This helps in the development and approval of new treatments and drugs.
- Business: Companies use inferential statistics to understand customer behavior and preferences, market trends, and to make strategic decisions. For example, a business might sample customer satisfaction levels to infer the overall satisfaction of their customer base.
- Finance: Banks and financial institutions use inferential statistics to evaluate the risk associated with loans and investments. For example, inferential statistics can help in determining the risk of default by a borrower based on the analysis of a sample of previous borrowers with similar credit characteristics.
- Quality Control: In manufacturing, inferential statistics can be used to maintain quality standards. By analyzing a sample of the products, companies can infer the quality of all products and decide whether the manufacturing process needs adjustments.
- Social Sciences: In fields like psychology, sociology, and education, researchers use inferential statistics to draw conclusions about populations based on studies conducted on samples. For instance, a psychologist might use a survey of a sample of people to infer the prevalence of a particular psychological trait or disorder in a larger population.
- Environment Studies: Inferential statistics are also used to study and predict environmental changes and their impact. For instance, researchers might measure pollution levels in a sample of locations to infer overall pollution levels in a wider area.
- Government Policies: Governments use inferential statistics in policy-making. By analyzing sample data, they can infer the potential impacts of policies on the broader population and thus make informed decisions.
Purpose of Inferential Statistics
The purposes of inferential statistics include:
- Estimation of Population Parameters: Inferential statistics allows for the estimation of population parameters. This means that it can provide estimates about population characteristics based on sample data. For example, you might want to estimate the average weight of all men in a country by sampling a smaller group of men.
- Hypothesis Testing: Inferential statistics provides a framework for testing hypotheses. This involves making an assumption (the null hypothesis) and then testing this assumption to see if it should be rejected or not. This process enables researchers to draw conclusions about population parameters based on their sample data.
- Prediction: Inferential statistics can be used to make predictions about future outcomes. For instance, a researcher might use inferential statistics to predict the outcomes of an election or forecast sales for a company based on past data.
- Relationships Between Variables: Inferential statistics can also be used to identify relationships between variables, such as correlation or regression analysis. This can provide insights into how different factors are related to each other.
- Generalization: Inferential statistics allows researchers to generalize their findings from the sample to the larger population. It helps in making broad conclusions, given that the sample is representative of the population.
- Variability and Uncertainty: Inferential statistics also deal with the idea of uncertainty and variability in estimates and predictions. Through concepts like confidence intervals and margins of error, it provides a measure of how confident we can be in our estimations and predictions.
- Error Estimation : It provides measures of possible errors (known as margins of error), which allow us to know how much our sample results may differ from the population parameters.
Limitations of Inferential Statistics
Inferential statistics, despite its many benefits, does have some limitations. Here are some of them:
- Sampling Error : Inferential statistics are often based on the concept of sampling, where a subset of the population is used to infer about the population. There’s always a chance that the sample might not perfectly represent the population, leading to sampling errors.
- Misleading Conclusions : If assumptions for statistical tests are not met, it could lead to misleading results. This includes assumptions about the distribution of data, homogeneity of variances, independence, etc.
- False Positives and Negatives : There’s always a chance of a Type I error (rejecting a true null hypothesis, or a false positive) or a Type II error (not rejecting a false null hypothesis, or a false negative).
- Dependence on Quality of Data : The accuracy and validity of inferential statistics depend heavily on the quality of data collected. If data are biased, inaccurate, or collected using flawed methods, the results won’t be reliable.
- Limited Predictive Power : While inferential statistics can provide estimates and predictions, these are based on the current data and may not fully account for future changes or variables not included in the model.
- Complexity : Some inferential statistical methods can be quite complex and require a solid understanding of statistical principles to implement and interpret correctly.
- Influenced by Outliers : Inferential statistics can be heavily influenced by outliers. If these extreme values aren’t handled properly, they can lead to misleading results.
- Over-reliance on P-values : There’s a tendency in some fields to overly rely on p-values to determine significance, even though p-values have several limitations and are often misunderstood.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Textual Analysis – Types, Examples and Guide

Discourse Analysis – Methods, Types and Examples

Grounded Theory – Methods, Examples and Guide

Narrative Analysis – Types, Methods and Examples

Regression Analysis – Methods, Types and Examples

Histogram – Types, Examples and Making Guide

Quant Analysis 101: Inferential Statistics
Everything You Need To Get Started (With Examples)
By: Derek Jansen (MBA) | Reviewers: Kerryn Warren (PhD) | October 2023
If you’re new to quantitative data analysis , one of the many terms you’re likely to hear being thrown around is inferential statistics. In this post, we’ll provide an introduction to inferential stats, using straightforward language and loads of examples .
Overview: Inferential Statistics
What are inferential statistics.
- Descriptive vs inferential statistics
Correlation
- Key takeaways
At the simplest level, inferential statistics allow you to test whether the patterns you observe in a sample are likely to be present in the population – or whether they’re just a product of chance.
In stats-speak, this “Is it real or just by chance?” assessment is known as statistical significance . We won’t go down that rabbit hole in this post, but this ability to assess statistical significance means that inferential statistics can be used to test hypotheses and in some cases, they can even be used to make predictions .
That probably sounds rather conceptual – let’s look at a practical example.
Let’s say you surveyed 100 people (this would be your sample) in a specific city about their favourite type of food. Reviewing the data, you found that 70 people selected pizza (i.e., 70% of the sample). You could then use inferential statistics to test whether that number is just due to chance , or whether it is likely representative of preferences across the entire city (this would be your population).
PS – you’d use a chi-square test for this example, but we’ll get to that a little later.

Inferential vs Descriptive
At this point, you might be wondering how inferentials differ from descriptive statistics. At the simplest level, descriptive statistics summarise and organise the data you already have (your sample), making it easier to understand.
Inferential statistics, on the other hand, allow you to use your sample data to assess whether the patterns contained within it are likely to be present in the broader population , and potentially, to make predictions about that population.
It’s example time again…
Let’s imagine you’re undertaking a study that explores shoe brand preferences among men and women. If you just wanted to identify the proportions of those who prefer different brands, you’d only require descriptive statistics .
However, if you wanted to assess whether those proportions differ between genders in the broader population (and that the difference is not just down to chance), you’d need to utilise inferential statistics .
In short, descriptive statistics describe your sample, while inferential statistics help you understand whether the patterns in your sample are likely to reflect within the population .

Let’s look at some inferential tests
Now that we’ve defined inferential statistics and explained how it differs from descriptive statistics, let’s take a look at some of the most common tests within the inferential realm . It’s worth highlighting upfront that there are many different types of inferential tests and this is most certainly not a comprehensive list – just an introductory list to get you started.
A t-test is a way to compare the means (averages) of two groups to see if they are meaningfully different, or if the difference is just by chance. In other words, to assess whether the difference is statistically significant . This is important because comparing two means side-by-side can be very misleading if one has a high variance and the other doesn’t (if this sounds like gibberish, check out our descriptive statistics post here ).
As an example, you might use a t-test to see if there’s a statistically significant difference between the exam scores of two mathematics classes taught by different teachers . This might then lead you to infer that one teacher’s teaching method is more effective than the other.
It’s worth noting that there are a few different types of t-tests . In this example, we’re referring to the independent t-test , which compares the means of two groups, as opposed to the mean of one group at different times (i.e., a paired t-test). Each of these tests has its own set of assumptions and requirements, as do all of the tests we’ll discuss here – but we’ll save assumptions for another post!

While a t-test compares the means of just two groups, an ANOVA (which stands for Analysis of Variance) can compare the means of more than two groups at once . Again, this helps you assess whether the differences in the means are statistically significant or simply a product of chance.
For example, if you want to know whether students’ test scores vary based on the type of school they attend – public, private, or homeschool – you could use ANOVA to compare the average standardised test scores of the three groups .
Similarly, you could use ANOVA to compare the average sales of a product across multiple stores. Based on this data, you could make an inference as to whether location is related to (affects) sales.
In these examples, we’re specifically referring to what’s called a one-way ANOVA , but as always, there are multiple types of ANOVAs for different applications. So, be sure to do your research before opting for any specific test.

While t-tests and ANOVAs test for differences in the means across groups, the Chi-square test is used to see if there’s a difference in the proportions of various categories . In stats speak, the Chi-square test assesses whether there’s a statistically significant relationship between two categorical variables (i.e., nominal or ordinal data). If you’re not familiar with these terms, check out our explainer video here .
As an example, you could use a Chi-square test to check if there’s a link between gender (e.g., male and female) and preference for a certain category of car (e.g., sedans or SUVs). Similarly, you could use this type of test to see if there’s a relationship between the type of breakfast people eat (cereal, toast, or nothing) and their university major (business, math or engineering).
Correlation analysis looks at the relationship between two numerical variables (like height or weight) to assess whether they “move together” in some way. In stats-speak, correlation assesses whether a statistically significant relationship exists between two variables that are interval or ratio in nature .
For example, you might find a correlation between hours spent studying and exam scores. This would suggest that generally, the more hours people spend studying, the higher their scores are likely to be.
Similarly, a correlation analysis may reveal a negative relationship between time spent watching TV and physical fitness (represented by VO2 max levels), where the more time spent in front of the television, the lower the physical fitness level.
When running a correlation analysis, you’ll be presented with a correlation coefficient (also known as an r-value), which is a number between -1 and 1. A value close to 1 means that the two variables move in the same direction , while a number close to -1 means that they move in opposite directions . A correlation value of zero means there’s no clear relationship between the two variables.
What’s important to highlight here is that while correlation analysis can help you understand how two variables are related, it doesn’t prove that one causes the other . As the adage goes, correlation is not causation.

While correlation allows you to see whether there’s a relationship between two numerical variables, regression takes it a step further by allowing you to make predictions about the value of one variable (called the dependent variable) based on the value of one or more other variables (called the independent variables).
For example, you could use regression analysis to predict house prices based on the number of bedrooms, location, and age of the house. The analysis would give you an equation that lets you plug in these factors to estimate a house’s price. Similarly, you could potentially use regression analysis to predict a person’s weight based on their height, age, and daily calorie intake.
It’s worth noting that in these examples, we’ve been talking about multiple regression , as there are multiple independent variables. While this is a popular form of regression, there are many others, including simple linear, logistic and multivariate. As always, be sure to do your research before selecting a specific statistical test.
As with correlation, keep in mind that regression analysis alone doesn’t prove causation . While it can show that variables are related and help you make predictions, it can’t prove that one variable causes another to change. Other factors that you haven’t included in your model could be influencing the results. To establish causation, you’d typically need a very specific research design that allows you to control all (or at least most) variables.
Let’s Recap
We’ve covered quite a bit of ground. Here’s a quick recap of the key takeaways:
- Inferential stats allow you to assess whether patterns in your sample are likely to be present in your population
- Some common inferential statistical tests include t-tests, ANOVA, chi-square, correlation and regression .
- Inferential statistics alone do not prove causation . To identify and measure causal relationships, you need a very specific research design.
If you’d like 1-on-1 help with your inferential statistics, check out our private coaching service , where we hold your hand throughout the quantitative research process.

Psst… there’s more!
This post is an extract from our bestselling short course, Methodology Bootcamp . If you want to work smart, you don't want to miss this .
very important content
Submit a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Print Friendly

Research Methods in Psychology
14. inferential statistics ¶.
The great tragedy of science - the slaying of a beautiful hypothesis by an ugly fact. —Thomas Huxley
Truth in science can be defined as the working hypothesis best suited to open the way to the next better one. —Konrad Lorenz
Recall that Matthias Mehl and his colleagues, in their study of sex differences in talkativeness, found that the women in their sample spoke a mean of 16,215 words per day and the men a mean of 15,669 words per day [MVRamirezE+07] . But despite observing this difference in their sample, they concluded that there was no evidence of a sex difference in talkativeness in the population. Recall also that Allen Kanner and his colleagues, in their study of the relationship between daily hassles and symptoms, found a correlation of 0.6 in their sample [KCSL81] . But they concluded that this finding implied a relationship between hassles and symptoms in the population. These examples raise questions about how researchers can draw conclusions about the population based on results from their sample.
To answer such questions, researchers use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research. We begin with a conceptual overview of null hypothesis testing, including its purpose and basic logic. Then we look at several null hypothesis testing techniques that allow conclusions about differences between means and about correlations between quantitative variables. Finally, we consider a few other important ideas related to null hypothesis testing, including some that can be helpful in planning new studies and interpreting results. We also look at some long-standing criticisms of null hypothesis testing and some ways of dealing with these criticisms.
14.1. Understanding Null Hypothesis Testing ¶
14.1.1. learning objectives ¶.
Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
14.1.2. The Purpose of Null Hypothesis Testing ¶
As we have seen, psychological research typically involves measuring one or more variables within a sample and computing descriptive statistics. In general, however, the researcher’s goal is not to draw conclusions about the participants in that sample, but rather to draw conclusions about the population from which those participants were selected. Thus, researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters. Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third. This will happen even though these samples are randomly selected from the same population. Similarly, the correlation (e.g., Pearson’s r) between two variables might be 0.24 in one sample, -0.04 in a second sample, and 0.15 in a third. Again, this can and will happen even though these samples are selected randomly from the same population. This random variability in statistics calculated from sample to sample is called sampling error. Note that the term error here refers to the statistical notion of error, or random variability, and does not imply that anyone has made a mistake. No one “commits a sampling error”.
One implication of this is that when there is a statistical relationship in a sample, it is not always clear whether there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of -0.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any relationship observed in a sample can be interpreted in two ways:
There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of inferential statistics is simply to help researchers decide between these two interpretations.
14.1.3. The Logic of Null Hypothesis Testing ¶
Null hypothesis testing (or NHST) is a formal approach to making decisions between these two interpretations. One interpretation is called the null hypothesis (often symbolized \(H_0\) and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance”. The other interpretation is called the alternative hypothesis (often symbolized as \(H_1\) ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis.
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A small value of p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A large value of p means that the sample result would be likely if the null hypothesis were true and leads the null hypothesis to be accepted. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called \(\alpha\) (alpha) and is often set to .05. If the chance of a result as extreme as the sample result (or more extreme) is less than a 5% if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant. If the chance of of a result as extreme as the sample result is greater than 5% when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true. It means that there is not currently enough evidence to conclude that it is false. For this reason, researchers often use the expression “fail to reject the null hypothesis” rather than something such as “conclude the null hypothesis is true”.
14.1.4. The Misunderstood p Value ¶
The p value is one of the most misunderstood quantities in psychological research [Coh94] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true or that the that the p value is the probability that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect. The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.
14.1.5. Role of Sample Size and Relationship Strength ¶
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” As we have just seen, this question is equivalent to, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Figure 14.1: shows a rough guideline of how relationship strength and sample size might combine to determine whether a sample result is statistically significant or not. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus, each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes, then this combination would be statistically significant for both Cohen’s d and Pearson’s r. If it contains the word No, then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed below, in the section entitled, “Some Basic Null Hypothesis Tests”.
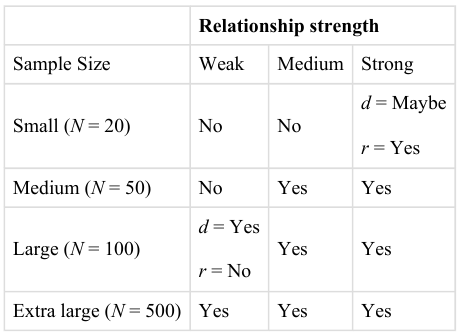
Fig. 14.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant ¶
Although Figure 14.1: provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are less likely to be statistically significant and that strong relationships based on medium or larger samples are more likely to be statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you may need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach.
14.1.6. Statistical Significance Versus Practical Significance ¶
Figure 14.1: illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences [Hyd07] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word “significant” can cause people to interpret these differences as strong and important, perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak, perhaps even “trivial”.
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant (and may even be interesting for purely scientific reasons) but they are often not practically significant. In clinical practice, this same concept is often referred to as “clinical significance”. For example, a study on a new treatment for social phobia might show that it produces a positive effect that is statistically significant. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice. For example, easier and cheaper treatments that work almost as well might already exist. Although statistically significant, this result would be said to lack practical or clinical significance.
14.1.7. Key Takeaways ¶
Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
14.1.8. Exercises ¶
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
Practice: Use Figure 14.1: to try and determine whether each of the following results is statistically significant:
a. The correlation between two variables is r = -0.78 based on a sample size of 137.
b. The mean score on a psychological characteristic for women is 25 (SD = 5) and the mean score for men is 24 (SD = 5). There were 12 women and 10 men in this study.
c. In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
d. In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
e. A student finds a correlation of r = 0.04 between the number of units the students in his research methods class are taking and the students’ level of stress.
14.2. Some Basic Null Hypothesis Tests ¶
14.2.1. learning objectives ¶.
Conduct and interpret one-sample, dependent-samples, and independent-samples t tests.
Interpret the results of one-way, repeated measures, and factorial ANOVAs.
Conduct and interpret null hypothesis tests of Pearson’s r.
In this section, we look at several common null hypothesis testing procedures. The emphasis here is on providing enough information to allow you to conduct and interpret the most basic versions. In most cases, the online statistical analysis tools mentioned in Chapter 13 will handle the computations, as will programs such as Microsoft Excel and SPSS.
14.2.2. The t Test ¶
As we have seen throughout this book, many studies in psychology focus on the difference between two means. The most common null hypothesis test for this type of statistical relationship is the t test. In this section, we look at three types of t tests that are used for slightly different research designs: the one-sample t test, the dependent-samples t test, and the independent-samples t test.
14.2.3. One-Sample t Test ¶
The one-sample t test is used to compare a sample mean (M) with a hypothetical population mean ( \(\mu_0\) ) that provides some interesting standard of comparison. The null hypothesis is that the mean for the population ( \(\mu\) ) is equal to the hypothetical population mean: \(\mu\) = \(\mu_0\) . The alternative hypothesis is that the mean for the population is different from the hypothetical population mean: \(\mu \neq \mu_0\) . To decide between these two hypotheses, we need to find the probability of obtaining the sample mean (or one more extreme) if the null hypothesis were true. But finding this p value requires first computing a test statistic called t. A test statistic is a statistic that is computed only to help find the p value. The formula for t is as follows:
Again, M is the sample mean and \(\mu_0\) is the hypothetical population mean of interest. SD is the sample standard deviation and N is the sample size.
The reason the t statistic (or any test statistic) is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 14.2: , this distribution is unimodal and symmetrical, and it has a mean of 0. Its precise shape depends on a statistical concept called the degrees of freedom, which for a one-sample t test is N - 1 (there are 24 degrees of freedom for the distribution shown in Figure 14.2: ). The important point is that knowing this distribution makes it possible to find the p value for any t score. Consider, for example, a t score of +1.50 based on a sample of 25. The probability of a t score at least this extreme is given by the proportion of t scores in the distribution that are at least this extreme. For now, let us define extreme as being far from zero in either direction. Thus the p value is the proportion of t scores that are +1.50 or above or that are -1.50 or below, a value that turns out to be .14.
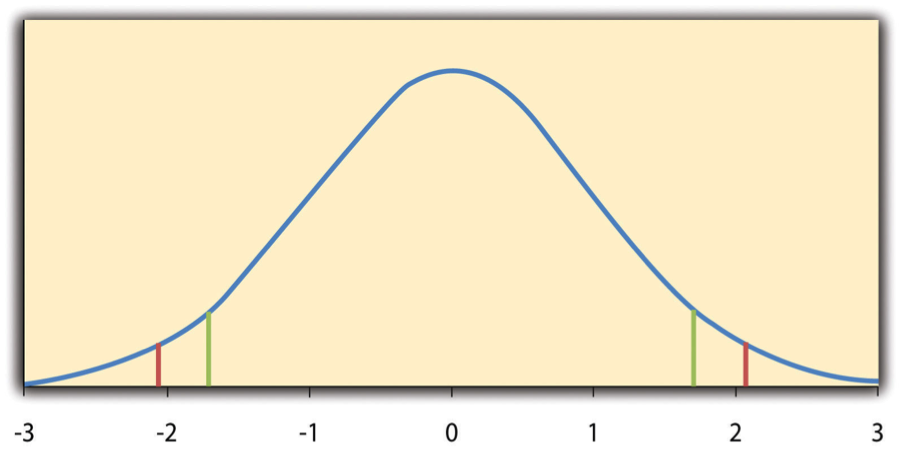
Fig. 14.2 Distribution of t Scores (with 24 Degrees of Freedom) when the null hypothesis is true. The red vertical lines represent the two-tailed critical values, and the green vertical lines the one-tailed critical values when \(\alpha\) = .05. ¶
Fortunately, we do not have to deal directly with the distribution of t scores. If we were to enter our sample data and hypothetical mean of interest into one of the online statistical tools in Chapter 13 or into a program like SPSS, the output would include both the t score and the p value. At this point, the rest of the procedure is simple. If p is less than .05, we reject the null hypothesis and conclude that the population mean differs from the hypothetical mean of interest. If p is greater than .05, we conclude that there is not enough evidence to say that the population mean differs from the hypothetical mean of interest.
If we were to compute the t score by hand, we could use a table below to make the decision. This table does not provide actual p values. Instead, it provides the critical values of t for different degrees of freedom (df) when \(\alpha\) is .05. For now, let us focus on the two-tailed critical values in the last column of the table. Each of these values should be interpreted as a pair of values: one positive and one negative. For example, the two-tailed critical values when there are 24 degrees of freedom are +2.064 and -2.064. These are represented by the red vertical lines in Figure 14.2: . The idea is that any t score below the lower critical value (the left-hand red line in Figure Figure 14.2: ) is in the lowest 2.5% of the distribution, while any t score above the upper critical value (the right-hand red line) is in the highest 2.5% of the distribution. Therefore any t score beyond the critical value in either direction is in the most extreme 5% of t scores when the null hypothesis is true and has a p value less than .05. Thus if the t score we compute is beyond the critical value in either direction, then we reject the null hypothesis. If the t score we compute is between the upper and lower critical values, then we retain the null hypothesis.
|
|
|
|---|---|---|
3 | 2.353 | 3.182 |
4 | 2.132 | 2.776 |
5 | 2.015 | 2.571 |
6 | 1.943 | 2.447 |
7 | 1.895 | 2.365 |
8 | 1.860 | 2.306 |
9 | 1.833 | 2.262 |
10 | 1.812 | 2.228 |
11 | 1.796 | 2.201 |
12 | 1.782 | 2.179 |
13 | 1.771 | 2.160 |
14 | 1.761 | 2.145 |
15 | 1.753 | 2.131 |
16 | 1.746 | 2.120 |
17 | 1.740 | 2.110 |
18 | 1.734 | 2.101 |
19 | 1.729 | 2.093 |
20 | 1.725 | 2.086 |
21 | 1.721 | 2.080 |
22 | 1.717 | 2.074 |
23 | 1.714 | 2.069 |
24 | 1.711 | 2.064 |
25 | 1.708 | 2.060 |
30 | 1.697 | 2.042 |
35 | 1.690 | 2.030 |
40 | 1.684 | 2.021 |
45 | 1.679 | 2.014 |
50 | 1.676 | 2.009 |
60 | 1.671 | 2.000 |
70 | 1.667 | 1.994 |
80 | 1.664 | 1.990 |
90 | 1.662 | 1.987 |
100 | 1.660 | 1.984 |
Thus far, we have considered what is called a two-tailed test, where we reject the null hypothesis if the t score for the sample is extreme in either direction. This test makes sense when we believe that the sample mean might differ from the hypothetical population mean but we do not have good reason to expect the difference to go in a particular direction. But it is also possible to do a one-tailed test, where we reject the null hypothesis only if the t score for the sample is extreme in one direction that we specify before collecting the data. This test makes sense when we have good reason to expect the sample mean will differ from the hypothetical population mean in a particular direction.
Here is how it works. Each one-tailed critical value in the table above can again be interpreted as a pair of values: one positive and one negative. A t score below the lower critical value is in the lowest 5% of the distribution, and a t score above the upper critical value is in the highest 5% of the distribution. For 24 degrees of freedom, these values are -1.711 and +1.711 (these are represented by the green vertical lines in Figure 14.2: ). However, for a one-tailed test, we must decide before collecting data whether we expect the sample mean to be lower than the hypothetical population mean, in which case we would use only the lower critical value, or we expect the sample mean to be greater than the hypothetical population mean, in which case we would use only the upper critical value. Notice that we still reject the null hypothesis when the t score for our sample is in the most extreme 5% of the t scores we would expect if the null hypothesis were true, keeping \(\alpha\) at .05. We have simply redefined “extreme” to refer only to one tail of the distribution. The advantage of the one-tailed test is that critical values in that tail are less extreme. If the sample mean differs from the hypothetical population mean in the expected direction, then we have a better chance of rejecting the null hypothesis. The disadvantage is that if the sample mean differs from the hypothetical population mean in the unexpected direction, then there is no chance of rejecting the null hypothesis.
14.2.4. Example One-Sample t Test ¶
Imagine that a health psychologist is interested in the accuracy of university students’ estimates of the number of calories in a chocolate chip cookie. He shows the cookie to a sample of 10 students and asks each one to estimate the number of calories in it. Because the actual number of calories in the cookie is 250, this is the hypothetical population mean of interest ( \(\mu_0\) ). The null hypothesis is that the mean estimate for the population ( \(\mu\) ) is 250. Because he has no real sense of whether the students will underestimate or overestimate the number of calories, he decides to do a two-tailed test. Now imagine further that the participants’ actual estimates are as follows:
250, 280, 200, 150, 175, 200, 200, 220, 180, 250
The mean estimate for the sample (M) is 212.00 calories and the standard deviation (SD) is 39.17. The health psychologist can now compute the t score for his sample:
If he enters the data into one of the online analysis tools or uses SPSS, it would also tell him that the two- tailed p value for this t score (with 10 - 1 = 9 degrees of freedom) is .013. Because this is less than .05, the health psychologist would reject the null hypothesis and conclude that university students tend to underestimate the number of calories in a chocolate chip cookie. If he computes the t score by hand, he could look at Table 13.2 and see that the critical value of t for a two-tailed test with 9 degrees of freedom is ±2.262. The fact that his t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
Finally, if this researcher had gone into this study with good reason to expect that university students underestimate the number of calories, then he could have done a one-tailed test instead of a two-tailed test. The only thing this decision would change is the critical value, which would be -1.833. This slightly less extreme value would make it a bit easier to reject the null hypothesis. However, if it turned out that university students overestimate the number of calories the researcher would not have been able to reject the null hypothesis, no matter how much they overestimated it.
14.2.5. The Dependent-Samples t Test ¶
The dependent-samples t test (sometimes called the paired-samples t test) is used to compare two means (e.g., a group of participants measured at two different times or under two different conditions). This comparison is appropriate for pretest-posttest designs or within-subjects experiments. The null hypothesis is that the two means are the same in the population. The alternative hypothesis is that they are not the same. Like the one-sample t test, te dependent-samples t test can be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
It helps to think of the dependent-samples t test as a special case of the one-sample t test. However, the first step in the dependent-samples t test is to reduce the two scores for each participant to a single measurement by taking the difference between them. At this point, the dependent-samples t test becomes a one-sample t test on the difference scores. The hypothetical population mean ( \(\mu_0\) ) of interest is 0 because this is what the mean difference score would be if there were no difference between the two means. We can now think of the null hypothesis as being that the mean difference score in the population is 0 ( \(\mu_0\) = 0) and the alternative hypothesis as being that the mean difference score in the population is not 0 ( \(\mu_0 \neq 0\) ).
14.2.6. Example Dependent-Samples t Test ¶
Imagine that the health psychologist now knows that people tend to underestimate the number of calories in junk food and has developed a short training program to improve their estimates. To test the effectiveness of this program, he conducts a pretest-posttest study in which 10 participants estimate the number of calories in a chocolate chip cookie before the training program and then estimate the calories again afterward. Because he expects the program to increase participants’ estimates, he decides to conduct a one-tailed test. Now imagine further that the pretest estimates are:
230, 250, 280, 175, 150, 200, 180, 210, 220, 190
and that the posttest estimates (for the same participants in the same order) are:
250, 260, 250, 200, 160, 200, 200, 180, 230, 240.
The difference scores, then, are as follows:
+20, +10, -30, +25, +10, 0, +20, -30, +10, +50.
Note that it does not matter whether the first set of scores is subtracted from the second or the second from the first as long as it is done the same way for all participants. In this example, it makes sense to subtract the pretest estimates from the posttest estimates so that positive difference scores mean that the estimates went up after the training and negative difference scores mean the estimates went down.
The mean of the difference scores is 8.50 with a standard deviation of 27.27. The health psychologist can now compute the t score for his sample as follows:
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the one-tailed p value for this t score (again with 10 - 1 = 9 degrees of freedom) is .148. Because this is greater than .05, he would fail to reject the null hypothesis; he does not have enough evidence to suggest that the training program increases calorie estimates. If he were to compute the t score by hand, he could look at the table above and see that the critical value of t for a one-tailed test with 9 degrees of freedom is +1.833 (positive because he was expecting a positive mean difference score). The fact that his t score was less extreme than this critical value would tell him that his p value is greater than .05 and that the results fail to reject the null hypothesis.
14.2.7. The Independent-Samples t Test ¶
The independent-samples t test is used to compare the means of two separate samples (M1 and M2). The two samples might have been tested under different conditions in a between-subjects experiment, or they could be preexisting groups in a correlational design (e.g., women and men or extraverts and introverts). The null hypothesis is that the two means: \(\mu_1 = \) \mu_2 \(. The alternative hypothesis is that they are not the same: \) \mu_1 \neq \mu_2$. Again, the test can be one-tailed if the researcher has good reason to expect the difference goes in a particular direction.
The t statistic here is a bit more complicated because it must take into account two sample means, two standard deviations, and two sample sizes. The formula is as follows:
Notice that this formula includes squared standard deviations (the variances) that appear inside the square root symbol. Also, lowercase n1 and n2 refer to the sample sizes in the two groups or condition (as opposed to capital N, which generally refers to the total sample size). The only additional thing to know here is that there are N - 2 degrees of freedom for the independent-samples t test.
14.2.8. Example Independent-Samples t test ¶
Now the health psychologist wants to compare the calorie estimates of people who regularly eat junk food with the estimates of people who rarely eat junk food. He believes the difference could come out in either direction so he decides to conduct a two-tailed test. He collects data from a sample of eight participants who eat junk food regularly and seven participants who rarely eat junk food. The data are as follows:
Junk food eaters: 180, 220, 150, 85, 200, 170, 150, 190
Non–junk food eaters: 200, 240, 190, 175, 200, 300, 240
The mean for the junk food eaters is 220.71 with a standard deviation of 41.23. The mean for the non–junk food eaters is 168.12 with a standard deviation of 42.66. He can now compute his t score as follows:
If he enters the data into one of the online analysis tools or uses Excel or SPSS, it would tell him that the two-tailed p value for this t score (with 15 - 2 = 13 degrees of freedom) is .015. Because this p value is less than .05, the health psychologist would reject the null hypothesis and conclude that people who eat junk food regularly make lower calorie estimates than people who eat it rarely. If he were to compute the t score by hand, he could look at the table above and see that the critical value of t for a two-tailed test with 13 degrees of freedom is 2.160 (and/or -2.160). The fact that the observed t score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
14.2.9. The Analysis of Variance ¶
When there are more than two groups or condition means to be compared, the most common null hypothesis test is the analysis of variance (ANOVA). In this section, we look primarily at the one-way ANOVA, which is used for between-subjects designs with a single independent variable. We then briefly consider some other versions of the ANOVA that are used for within-subjects and factorial research designs.
14.2.10. One-Way ANOVA ¶
The one-way ANOVA is used to compare the means of more than two samples ( \(M_1, M_2, \ldots M_G\) ) in a between-subjects design. The null hypothesis is that all the means are equal in the population: \(\mu_1=\mu_2= \ldots = \mu_G\) . The alternative hypothesis is that not all the means in the population are equal.
The test statistic for the ANOVA is called F. It is a ratio of two estimates of the population variance based on the sample data. One estimate of the population variance is called the mean squares between groups (MSB) and is based on the differences among the sample means. The other is called the mean squares within groups (MSW) and is based on the differences among the scores within each group. The F statistic is the ratio of the \(MS_B\) to the \(MS_W\) and can therefore be expressed as follows:
Again, the reason that F is useful is that we know how it is distributed when the null hypothesis is true. As shown in Figure 14.3: , this distribution is unimodal and positively skewed with values that cluster around 1. The precise shape of the distribution depends on both the number of groups and the sample size, and there is a degrees of freedom value associated with each of these. The between-groups degrees of freedom is the number of groups minus one: \(df_B = (G - 1)\) . The within-groups degrees of freedom is the total sample size minus the number of groups: \(df_W = N - G\) . Again, knowing the distribution of F when the null hypothesis is true allows us to find the p value.
As with the t test, there are online tools and statistical software such as Excel and SPSS that will compute F and find the p value for you. If p is less than .05, then we reject the null hypothesis and conclude that there are differences among the group means in the population.
Fig. 14.3 Distribution of the F Ratio With 2 and 37 Degrees of Freedom When the Null Hypothesis Is True. The red vertical line represents the critical value when \(\alpha\) is .05. ¶
If p is greater than .05, then we cannot reject the null hypothesis and conclude that there is not enough evidence to say that there are differences. In the unlikely event that we would compute F by hand, we can use a table of critical values like those in the table below to make the decision. The idea is that any F ratio greater than the critical value has a p value of less than .05. Thus if the F ratio we compute is beyond the critical value, then we reject the null hypothesis. If the F ratio we compute is less than the critical value, then we retain the null hypothesis.
\(df_W\) | \(df_B=2\) | \(df_B=3\) | \(df_B=4\) |
|---|---|---|---|
8 | 4.459 | 4.066 | 3.838 |
9 | 4.256 | 3.863 | 3.633 |
10 | 4.103 | 3.708 | 3.478 |
11 | 3.982 | 3.587 | 3.357 |
12 | 3.885 | 3.490 | 3.259 |
13 | 3.806 | 3.411 | 3.179 |
14 | 3.739 | 3.344 | 3.112 |
15 | 3.682 | 3.287 | 3.056 |
16 | 3.634 | 3.239 | 3.007 |
17 | 3.592 | 3.197 | 2.965 |
18 | 3.555 | 3.160 | 2.928 |
19 | 3.522 | 3.127 | 2.895 |
20 | 3.493 | 3.098 | 2.866 |
21 | 3.467 | 3.072 | 2.840 |
22 | 3.443 | 3.049 | 2.817 |
23 | 3.422 | 3.028 | 2.796 |
24 | 3.403 | 3.009 | 2.776 |
25 | 3.385 | 2.991 | 2.759 |
30 | 3.316 | 2.922 | 2.690 |
35 | 3.267 | 2.874 | 2.641 |
40 | 3.232 | 2.839 | 2.606 |
45 | 3.204 | 2.812 | 2.579 |
50 | 3.183 | 2.790 | 2.557 |
55 | 3.165 | 2.773 | 2.540 |
60 | 3.150 | 2.758 | 2.525 |
65 | 3.138 | 2.746 | 2.513 |
70 | 3.128 | 2.736 | 2.503 |
75 | 3.119 | 2.727 | 2.494 |
80 | 3.111 | 2.719 | 2.486 |
85 | 3.104 | 2.712 | 2.479 |
90 | 3.098 | 2.706 | 2.473 |
95 | 3.092 | 2.700 | 2.467 |
100 | 3.087 | 2.696 | 2.463 |
14.2.11. Example One-Way ANOVA ¶
Imagine that the health psychologist wants to compare the calorie estimates of psychology majors, nutrition majors, and professional dieticians. He collects the following data:
Psych majors: 200, 180, 220, 160, 150, 200, 190, 200
Nutrition majors: 190, 220, 200, 230, 160, 150, 200, 210, 195
Dieticians: 220, 250, 240, 275, 250, 230, 200, 240
The means are 187.50 (SD = 23.14), 195.00 (SD = 27.77), and 238.13 (SD = 22.35), respectively. So it appears that dieticians made substantially more accurate estimates on average. The researcher would almost certainly enter these data into a program such as Excel or SPSS, which would compute F for him and find the p value. The table below shows the output you might see when performing a one-way ANOVA on these results. This table is referred to as an ANOVA table. It shows that \(MS_B\) is 5,971.88, \(MS_W\) is 602.23, and their ratio, F, is 9.92. The p value is .0009. Because this value is below .05, the researcher would reject the null hypothesis and conclude that the mean calorie estimates for the three groups are not the same in the population. Notice that the ANOVA table also includes the “sum of squares” (SS) for between groups and for within groups. These values are computed on the way to finding \(MS_B\) and \(MS_W\) but are not typically reported by the researcher. Finally, if the researcher were to compute the F ratio by hand, he could look at the table above and see that the critical value of F with 2 and 21 degrees of freedom is 3.467. The fact that his F score was more extreme than this critical value would tell him that his p value is less than .05 and that he should reject the null hypothesis.
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
Between groups | 11,943.75 | 2 | 5,971.875 | 9.916234 | 0.000928 | 3.4668 |
Within groups | 12,646.88 | 21 | 602.2321 | |||
Total | 24,590.63 | 23 |
14.2.12. ANOVA Elaborations ¶
14.2.12.1. post hoc comparisons ¶.
When we reject the null hypothesis in a one-way ANOVA, we conclude that the group means are not all the same in the population. But this can indicate different things. With three groups, it can indicate that all three means are significantly different from each other. Or it can indicate that one of the means is significantly different from the other two, but the other two are not significantly different from each other. It could be, for example, that the mean calorie estimates of psychology majors, nutrition majors, and dieticians are all significantly different from each other. Or it could be that the mean for dieticians is significantly different from the means for psychology and nutrition majors, but the means for psychology and nutrition majors are not significantly different from each other. For this reason, statistically significant one-way ANOVA results are typically followed up with a series of post hoc comparisons of selected pairs of group means to determine which are different from which others.
One approach to post hoc comparisons would be to conduct a series of independent-samples t tests comparing each group mean to each of the other group means. But there is a problem with this approach. In general, if we conduct a t test when the null hypothesis is true, we have a 5% chance of mistakenly rejecting the null hypothesis. If we conduct several t tests when the null hypothesis is true, the chance of mistakenly rejecting at least one null hypothesis increases with each test we conduct. Thus, researchers do not usually make post hoc comparisons using standard t tests because there is too great a chance that they will mistakenly reject at least one null hypothesis. Instead, they use one of several modified t test procedures, including the Bonferonni procedure, Fisher’s least significant difference (LSD) test, and Tukey’s honestly significant difference (HSD) test. The details of these approaches are beyond the scope of this book, but it is important to understand their purpose. It is to keep the risk of mistakenly rejecting a true null hypothesis to an acceptable level (close to 5%).
14.2.12.2. Repeated-Measures ANOVA ¶
Recall that the one-way ANOVA is appropriate for between-subjects designs in which the means being compared come from separate groups of participants. It is not appropriate for within-subjects designs in which the means being compared come from the same participants tested under different conditions or at different times. This requires a slightly different approach, called the repeated-measures ANOVA. The basics of the repeated-measures ANOVA are the same as for the one-way ANOVA. The main difference is that measuring the dependent variable multiple times for each participant allows for a more refined measure of \(MS_W\) . Imagine, for example, that the dependent variable in a study is a measure of reaction time. Some participants will be faster or slower than others overall. This may be because of stable individual differences in their nervous systems, muscles, and other factors. In a between-subjects design, these stable individual differences would simply add to the variability within the groups and increase the value of \(MS_W\) . In a within-subjects design, however, these stable individual differences can be measured and subtracted from the value of \(MS_W\) . This lower value of \(MS_W\) means a higher value of F and a more sensitive test.
14.2.12.3. Factorial ANOVA ¶
When more than one independent variable is included in a factorial design, the appropriate approach is the factorial ANOVA. Again, the basics of the factorial ANOVA are the same as for the one-way and repeated- measures ANOVAs. The main difference is that it produces an F ratio and p value for each main effect and for each interaction. Returning to our calorie estimation example, imagine that the health psychologist tests the effect of participant major (psychology vs. nutrition) and food type (cookie vs. hamburger) in a factorial design. A factorial ANOVA would produce separate F ratios and p values for the main effect of major, the main effect of food type, and the interaction between major and food. Appropriate modifications must be made depending on whether the design is between subjects, within subjects, or mixed.
14.2.13. Testing Pearson’s r ¶
For relationships between quantitative variables, where Pearson’s r is used to describe the strength of those relationships, the appropriate null hypothesis test is a test of Pearson’s r. The basic logic is exactly the same as for other null hypothesis tests. In this case, the null hypothesis is that there is no relationship in the population. We can use the Greek lowercase rho ( \(\rho\) ) to represent the relevant parameter: \(\rho = 0\) . The alternative hypothesis is that there is a relationship in the population: \(\rho \neq 0\) . As with the t test, this test can be two-tailed if the researcher has no expectation about the direction of the relationship or one-tailed if the researcher expects the relationship to go in a particular direction.
It is possible to use Pearson’s r for the sample to compute a t score with N - 2 degrees of freedom and then to proceed as for a t test. However, because of the way it is computed, Pearson’s r can also be treated as its own test statistic. The online statistical tools and statistical software such as Excel and SPSS generally compute Pearson’s r and provide the p value associated with that value of Pearson’s r. As always, if the p value is less than .05, we reject the null hypothesis and conclude that there is a relationship between the variables in the population. If the p value is greater than .05, we retain the null hypothesis and conclude that there is not enough evidence to say there is a relationship in the population. If we compute Pearson’s r by hand, we can use a table like the one below, which shows the critical values of r for various samples sizes when \(\alpha\) is .05. A sample value of Pearson’s r that is more extreme than the critical value is statistically significant.
|
|
|
|---|---|---|
5 | .805 | .878 |
10 | .549 | .632 |
15 | .441 | .514 |
20 | .378 | .444 |
25 | .337 | .396 |
30 | .306 | .361 |
35 | .283 | .334 |
40 | .264 | .312 |
45 | .248 | .294 |
50 | .235 | .279 |
55 | .224 | .266 |
60 | .214 | .254 |
65 | .206 | .244 |
70 | .198 | .235 |
75 | .191 | .227 |
80 | .185 | .220 |
85 | .180 | .213 |
90 | .174 | .207 |
95 | .170 | .202 |
100 | .165 | .197 |
14.2.14. Example Test of Pearson’s r ¶
Imagine that the health psychologist is interested in the correlation between people’s calorie estimates and their weight. He has no expectation about the direction of the relationship, so he decides to conduct a two-tailed test. He computes the correlation for a sample of 22 university students and finds that Pearson’s r is -0.21. The statistical software he uses tells him that the p value is 0.348. It is greater than .05, so he cannot reject the null hypothesis and concludes that there is not enough evidence to suggest a relationship between people’s calorie estimates and their weight. If he were to compute Pearson’s r by hand, he could look at the table above and see that the critical value for 22 - 2 = 20 degrees of freedom is .444. The fact that Pearson’s r for the sample is less extreme than this critical value tells him that the p value is greater than .05 and that he should retain the null hypothesis.
14.2.15. Key Takeaways ¶
To compare two means, the most common null hypothesis test is the t test. The one-sample t test is used for comparing one sample mean with a hypothetical population mean of interest, the dependent-samples t test is used to compare two means in a within-subjects design, and the independent-samples t test is used to compare two means in a between-subjects design.
To compare more than two means, the most common null hypothesis test is the analysis of variance (ANOVA). The one-way ANOVA is used for between-subjects designs with one independent variable, the repeated-measures ANOVA is used for within-subjects designs, and the factorial ANOVA is used for factorial designs.
A null hypothesis test of Pearson’s r is used to compare a sample value of Pearson’s r with a hypothetical population value of 0.
14.2.16. Exercises ¶
Practice: Use one of the online tools, Excel, or SPSS to reproduce the one-sample t test, dependent-samples t test, independent-samples t test, and one-way ANOVA for the four sets of calorie estimation data presented in this section.
Practice: A sample of 25 university students rated their friendliness on a scale of 1 (Much Lower Than Average) to 7 (Much Higher Than Average). Their mean rating was 5.30 with a standard deviation of 1.50. Conduct a one-sample t test comparing their mean rating with a hypothetical mean rating of 4 (Average). The question is whether university students have a tendency to rate themselves as friendlier than average.
Practice: Decide whether each of the following Pearson’s r values is statistically significant for both a one-tailed and a two-tailed test.
a. The correlation between height and IQ is +.13 in a sample of 35.
b. For a sample of 88 university students, the correlation between how disgusted they felt and the harshness of their moral judgments was +.23.
c. The correlation between the number of daily hassles and positive mood is -.43 for a sample of 30 middle-aged adults.
14.3. Additional Considerations ¶
14.3.1. learning objectives ¶.
Define Type I and Type II errors, explain why they occur, and identify some steps that can be taken to minimize their likelihood.
Define statistical power, explain its role in the planning of new studies, and use online tools to compute the statistical power of simple research designs.
List some criticisms of conventional null hypothesis testing, along with some ways of dealing with these criticisms.
In this section, we consider a few other issues related to null hypothesis testing, including some that are useful in planning studies and interpreting results. We even consider some long-standing criticisms of null hypothesis testing, along with some steps that researchers in psychology have taken to address them.
14.3.2. Errors in Null Hypothesis Testing ¶
In null hypothesis testing, the researcher tries to draw a reasonable conclusion about the population based on the sample. Unfortunately, this conclusion is not guaranteed to be correct. This discrepancy is illustrated by Figure 14.4: . The rows of this table represent the two possible decisions that we can make: to reject or retain the null hypothesis. The columns represent the two possible states of the world: the null hypothesis is false or it is true. The four cells of the table, then, represent the four distinct outcomes of a null hypothesis test. Two of the outcomes are correct: rejecting the null hypothesis when it is false and retaining it when it is true. The other two are errors: rejecting the null hypothesis when it is true and retaining it when it is false.
Rejecting the null hypothesis when it is true is called a Type I error. This error means that we have concluded that there is a relationship in the population when in fact there is not. Type I errors occur because even when there is no relationship in the population, sampling error alone will occasionally produce an extreme result. In fact, when the null hypothesis is true and \(\alpha\) is .05, we will mistakenly reject the null hypothesis 5% of the time (thus \(\alpha\) is sometimes referred to as the “Type I error rate”). Retaining the null hypothesis when it is false is called a Type II error. This error means that we have concluded that there is no relationship in the population when in fact there is. In practice, Type II errors occur primarily because the research design lacks adequate statistical power to detect the relationship (e.g., the sample is too small). We will have more to say about statistical power shortly.
In principle, it is possible to reduce the chance of a Type I error by setting \(\alpha\) to something less than .05. Setting it to .01, for example, would mean that if the null hypothesis is true, then there is only a 1% chance of mistakenly rejecting it. But making it harder to reject true null hypotheses also makes it harder to reject false ones and therefore increases the chance of a Type II error. Similarly, it is possible to reduce the chance of a Type II error by setting \(\alpha\) to something greater than .05 (e.g., .10). But making it easier to reject false null hypotheses also makes it easier to reject true ones and therefore increases the chance of a Type I error. This provides some insight into why the convention is to set \(\alpha\) to .05. The conventional level of \(\alpha=.05\) represents a particular balance between the rates of both Type I and Type II errors.
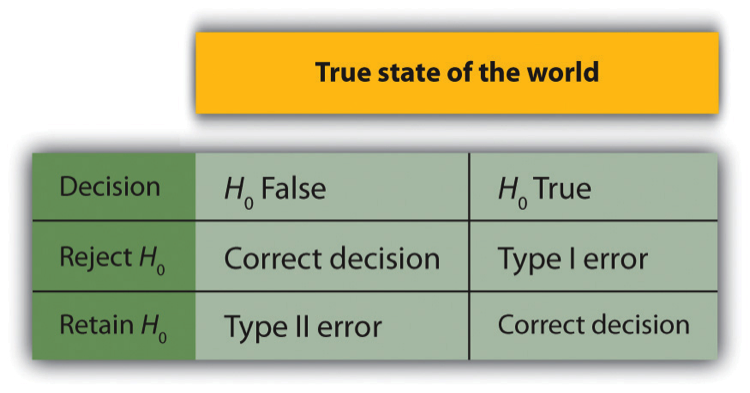
Fig. 14.4 Two Types of Correct Decisions and Two Types of Errors in Null Hypothesis Testing ¶
The possibility of committing Type I and Type II errors has several important implications for interpreting the results of our own and others’ research. One is that we should be cautious about interpreting the results of any individual study because there is a chance that it’s results reflect a Type I or Type II error. This possibility is why researchers consider it important to replicate their studies. Each time researchers replicate a study and find a similar result, they rightly become more confident that the result represents a real phenomenon and not just a Type I or Type II error.
Another issue related to Type I errors is the so-called file drawer problem [Ros79] . The idea is that when researchers obtain statistically significant results, they tend to submit them for publication, and journal editors and reviewers tend to accept them. But when researchers obtain non-significant results, they tend not to submit them for publication, or if they do submit them, journal editors and reviewers tend not to accept them. Researchers end up putting these non-significant results away in a file drawer (or nowadays, in a folder on their hard drive). One effect of this tendency is that the published literature probably contains a higher proportion of Type I errors than we might expect on the basis of statistical considerations alone. Even when there is a relationship between two variables in the population, the published research literature is likely to overstate the strength of that relationship. Imagine, for example, that the relationship between two variables in the population is positive but weak (e.g., \(\rho\) = +0.10). If several researchers conduct studies on this relationship, sampling error is likely to produce results ranging from weak negative relationships (e.g., r = -0.10) to moderately strong positive ones (e.g., r = +0.40). But because of the file drawer problem, it is likely that only those studies producing moderate to strong positive relationships are published. The result is that the effect reported in the published literature tends to be stronger than it really is in the population.
The file drawer problem is a difficult one because it is a product of the way scientific research has traditionally been conducted and published. One solution might be for journal editors and reviewers to evaluate research submitted for publication without knowing the results of that research. The idea is that if the research question is judged to be interesting and the method judged to be sound, then a non-significant result should be just as important and worthy of publication as a significant one. Short of such a radical change in how research is evaluated for publication, researchers can still take pains to keep their non-significant results and share them as widely as possible (e.g., at professional conferences). Many scientific disciplines now have mechanisms for publishing non-significant results. In psychology, for example, there is an increasing use of registered reprorts, which are studies that are designed and reviewed before ever being conducted. Because publishing decisions are made before data is collected and before making statistical decisions, the literature is less likely to be biased by the file drawer problem.
In 2014, Uri Simonsohn, Leif Nelson, and Joseph Simmons published a leveling article at the field of psychology accusing researchers of creating too many Type I errors in psychology by chasing a significant p value through what they called p-hacking [SNS14] . Researchers are trained in many sophisticated statistical techniques for analyzing data that will yield a desirable p value. They propose using a p-curve to determine whether the data set with a certain p value is credible or not. They also propose this p-curve as a way to unlock the file drawer because we can only understand the finding if we know the true effect size and the likelihood of a result was found after multiple attempts at not finding a result. Their groundbreaking paper contributed to a major conversation in the field about publishing standards and the reliability of our results.
14.3.3. Statistical Power ¶
The statistical power of a research design is the probability of rejecting the null hypothesis given the sample size and expected relationship strength. For example, the statistical power of a study with 50 participants and an expected Pearson’s r of 0.30 in the population is 0.59. That is, there is a 59% chance of rejecting the null hypothesis if indeed the population correlation is 0.30. Statistical power is the complement of the probability of committing a Type II error. So in this example, the probability of committing a Type II error would be 1 - .59 = .41. Clearly, researchers should be interested in the power of their research designs if they want to avoid making Type II errors. In particular, they should make sure their research design has adequate power before collecting data. A common guideline is that a power of .80 is adequate. This guideline means that there is an 80% chance of rejecting the null hypothesis for the expected relationship strength.
The topic of how to compute power for various research designs and null hypothesis tests is beyond the scope of this book. However, there are online tools that allow you to do this by entering your sample size, expected relationship strength, and \(\alpha\) level for various hypothesis tests (see below). In addition, Figure 14.5 shows the sample size needed to achieve a power of .80 for weak, medium, and strong relationships for a two- tailed independent-samples t test and for a two-tailed test of Pearson’s r. Notice that this table amplifies the point made earlier about relationship strength, sample size, and statistical significance. In particular, weak relationships require very large samples to provide adequate statistical power.
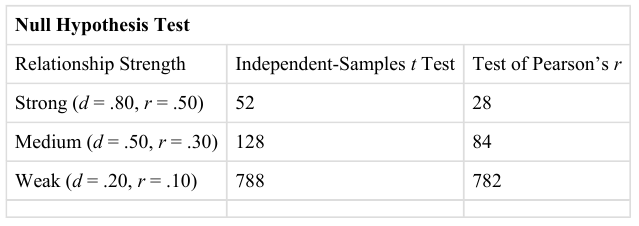
Fig. 14.5 Sample sizes needed to achieve statistical power of .80 for different expected relationship strengths for an independent-samples t test and a test of pearson’s r null hypothesis test ¶
What should you do if you discover that your research design does not have adequate power? Imagine, for example, that you are conducting a between-subjects experiment with 20 participants in each of two conditions and that you expect a medium difference (d = .50) in the population. The statistical power of this design is only .34. That is, even if there is a medium difference in the population, there is only about a one in three chance of rejecting the null hypothesis and about a two in three chance of committing a Type II error.
Given the time and effort involved in conducting the study, this probably seems like an unacceptably low chance of rejecting the null hypothesis and an unacceptably high chance of committing a Type II error. Given that statistical power depends primarily on relationship strength and sample size, there are essentially two steps you can take to increase statistical power: increase the strength of the relationship or increase the sample size. Increasing the strength of the relationship can sometimes be accomplished by using a stronger manipulation or by more carefully controlling extraneous variables to reduce the amount of noise in the data (e.g., by using a within-subjects design rather than a between-subjects design). The usual strategy, however, is to increase the sample size. For any expected relationship strength, there will always be some sample large enough to achieve adequate power.
14.3.4. Computing Power Online ¶
The following links are to tools that allow you to compute statistical power for various research designs and null hypothesis tests by entering information about the expected relationship strength, the sample size, and the \(\alpha\) level. They also allow you to compute the sample size necessary to achieve your desired level of power (e.g., .80). The first is an online tool. The second is a free downloadable program called G*Power.
Russ Lenth’s Power and Sample Size Page
14.3.5. Problems With Null Hypothesis Testing, and Some Solutions ¶
Again, null hypothesis testing is the most common approach to inferential statistics in psychology. It is not without its critics, however. In fact, in recent years the criticisms have become so prominent that the American Psychological Association convened a task force to make recommendations about how to deal with them [Wil99] . In this section, we consider some of the criticisms and some of the recommendations.
14.3.6. Criticisms of Null Hypothesis Testing ¶
Some criticisms of null hypothesis testing focus on researchers’ misunderstanding of it. We have already seen, for example, that the p value is widely misinterpreted as the probability that the null hypothesis is true (recall that it is really the probability of the sample result if the null hypothesis were true). A closely related misinterpretation is that 1 - p is the probability of replicating a statistically significant result. In one study, 60% of a sample of professional researchers thought that a p value of .01 (for an independent-samples t test with 20 participants in each sample) meant there was a 99% chance of replicating the statistically significant result [Oak86] . Our earlier discussion of power should make it clear that this figure is far too optimistic. As the table of critical values of Pearson’s r presented above, even if there were a large difference between means in the population, it would require 26 participants per sample to achieve a power of .80. And the program G*Power shows that it would require 59 participants per sample to achieve a power of .99.
Another set of criticisms focuses on the logic of null hypothesis testing. To many, the strict convention of rejecting the null hypothesis when p is less than .05 and retaining it when p is greater than .05 makes little sense. This criticism does not have to do with the specific value of .05 but with the idea that there should be any rigid dividing line between results that are considered significant and results that are not. Imagine two studies on the same statistical relationship with similar sample sizes. One has a p value of .04 and the other a p value of .06. Although the two studies have produced essentially the same result, the former is likely to be considered interesting and worthy of publication and the latter simply not significant. This convention is likely to prevent good research from being published and to contribute to the file drawer problem.
Yet another set of criticisms focus on the idea that null hypothesis testing, even when understood and carried out correctly, is simply not very informative. Recall that the null hypothesis is that there is no relationship between variables in the population (e.g., Cohen’s d or Pearson’s r is precisely 0). So to reject the null hypothesis is simply to say that there is some nonzero relationship in the population. But this assertion is not really saying very much. Imagine if chemistry could tell us only that there is some relationship between the temperature of a gas and its volume, rather than providing a precise equation to describe that relationship. Some critics even argue that the relationship between two variables in the population is never precisely 0 if it is carried out to enough decimal places. In other words, the null hypothesis is never literally true. So rejecting it does not tell us anything we did not already know!
To be fair, many researchers have come to the defense of null hypothesis testing. One of them, Robert Abelson, has argued that when it is correctly understood and carried out, null hypothesis testing does serve an important purpose [Abe12] . Especially when dealing with new phenomena, it gives researchers a principled way to convince others that their results should not be dismissed as mere chance occurrences.
14.3.7. The end of p-values? ¶
In 2015, the editors of Basic and Applied Social Psychology announced6 a ban on the use of null hypothesis testing and related statistical procedures. Authors are welcome to submit papers with p-values, but the editors will remove them before publication. Although they did not propose a better statistical test to replace null hypothesis testing, the editors emphasized the importance of descriptive statistics and effect sizes. This rejection of the “gold standard” of statistical validity has continued the conversation in psychology of questioning exactly what we know.
14.3.8. What to Do? ¶
Even those who defend null hypothesis testing recognize many of the problems with it. But what should be done? Some suggestions now appear in the Publication Manual. One is that each null hypothesis test should be accompanied by an effect size measure such as Cohen’s d or Pearson’s r. By doing so, the researcher provides an estimate of how strong the relationship in the population is—not just whether there is one or not. Remember that the p value cannot be interpreted as a direct measure of relationship strength because it also depends on the sample size. Even a very weak result can be statistically significant if the sample is large enough.
Another suggestion is to use confidence intervals rather than null hypothesis tests. A confidence interval around a statistic is a range of values that are likely to include the population parameter. For example, a sample of 20 university students might have a mean calorie estimate for a chocolate chip cookie of 200 with a 95% confidence interval of 160 to 240. Advocates of confidence intervals argue that they are much easier to interpret than null hypothesis tests. Another advantage of confidence intervals is that they provide the information necessary to do null hypothesis tests should anyone want to. In this example, the sample mean of 200 is significantly different at the .05 level from any hypothetical population mean that lies outside the confidence interval. So the confidence interval of 160 to 240 tells us that the sample mean is statistically significantly different from a hypothetical population mean of 250.
Finally, there are more radical solutions to the problems of null hypothesis testing that involve using very different approaches to inferential statistics. Bayesian statistics, for example, is an approach in which the researcher specifies the probability that the null hypothesis and any important alternative hypotheses are true before conducting the study, conducts the study, and then updates the probabilities based on the data. It is too early to say whether this approach will become common in psychological research. For now, null hypothesis testing, complemented by effect size measures and confidence intervals, remains the dominant approach.
14.3.9. Key Takeaways ¶
The decision to reject or retain the null hypothesis is not guaranteed to be correct. A Type I error occurs when one rejects the null hypothesis when it is true. A Type II error occurs when one fails to reject the null hypothesis when it is false.
The statistical power of a research design is the probability of rejecting the null hypothesis given the expected relationship strength in the population and the sample size. Researchers should make sure that their studies have adequate statistical power before conducting them.
Null hypothesis testing has been criticized on the grounds that researchers misunderstand it, that it is illogical, and that it is uninformative. Others argue that it serves an important purpose—especially when used with effect size measures, confidence intervals, and other techniques. It remains the dominant approach to inferential statistics in psychology.
14.3.10. Exercises ¶
Discussion: A researcher compares the effectiveness of two forms of psychotherapy for social phobia using an independent-samples t test. a. Explain what it would mean for the researcher to commit a Type I error. b. Explain what it would mean for the researcher to commit a Type II error.
Discussion: Imagine that you conduct a t test and the p value is .02. How could you explain what this p value means to someone who is not already familiar with null hypothesis testing? Be sure to avoid the common misinterpretations of the p value.
For additional practice with Type I and Type II errors, try these problems from Carnegie Mellon’s Open Learning Initiative.

14.4. From the “Replication Crisis” to Open Science Practices ¶
14.4.1. learning objectives ¶.
Describe what is meant by the “replication crisis” in psychology.
Describe some questionable research practices.
Identify some ways in which scientific rigor may be increased.
Understand the importance of openness in psychological science.
At the start of this book we discussed the “Many Labs Replication Project”, which failed to replicate the original finding by Simone Schnall and her colleagues that washing one’s hands leads people to view moral transgressions as less wrong [SBH08] . Although this project is a good illustration of the collaborative and self-correcting nature of science, it also represents one specific response to psychology’s recent replication crisis”, a phrase that refers to the inability of researchers to replicate earlier research findings. Consider for example the results of the Reproducibility Project, which involved over 270 psychologists around the world coordinating their efforts to test the reliability of 100 previously published psychological experiments [C+15] . Although 97 of the original 100 studies had found statistically significant effects, only 36 of the replications did! Moreover, even the effect sizes of the replications were, on average, half of those found in the original studies (see Figure 13.5). Of course, a failure to replicate a result by itself does not necessarily discredit the original study as differences in the statistical power, populations sampled, and procedures used, or even the effects of moderating variables could explain the different results.
Although many believe that the failure to replicate research results is an expected characteristic of cumulative scientific progress, others have interpreted this situation as evidence of systematic problems with conventional scholarship in psychology, including a publication bias that favors the discovery and publication of counter-intuitive but statistically significant findings instead of the duller (but incredibly vital) process of replicating previous findings to test their robustness [PH12] .
Worse still is the suggestion that the low replicability of many studies is evidence of the widespread use of questionable research practices by psychological researchers. These may include:
The selective deletion of outliers in order to influence (usually by artificially inflating) statistical relationships among the measured variables.
The selective reporting of results, cherry-picking only those findings that support one’s hypotheses.
Mining the data without an a priori hypothesis, only to claim that a statistically significant result had been originally predicted, a practice referred to as “HARKing” or hypothesizing after the results are known [Ker98] .
A practice colloquially known as “p-hacking” (briefly discussed in the previous section), in which a researcher might perform inferential statistical calculations to see if a result was significant before deciding whether to recruit additional participants and collect more data [HHL+15] . As you have learned, the probability of finding a statistically significant result is influenced by the number of participants in the study.
Outright fabrication of data (as in the case of Diederik Stapel, described at the start of Chapter 3), although this would be a case of fraud rather than a “research practice”.
It is important to shed light on these questionable research practices to ensure that current and future researchers (such as yourself) understand the damage they wreak to the integrity and reputation of our discipline (see, for example, the “Replication Index”, a statistical “doping test” developed by Ulrich Schimmack in 2014 for estimating the replicability of studies, journals, and even specific researchers). However, in addition to highlighting what not to do, this so-called “crisis” has also highlighted the importance of enhancing scientific rigor by:
Designing and conducting studies that have sufficient statistical power, in order to increase the reliability of findings.
Publishing both null and significant findings (thereby counteracting the publication bias and reducing the file drawer problem).
Describing one’s research designs in sufficient detail to enable other researchers to replicate your study using an identical or at least very similar procedure.
Conducting high-quality replications and publishing these results [BID+14] .
One particularly promising response to the replicability crisis has been the emergence of open science practices that increase the transparency and openness of the scientific enterprise. For example, Psychological Science (the flagship journal of the Association for Psychological Science) and other journals now issue digital badges to researchers who pre-registered their hypotheses and data analysis plans, openly shared their research materials with other researchers (e.g., to enable attempts at replication), or made available their raw data with other researchers (see Figure 13.6).
These initiatives, which have been spearheaded by the Center for Open Science, have led to the development of Transparency and Openness Promotion guidelines that have since been formally adopted by more than 500 journals and 50 organizations, a list that grows each week. When you add to this the requirements recently imposed by federal funding agencies in Canada (the Tri-Council) and the United States (National Science Foundation) concerning the publication of publicly-funded research in open access journals, it certainly appears that the future of science and psychology will be one that embraces greater “openness” [NAB+15] .
14.4.2. Key Takeaways ¶
In recent years psychology has grappled with a failure to replicate research findings. Some have interpreted this as a normal aspect of science but others have suggested that this is highlights problems stemming from questionable research practices.
One response to this “replicability crisis” has been the emergence of open science practices, which increase the transparency and openness of the research process. These open practices include digital badges to encourage pre-registration of hypotheses and the sharing of raw data and research materials.
14.4.3. Exercises ¶
Discussion: What do you think are some of the key benefits of the adoption of open science practices such as pre-registration and the sharing of raw data and research materials? Can you identify any drawbacks of these practices?
Practice: Read the online article “Science isn’t broken: It’s just a hell of a lot harder than we give it credit for” and use the interactive tool entitled “Hack your way to scientific glory” in order to better understand the data malpractice of “p-hacking.”

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Inferential Statistics
Recall that Matthias Mehl and his colleagues, in their study of sex differences in talkativeness, found that the women in their sample spoke a mean of 16,215 words per day and the men a mean of 15,669 words per day (Mehl, Vazire, Ramirez-Esparza, Slatcher, & Pennebaker, 2007) [1] . But despite this sex difference in their sample, they concluded that there was no evidence of a sex difference in talkativeness in the population. Recall also that Allen Kanner and his colleagues, in their study of the relationship between daily hassles and symptoms, found a correlation of +.60 in their sample (Kanner, Coyne, Schaefer, & Lazarus, 1981) [2] . But they concluded that this finding means there is a relationship between hassles and symptoms in the population. This assertion raises the question of how researchers can say whether their sample result reflects something that is true of the population.
The answer to this question is that they use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research. We begin with a conceptual overview of null hypothesis testing, including its purpose and basic logic. Then we look at several null hypothesis testing techniques for drawing conclusions about differences between means and about correlations between quantitative variables. Finally, we consider a few other important ideas related to null hypothesis testing, including some that can be helpful in planning new studies and interpreting results. We also look at some long-standing criticisms of null hypothesis testing and some ways of dealing with these criticisms.
- Mehl, M. R., Vazire, S., Ramirez-Esparza, N., Slatcher, R. B., & Pennebaker, J. W. (2007). Are women really more talkative than men? Science, 317 , 82. ↵
- Kanner, A. D., Coyne, J. C., Schaefer, C., & Lazarus, R. S. (1981). Comparison of two modes of stress measurement: Daily hassles and uplifts versus major life events. Journal of Behavioral Medicine, 4 , 1–39. ↵
Research Methods in Psychology Copyright © 2019 by Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Popular searches
- How to Get Participants For Your Study
- How to Do Segmentation?
- Conjoint Preference Share Simulator
- MaxDiff Analysis
- Likert Scales
- Reliability & Validity
Request consultation
Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.
Looking for an online survey platform?
Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.
Research Methods Knowledge Base
- Navigating the Knowledge Base
- Foundations
- Measurement
- Research Design
- Conclusion Validity
- Data Preparation
- Descriptive Statistics
- Dummy Variables
- General Linear Model
- Posttest-Only Analysis
- Factorial Design Analysis
- Randomized Block Analysis
- Analysis of Covariance
- Nonequivalent Groups Analysis
- Regression-Discontinuity Analysis
- Regression Point Displacement
- Table of Contents
Fully-functional online survey tool with various question types, logic, randomisation, and reporting for unlimited number of surveys.
Completely free for academics and students .
Inferential Statistics
With inferential statistics, you are trying to reach conclusions that extend beyond the immediate data alone. For instance, we use inferential statistics to try to infer from the sample data what the population might think. Or, we use inferential statistics to make judgments of the probability that an observed difference between groups is a dependable one or one that might have happened by chance in this study. Thus, we use inferential statistics to make inferences from our data to more general conditions; we use descriptive statistics simply to describe what’s going on in our data.
Here, I concentrate on inferential statistics that are useful in experimental and quasi-experimental research design or in program outcome evaluation. Perhaps one of the simplest inferential test is used when you want to compare the average performance of two groups on a single measure to see if there is a difference. You might want to know whether eighth-grade boys and girls differ in math test scores or whether a program group differs on the outcome measure from a control group. Whenever you wish to compare the average performance between two groups you should consider the t-test for differences between groups .
Most of the major inferential statistics come from a general family of statistical models known as the General Linear Model . This includes the t-test, Analysis of Variance (ANOVA), Analysis of Covariance (ANCOVA), regression analysis, and many of the multivariate methods like factor analysis, multidimensional scaling, cluster analysis, discriminant function analysis, and so on. Given the importance of the General Linear Model, it’s a good idea for any serious social researcher to become familiar with its workings. The discussion of the General Linear Model here is very elementary and only considers the simplest straight-line model. However, it will get you familiar with the idea of the linear model and help prepare you for the more complex analyses described below.
One of the keys to understanding how groups are compared is embodied in the notion of the “dummy” variable. The name doesn’t suggest that we are using variables that aren’t very smart or, even worse, that the analyst who uses them is a “dummy”! Perhaps these variables would be better described as “proxy” variables. Essentially a dummy variable is one that uses discrete numbers, usually 0 and 1, to represent different groups in your study. Dummy variables are a simple idea that enable some pretty complicated things to happen. For instance, by including a simple dummy variable in an model, I can model two separate lines (one for each treatment group) with a single equation. To see how this works, check out the discussion on dummy variables .
One of the most important analyses in program outcome evaluations involves comparing the program and non-program group on the outcome variable or variables. How we do this depends on the research design we use. research designs are divided into two major types of designs : experimental and quasi-experimental . Because the analyses differ for each, they are presented separately.
Experimental Analysis
The simple two-group posttest-only randomized experiment is usually analyzed with the simple t-test or one-way ANOVA . The factorial experimental designs are usually analyzed with the Analysis of Variance (ANOVA) Model . Randomized Block Designs use a special form of ANOVA blocking model that uses dummy-coded variables to represent the blocks. The Analysis of Covariance Experimental Design uses, not surprisingly, the Analysis of Covariance statistical model .
Quasi-Experimental Analysis
The quasi-experimental designs differ from the experimental ones in that they don’t use random assignment to assign units (e.g. people) to program groups. The lack of random assignment in these designs tends to complicate their analysis considerably. For example, to analyze the Nonequivalent Groups Design (NEGD) we have to adjust the pretest scores for measurement error in what is often called a Reliability-Corrected Analysis of Covariance model . In the Regression-Discontinuity Design , we need to be especially concerned about curvilinearity and model misspecification. Consequently, we tend to use a conservative analysis approach that is based on polynomial regression that starts by overfitting the likely true function and then reducing the model based on the results. The Regression Point Displacement Design has only a single treated unit. Nevertheless, the analysis of the RPD design is based directly on the traditional ANCOVA model.
When you’ve investigated these various analytic models, you’ll see that they all come from the same family – the General Linear Model . An understanding of that model will go a long way to introducing you to the intricacies of data analysis in applied and social research contexts.
Cookie Consent
Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.
For more information on Conjointly's use of cookies, please read our Cookie Policy .
Which one are you?
I am new to conjointly, i am already using conjointly.

Is it possible any quantitative analysis in a qualitative research?
Most recent answer.

Popular answers (1)

- While Quantitative data collection methods use mathematical calculations to produce numbers , Qualitative data collection methods concern with words and produce descriptions.
- While Quantitative methods are more structured and allow for aggregation and generalization, Qualitative methods are more open and provide for depth and richness.
- Quantitative and qualitative each has their strengths and weaknesses . Sometimes numbers are more useful; other times, narrative (qualitative data) are more useful. Oftentimes, a mix of quantitative and qualitative data provides the most useful information. However, arriving at the correct-manageable mixture of them is not an easy task .
- The purpose of your evaluation. The knowledge gap in an area that needs to be investigated and the goal you seek to achieve have a great effect in determining which methodologies is more convenient. The research problem itself identifies what is problematic about a given topic.
- The respondents (i.e. audience): how can they be reached?
- Resources available: The choice between them ultimately depends upon the available resources like time , money , and analytical tools.
- The needed types of information.
Top contributors to discussions in this field

- Portland State University

- Parthenope University of Naples

- Slovak Society for the Environment. Bratislava • Vice-Rector for Science and Art Catholic University in Ružomberok. Slovak Republic

- University of Kelaniya

- Federation University Australia
Get help with your research
Join ResearchGate to ask questions, get input, and advance your work.
All Answers (29)

Similar questions and discussions
- Asked 31 August 2021

- Asked 1 February 2021

- Asked 13 April 2020

- Asked 31 March 2020

- Asked 17 May 2018

- Doing a MSc literature review evaluating current CBT treatment for social anxiety-
- using sources reviewing treatment and aiming to gather both qualitative and quantitative data to give more valid findings but do not want to go too in depth with Quant stuff as will only be using self report measures etc to support themes that emerge from evaluation? - is it okay to just stick to qualitative data analysis with this in mind or would I need a different approach?
- Any help or advice would be much appreciated!
- Asked 1 March 2016

- Asked 21 June 2015

- Asked 27 July 2024

- Asked 19 July 2024

Related Publications

- Recruit researchers
- Join for free
- Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian Dermatol Online J
- v.10(1); Jan-Feb 2019
Types of Variables, Descriptive Statistics, and Sample Size
Feroze kaliyadan.
Department of Dermatology, King Faisal University, Al Hofuf, Saudi Arabia
Vinay Kulkarni
1 Department of Dermatology, Prayas Amrita Clinic, Pune, Maharashtra, India
This short “snippet” covers three important aspects related to statistics – the concept of variables , the importance, and practical aspects related to descriptive statistics and issues related to sampling – types of sampling and sample size estimation.
What is a variable?[ 1 , 2 ] To put it in very simple terms, a variable is an entity whose value varies. A variable is an essential component of any statistical data. It is a feature of a member of a given sample or population, which is unique, and can differ in quantity or quantity from another member of the same sample or population. Variables either are the primary quantities of interest or act as practical substitutes for the same. The importance of variables is that they help in operationalization of concepts for data collection. For example, if you want to do an experiment based on the severity of urticaria, one option would be to measure the severity using a scale to grade severity of itching. This becomes an operational variable. For a variable to be “good,” it needs to have some properties such as good reliability and validity, low bias, feasibility/practicality, low cost, objectivity, clarity, and acceptance. Variables can be classified into various ways as discussed below.
Quantitative vs qualitative
A variable can collect either qualitative or quantitative data. A variable differing in quantity is called a quantitative variable (e.g., weight of a group of patients), whereas a variable differing in quality is called a qualitative variable (e.g., the Fitzpatrick skin type)
A simple test which can be used to differentiate between qualitative and quantitative variables is the subtraction test. If you can subtract the value of one variable from the other to get a meaningful result, then you are dealing with a quantitative variable (this of course will not apply to rating scales/ranks).
Quantitative variables can be either discrete or continuous
Discrete variables are variables in which no values may be assumed between the two given values (e.g., number of lesions in each patient in a sample of patients with urticaria).
Continuous variables, on the other hand, can take any value in between the two given values (e.g., duration for which the weals last in the same sample of patients with urticaria). One way of differentiating between continuous and discrete variables is to use the “mid-way” test. If, for every pair of values of a variable, a value exactly mid-way between them is meaningful, the variable is continuous. For example, two values for the time taken for a weal to subside can be 10 and 13 min. The mid-way value would be 11.5 min which makes sense. However, for a number of weals, suppose you have a pair of values – 5 and 8 – the midway value would be 6.5 weals, which does not make sense.
Under the umbrella of qualitative variables, you can have nominal/categorical variables and ordinal variables
Nominal/categorical variables are, as the name suggests, variables which can be slotted into different categories (e.g., gender or type of psoriasis).
Ordinal variables or ranked variables are similar to categorical, but can be put into an order (e.g., a scale for severity of itching).
Dependent and independent variables
In the context of an experimental study, the dependent variable (also called outcome variable) is directly linked to the primary outcome of the study. For example, in a clinical trial on psoriasis, the PASI (psoriasis area severity index) would possibly be one dependent variable. The independent variable (sometime also called explanatory variable) is something which is not affected by the experiment itself but which can be manipulated to affect the dependent variable. Other terms sometimes used synonymously include blocking variable, covariate, or predictor variable. Confounding variables are extra variables, which can have an effect on the experiment. They are linked with dependent and independent variables and can cause spurious association. For example, in a clinical trial for a topical treatment in psoriasis, the concomitant use of moisturizers might be a confounding variable. A control variable is a variable that must be kept constant during the course of an experiment.
Descriptive Statistics
Statistics can be broadly divided into descriptive statistics and inferential statistics.[ 3 , 4 ] Descriptive statistics give a summary about the sample being studied without drawing any inferences based on probability theory. Even if the primary aim of a study involves inferential statistics, descriptive statistics are still used to give a general summary. When we describe the population using tools such as frequency distribution tables, percentages, and other measures of central tendency like the mean, for example, we are talking about descriptive statistics. When we use a specific statistical test (e.g., Mann–Whitney U-test) to compare the mean scores and express it in terms of statistical significance, we are talking about inferential statistics. Descriptive statistics can help in summarizing data in the form of simple quantitative measures such as percentages or means or in the form of visual summaries such as histograms and box plots.
Descriptive statistics can be used to describe a single variable (univariate analysis) or more than one variable (bivariate/multivariate analysis). In the case of more than one variable, descriptive statistics can help summarize relationships between variables using tools such as scatter plots.
Descriptive statistics can be broadly put under two categories:
- Sorting/grouping and illustration/visual displays
- Summary statistics.
Sorting and grouping
Sorting and grouping is most commonly done using frequency distribution tables. For continuous variables, it is generally better to use groups in the frequency table. Ideally, group sizes should be equal (except in extreme ends where open groups are used; e.g., age “greater than” or “less than”).
Another form of presenting frequency distributions is the “stem and leaf” diagram, which is considered to be a more accurate form of description.
Suppose the weight in kilograms of a group of 10 patients is as follows:
56, 34, 48, 43, 87, 78, 54, 62, 61, 59
The “stem” records the value of the “ten's” place (or higher) and the “leaf” records the value in the “one's” place [ Table 1 ].
Stem and leaf plot
| 0 | - |
| 1 | - |
| 2 | - |
| 3 | 4 |
| 4 | 3 8 |
| 5 | 4 6 9 |
| 6 | 1 2 |
| 7 | 8 |
| 8 | 7 |
| 9 | - |
Illustration/visual display of data
The most common tools used for visual display include frequency diagrams, bar charts (for noncontinuous variables) and histograms (for continuous variables). Composite bar charts can be used to compare variables. For example, the frequency distribution in a sample population of males and females can be illustrated as given in Figure 1 .

Composite bar chart
A pie chart helps show how a total quantity is divided among its constituent variables. Scatter diagrams can be used to illustrate the relationship between two variables. For example, global scores given for improvement in a condition like acne by the patient and the doctor [ Figure 2 ].

Scatter diagram
Summary statistics
The main tools used for summary statistics are broadly grouped into measures of central tendency (such as mean, median, and mode) and measures of dispersion or variation (such as range, standard deviation, and variance).
Imagine that the data below represent the weights of a sample of 15 pediatric patients arranged in ascending order:
30, 35, 37, 38, 38, 38, 42, 42, 44, 46, 47, 48, 51, 53, 86
Just having the raw data does not mean much to us, so we try to express it in terms of some values, which give a summary of the data.
The mean is basically the sum of all the values divided by the total number. In this case, we get a value of 45.
The problem is that some extreme values (outliers), like “'86,” in this case can skew the value of the mean. In this case, we consider other values like the median, which is the point that divides the distribution into two equal halves. It is also referred to as the 50 th percentile (50% of the values are above it and 50% are below it). In our previous example, since we have already arranged the values in ascending order we find that the point which divides it into two equal halves is the 8 th value – 42. In case of a total number of values being even, we choose the two middle points and take an average to reach the median.
The mode is the most common data point. In our example, this would be 38. The mode as in our case may not necessarily be in the center of the distribution.
The median is the best measure of central tendency from among the mean, median, and mode. In a “symmetric” distribution, all three are the same, whereas in skewed data the median and mean are not the same; lie more toward the skew, with the mean lying further to the skew compared with the median. For example, in Figure 3 , a right skewed distribution is seen (direction of skew is based on the tail); data values' distribution is longer on the right-hand (positive) side than on the left-hand side. The mean is typically greater than the median in such cases.

Location of mode, median, and mean
Measures of dispersion
The range gives the spread between the lowest and highest values. In our previous example, this will be 86-30 = 56.
A more valuable measure is the interquartile range. A quartile is one of the values which break the distribution into four equal parts. The 25 th percentile is the data point which divides the group between the first one-fourth and the last three-fourth of the data. The first one-fourth will form the first quartile. The 75 th percentile is the data point which divides the distribution into a first three-fourth and last one-fourth (the last one-fourth being the fourth quartile). The range between the 25 th percentile and 75 th percentile is called the interquartile range.
Variance is also a measure of dispersion. The larger the variance, the further the individual units are from the mean. Let us consider the same example we used for calculating the mean. The mean was 45.
For the first value (30), the deviation from the mean will be 15; for the last value (86), the deviation will be 41. Similarly we can calculate the deviations for all values in a sample. Adding these deviations and averaging will give a clue to the total dispersion, but the problem is that since the deviations are a mix of negative and positive values, the final total becomes zero. To calculate the variance, this problem is overcome by adding squares of the deviations. So variance would be the sum of squares of the variation divided by the total number in the population (for a sample we use “n − 1”). To get a more realistic value of the average dispersion, we take the square root of the variance, which is called the “standard deviation.”
The box plot
The box plot is a composite representation that portrays the mean, median, range, and the outliers [ Figure 4 ].

The concept of skewness and kurtosis
Skewness is a measure of the symmetry of distribution. Basically if the distribution curve is symmetric, it looks the same on either side of the central point. When this is not the case, it is said to be skewed. Kurtosis is a representation of outliers. Distributions with high kurtosis tend to have “heavy tails” indicating a larger number of outliers, whereas distributions with low kurtosis have light tails, indicating lesser outliers. There are formulas to calculate both skewness and kurtosis [Figures [Figures5 5 – 8 ].

Positive skew

High kurtosis (positive kurtosis – also called leptokurtic)

Negative skew

Low kurtosis (negative kurtosis – also called “Platykurtic”)
Sample Size
In an ideal study, we should be able to include all units of a particular population under study, something that is referred to as a census.[ 5 , 6 ] This would remove the chances of sampling error (difference between the outcome characteristics in a random sample when compared with the true population values – something that is virtually unavoidable when you take a random sample). However, it is obvious that this would not be feasible in most situations. Hence, we have to study a subset of the population to reach to our conclusions. This representative subset is a sample and we need to have sufficient numbers in this sample to make meaningful and accurate conclusions and reduce the effect of sampling error.
We also need to know that broadly sampling can be divided into two types – probability sampling and nonprobability sampling. Examples of probability sampling include methods such as simple random sampling (each member in a population has an equal chance of being selected), stratified random sampling (in nonhomogeneous populations, the population is divided into subgroups – followed be random sampling in each subgroup), systematic (sampling is based on a systematic technique – e.g., every third person is selected for a survey), and cluster sampling (similar to stratified sampling except that the clusters here are preexisting clusters unlike stratified sampling where the researcher decides on the stratification criteria), whereas nonprobability sampling, where every unit in the population does not have an equal chance of inclusion into the sample, includes methods such as convenience sampling (e.g., sample selected based on ease of access) and purposive sampling (where only people who meet specific criteria are included in the sample).
An accurate calculation of sample size is an essential aspect of good study design. It is important to calculate the sample size much in advance, rather than have to go for post hoc analysis. A sample size that is too less may make the study underpowered, whereas a sample size which is more than necessary might lead to a wastage of resources.
We will first go through the sample size calculation for a hypothesis-based design (like a randomized control trial).
The important factors to consider for sample size calculation include study design, type of statistical test, level of significance, power and effect size, variance (standard deviation for quantitative data), and expected proportions in the case of qualitative data. This is based on previous data, either based on previous studies or based on the clinicians' experience. In case the study is something being conducted for the first time, a pilot study might be conducted which helps generate these data for further studies based on a larger sample size). It is also important to know whether the data follow a normal distribution or not.
Two essential aspects we must understand are the concept of Type I and Type II errors. In a study that compares two groups, a null hypothesis assumes that there is no significant difference between the two groups, and any observed difference being due to sampling or experimental error. When we reject a null hypothesis, when it is true, we label it as a Type I error (also denoted as “alpha,” correlating with significance levels). In a Type II error (also denoted as “beta”), we fail to reject a null hypothesis, when the alternate hypothesis is actually true. Type II errors are usually expressed as “1- β,” correlating with the power of the test. While there are no absolute rules, the minimal levels accepted are 0.05 for α (corresponding to a significance level of 5%) and 0.20 for β (corresponding to a minimum recommended power of “1 − 0.20,” or 80%).
Effect size and minimal clinically relevant difference
For a clinical trial, the investigator will have to decide in advance what clinically detectable change is significant (for numerical data, this is could be the anticipated outcome means in the two groups, whereas for categorical data, it could correlate with the proportions of successful outcomes in two groups.). While we will not go into details of the formula for sample size calculation, some important points are as follows:
In the context where effect size is involved, the sample size is inversely proportional to the square of the effect size. What this means in effect is that reducing the effect size will lead to an increase in the required sample size.
Reducing the level of significance (alpha) or increasing power (1-β) will lead to an increase in the calculated sample size.
An increase in variance of the outcome leads to an increase in the calculated sample size.
A note is that for estimation type of studies/surveys, sample size calculation needs to consider some other factors too. This includes an idea about total population size (this generally does not make a major difference when population size is above 20,000, so in situations where population size is not known we can assume a population of 20,000 or more). The other factor is the “margin of error” – the amount of deviation which the investigators find acceptable in terms of percentages. Regarding confidence levels, ideally, a 95% confidence level is the minimum recommended for surveys too. Finally, we need an idea of the expected/crude prevalence – either based on previous studies or based on estimates.
Sample size calculation also needs to add corrections for patient drop-outs/lost-to-follow-up patients and missing records. An important point is that in some studies dealing with rare diseases, it may be difficult to achieve desired sample size. In these cases, the investigators might have to rework outcomes or maybe pool data from multiple centers. Although post hoc power can be analyzed, a better approach suggested is to calculate 95% confidence intervals for the outcome and interpret the study results based on this.
Financial support and sponsorship
Conflicts of interest.
There are no conflicts of interest.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 13: Inferential Statistics
Recall that Matthias Mehl and his colleagues, in their study of sex differences in talkativeness, found that the women in their sample spoke a mean of 16,215 words per day and the men a mean of 15,669 words per day (Mehl, Vazire, Ramirez-Esparza, Slatcher, & Pennebaker, 2007) [1] . But despite this sex difference in their sample, they concluded that there was no evidence of a sex difference in talkativeness in the population. Recall also that Allen Kanner and his colleagues, in their study of the relationship between daily hassles and symptoms, found a correlation of +.60 in their sample (Kanner, Coyne, Schaefer, & Lazarus, 1981) [2] . But they concluded that this finding means there is a relationship between hassles and symptoms in the population. This assertion raises the question of how researchers can say whether their sample result reflects something that is true of the population.
The answer to this question is that they use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research. We begin with a conceptual overview of null hypothesis testing, including its purpose and basic logic. Then we look at several null hypothesis testing techniques for drawing conclusions about differences between means and about correlations between quantitative variables. Finally, we consider a few other important ideas related to null hypothesis testing, including some that can be helpful in planning new studies and interpreting results. We also look at some long-standing criticisms of null hypothesis testing and some ways of dealing with these criticisms.
- Mehl, M. R., Vazire, S., Ramirez-Esparza, N., Slatcher, R. B., & Pennebaker, J. W. (2007). Are women really more talkative than men? Science, 317 , 82. ↵
- Kanner, A. D., Coyne, J. C., Schaefer, C., & Lazarus, R. S. (1981). Comparison of two modes of stress measurement: Daily hassles and uplifts versus major life events. Journal of Behavioural Medicine, 4 , 1–39. ↵
Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Quantitative Data Analysis
3 Univariate Analysis
Roger Clark
Univariate Analyses in Context
This chapter will introduce you to some of the ways researchers use statistics to organize their presentation of individual variables. In Exercise 1 of Introducing Social Data Analysis , you looked at one variable from the General Social Survey (GSS), “sex” or gender, and found that about 54 percent of respondents over the years have been female while about 46 percent have been male. You in fact did an analysis of one variable, sex or gender, and hence did an elementary univariate analysis.
Before we go further into your introduction to univariate analyses, we’d like to provide a somewhat larger context for it. In doing so, we begin with a number of distinctions. One distinction has to do with the number of variables that are involved in an individual analysis. In this book you’ll be exposed to three kinds of analysis: univariate , bivariate and multivariate analyses. Univariate analyses are ones that tell us something about one variable. You did one of these when you discovered that there have been more female than male respondents to the GSS over the years. Bivariate analyses , on the other hand, are analyses that focus on the relationship between two variables. We have just used the GSS source we guided you to (Thomas 2020/2021) to discover that over the years men have been much more likely to work full time than women—roughly 63 percent of male respondents have done so since 1972, while only about 40 percent of female respondents have. This finding results from a bivariate analysis of two variables: gender and work status. Multivariate analyses , then, are ones that permit the examination of the relationship between two variables while investigating the role of other variables as well. Thus, for instance, when we look at the relationship between gender and work status for White Americans and Black Americans separately, we are involving a third variable: race. For White Americans, the GSS tells us, about 63 percent of males have held full time jobs over time, while only about 39 percent of females have done so. For Black Americans, the difference is smaller: 56 percent of males have worked full time, while 44 percent of females have done so. We thus did a multivariate analysis, in which we examined the relationship between gender and work status, while also examining the effect of race on that relationship.
Another important distinction is between descriptive and inferential statistics . This distinction calls into play another: that between samples and populations . Many times researchers will use data that have been collected from a sample of subjects from a larger population . A population is a group of cases about which researchers want to learn something. These cases don’t have to be people; they could be organizations, localities, fire or police departments, or countries. But in case of the GSS, the population of interest is in fact people: all adults in the United States. Very often, it is impractical or undesirable for researchers to gather information about every subject in the population. You can imagine how much time and money it would cost for those who run the GSS, for instance, to contact every adult in the country. So what researchers settle for is information from samples of the larger population. A sample is a number of cases drawn from a larger population. In 2018, for instance, the organization that runs the GSS collected information on just over 2300 adult Americans.
Now we can address the distinction between descriptive and inferential statistics. Descriptive statistics are statistics used to describe a sample. When we learned, for instance, that the GSS reveals that about 63 percent of male respondents worked full time, while about 40 percent of female respondents worked full time, we were getting a description of the sample of adult Americans who had ever participated in the GSS. (And you’d be right if you added that this is a case of bivariate descriptive statistics, since the percentages describe the relationship between two variables in the sample—gender and work status. You’re so smart!) Inferential statistics , on the other hand, are statistics that permit researchers to make inferences about the larger populations from which the sample was drawn. Without going into too much detail here about the requirements for using inferential statistics [1] or how they are calculated, we can tell you that our analysis generated statistics that suggested we’d be on solid ground if we inferred from our sample data that a relationship between gender and work status not only exists in the sample, but also in the larger population of American adults from which the sample was drawn.
In this chapter we will learn something about both univariate descriptive statistics (statistics that describe single variables in a sample) and univariate inferential statistics (statistics that permit inferences about those variables in the larger population from which the sample was drawn).
Levels of Measurement of Variables
Now we can get down to basics. We’ve been throwing around the term variable as if it were second nature to you. (If it is, that’s great. If not, here we go.) A variable is a characteristic that can vary from one subject or case to another or for one case over time. In the case of the GSS data we’ve presented so far, one variable characteristic has been gender or sex. A human adult responding to the GSS may indicate that they are male or female. (They could also identify with other genders, of course, but the GSS hasn’t permitted this so far.) Gender is a variable because it is a characteristic that can vary from one human to another. If we were studying countries, one variable characteristic that might be of interest is the size of the population. Variables, we said, can also vary from one subject over time. Thus, for instance, your age is in one category today, but will be in another next year and in yet another in two years.
The nature of the kinds of categories is crucial to the understanding of the kinds of statistical analysis that can be applied to them. Statisticians refer to these “kinds” of categories as levels of measurement . There are four such levels or kinds of variables: nominal level variables , ordinal level variables , interval level variables , and ratio level variables . And, as you’ll see, the term “level” of measurement makes sense because each level requires that an additional criterion is met for distinguishing it from the previous “level.” The most basic level of measurement is that of the nominal level variable , or a variable whose categories have names. (The word “nominal” has the Latin root nomen , or name.) We say the nominal level is the most basic because every variable is at least a nominal variable. The variable “gender,” when it has the two categories, male and female, has categories that have names and is therefore nominal. So is “religion,” when it has categories like Protestant, Catholic, Jew, Muslim, and other. But so does the variable “age,” when it has categories from 1 and 2 to, potentially, infinity. Each one of categories (1,2,3, etc.) has a name, even though the name is a number. In other words, again, every variable is a nominal level variable. There are some nominal level variables that have the special property of only consisting of two categories, like yes and no or true and false. These variables are called binary variables (also known as dichotomous variables).
To be an ordinal level variable , a variable must have categories can be ordered in some sensible way. (The word “ordinal” has the Latin root ordin alis , or order.) Said another way, an ordinal level variable is a variable whose categories have names and whose categories can be ordered in some sensible way. An example would be the variable “height,” when the categories are “tall,” “medium,” and “short.” Clearly these categories have names (tall, medium and short), but they also can be ordered: tall implies more height than medium, which, in turn, implies more height than short. The variable “gender,” would not qualify as an ordinal level variable, unless one were an inveterate sexist, thinking that one gender is somehow a superior category to the others. Both nominal and ordinal level variables can be called discrete variables , which means they are variables measured using categories rather than numbers.
To be an interval level variable , a variable must be made up of adjacent categories that are a standard distance from one another, typically as measured numerically. Fahrenheit temperatures constitute an interval level variable because the difference between 78 and 79 degrees (1 degree) is seen as the same as the difference between 45 and 46 degrees. But because all those categories (78 degrees, etc.) are named and can be ordered sensibly, it’s pretty easy to see that all interval level variables could be measured at the ordinal level—even while not all nominal and ordinal level variables could be measured at the interval level.
Finally, we come to ratio level variables . Ratio variables are like interval level variables, but with the addition of an absolute zero, a category that indicates the absence of the phenomenon in question. And while some interval level variables cannot be multiplied and divided, ratio level variables can be. Age is an example of a ratio variable because the category, zero, indicates a person or thing has no age at all (while, in contrast, “year of birth” in the calendar system used in the United States does not have an absolute zero, because the year zero is not the absence of any years). But, while interval and ratio variables can be distinguished from each other, we are going to assert that, for the purposes of this book, they are so similar that the distinction isn’t worth insisting upon. As a result, for practical purposes, we could be calling all interval and ratio variables, interval-ratio variables, or simply interval variables. Both ratio and interval level variables can also be referred to as scale or continuous variables, as their (numerical) categories can be placed on a continuous scale.
But what are those practical purposes for which we need to know a variable’s level of measurement? Let’s just see . . .
Measure s of Central Tendency
Roger likes to say, “All statistics are designed with particular levels of measurement in mind.” What’s this mean? [2] Perhaps the easiest way to illustrate is to refer to what statisticians call “ measures of central tendency ” or what we laypersons call “averages.” You may have already learned about three of these averages before: the mean , the median , and the mode . But have you asked yourself why we need three measures of central tendency or average?
The answer lies in the level of measure required by each kind of average. The mean (which is what people most typically refer to when they use the term “average”), you may recall, is the sum of all the categories (or values) in your sample divided by the number of such categories (or values). Now, stop and think: what level of measurement (nominal, ordinal or interval) is required for you to calculate a mean?
If your answer was “interval,” you should give yourself a pat on the back. [3] You need a variable whose categories may legitimately be added to one another in order to calculate a mean. You could do this with the variable “age,” whose categories were 0, 1, 2, 3, etc. But you couldn’t, say, with “height,” if the only categories available to you were tall, medium, and short (if you had actual height in inches or centimeters, of course, that would be a different story).
But if your variable of interest were like that height variable—i.e., an ordinal level variable, statisticians have cooked up another “average” or measure of central tendency just for you: the median . The median is the middle category (or value) when all categories (or values) in the sample are arranged in order. Let’s say your five subjects had heights that were classified as tall, short, tall, medium and tall. If you wanted to calculate the median, you’d first arrange these in order as, for instance, short, medium, tall, tall and tall. You’d then pick the one in the middle—i.e., tall—and that would be your median. Now, stop and think: could you calculate the median of an interval level variable, like the age variable we just talked about?
If your answer was “yes,” you should give yourself a hardy slap on the knee. [4] The median can be used to analyze an interval level variable, as well as ordinal level variables, because all interval level variables are also ordinal. Right?
OK, you say, the mean has been designed to summarize interval level variables and the median has been fashioned to handle ordinal level variables. “I’ll bet,” you say, “the mode is for analyzing nominal level variables.” And you’re right! The mode is the category of a variable in a sample that occurs most frequently. This can be calculated for nominal level variables because nominal level variables, whatever else they have, have categories (with names). Let’s say the four cars you were studying had the colors of blue, red, green and blue. The mode would be blue, because it’s the category of colors that occurs most frequently. Before you take these averages out for a spin, we’d like you to try another question. Can a mode be calculated on an ordinal or an interval level variable?
If you answer “yes,” you should be very proud. Because you’ve probably seen that ordinal and interval variables could also be treated like nominal level variables and therefore can have modes. (That is, categories that occur most frequently). Note, though, that the mode is unlikely to be a helpful measure in instances where continuous variables have many possible numerical values, like annual income in dollars, because in these cases the mode might just be some dollar amount made by three people in a sample where everyone else’s income is unique.
Your Test Drive
| Student | A | B | C | D | E |
| Religion | Catholic | Protestant | Jewish | Catholic | Catholic |
| Height | Tall | Short | Medium | Short | Short |
| Age | 19 | 20 | 19 | 21 | 19 |
How do you know which measure of central tendency or average (mode, median or mean) to use to describe a given variable in a report? The first rule is a negative: do NOT report a measure that is not suitable for your variable’s level of measurement. Thus, you shouldn’t report a mean for the religion or height variables in the “test drive” above, because neither of them is an interval level variable.
You might well ask, “How could I possibly report a mean religion, given the data above?” This is a good question and leads us to mention, in passing, that when researchers set up computer files to help them analyze data, they will almost always code variable categories using numbers so that the computer can recognize them more easily. Coding is the process of assigning observations to categories—and, for computer usage, this often means changing the names of variables categories to numbers. Perhaps you recall doing Exercise 1 at the end of Introducing Social Data Analysis —the one that asked you to determine the percentage of respondents who were female over the years (about 54 percent). Well, to set up the computer to do this analysis, the folks who created the file (and who supplied us with the data) coded males as 1 and females as 2. So the computer was faced with over 34,000 1s and 2s rather than with over 34,000 “males” and “females.” Computers like this kind of help. But computers, while very good at computing, are often a little stupid when it comes to interpreting their computations. [6] So when I went in and asked the computer to add just a few more statistics, including the mean, median and mode, about the sex or gender of GSS respondents, it produced this table. (Don’t worry, I’ll show you how to produce a table like this in Exercise 3 of this chapter.)
| Mean = | 1.54 |
| Std Dev = | .50 |
| Coef var = | .32 |
| Median = | 2.00 |
| Variance = | .25 |
| Min = | 1.00 |
| Mode = | 2.00 |
| Skewness = | -.17 |
| Max = | 2.00 |
| Sum = | 99,993.48 |
| Kurtosis = | -1.97 |
| Range = | 1.00 |
What this table effectively and quickly, tells us is that the mode of “sex” (really gender) is 2, meaning “female.” Part of your job as a social data analyst is to translate codes like this back into English—and report that the mode, here, is “female,” not “2”. But another important part, and something the computer also cannot do, is recognizing the level of measure of the variable concerned—in this case, nominal—and realize which of the reported statistics is relevant given that level. And in terms of “sex,” as reported in Table 1, only you can know how silly it would be to report that the mean “sex” is 1.54 (notice the computer can’t see that silliness) or that its median is 2.00. When Roger was little, [7] Smoky the Bear used to tell kids “Only YOU can prevent forest fires.” But Roger is here to tell you, “Only YOU can prevent statistical reporting travesties.” So, again, you do not want to report statistics that aren’t designed for the level of measure of your variables.
In general, though, when you ARE dealing with an interval variable, like age in years, you really have three choices about which to report: the mean, the median and the mode. For the moment, we’re going to recommend that, in such case, you might consider that the reading public is likely to be most familiar with the mean and, for that reason, you might report the mean. (We’ll get to qualifications of that recommendation a little later.)
Measures of central tendency are often useful for summarizing variables, but they can sometimes be misleading. Roger just [8] Googled the average life expectancy for men in the United States and discovered it was about 76.5 years. (Pretty clearly a mean, not a mode or median, right?) At this sitting, he is about 71.5 years old. Does this mean he has exactly 5 years left of life to live? Well, probably not. Given his health, educational level, etc., he’s likely to live considerably longer…unless COVID-19 gets him tomorrow. The point is that for life expectancy, as for other variables, there’s variation around the average. And sometimes knowing something about that variation is at least as important as the average itself—sometimes more important.
We can learn a lot about a variable, for instance, simply by showing how its cases are distributed over its categories in a sample. Exercise 1 at the end of Introducing Social Data Analysis actually told you the modal gender of respondents to the GSS survey. (“Modal” is the adjectival form of mode.) Do you recall what that was? It was “female,” right? What this tells you is that the “average” respondent over the years has been a female. But the mode, being what it is, doesn’t tell you whether 100 percent of respondents were female or 50.1 percent were female. And that’s an important difference.
One of the most commonly used ways of showing variation is what’s called a frequency distribution . A frequency distribution shows the number of times cases fall into each category in a sample. I’ve just called up the table you looked at in Exercise 1 of Introducing Social Data Analysis and plunked it down here as Table 2. What this table shows is that while about 35,179 females had participated in the GSS since 1972, 29,635 males had done so as well. The table further tells us that while about 54 percent of the sample is female, about 46 percent has been male. The distribution has been much closer to 50-50 than 100-0. And this extra information about the variable is a significant addition to the fact that modal “sex” was female.
| Cells contain: – -Weighted N | ||
| 1: MALE | | |
| 2: FEMALE | | |
|
| | |
“Sex” is a nominal level variable, and frequency distributions have been designed for displaying the variation of nominal level variables. But, of course, because ordinal and interval variables are also nominal level variables, frequency distributions can be used to describe their variation as well. And this often makes sense with ordinal level variables. Thus, for instance, we used a frequency distribution of respondents’ confidence in the military (“conarm”) to show that there was relatively little variation in Americans’ confidence in that institution in 2018 (Table 3, below). Almost 61 percent of respondents said they had a “great deal of confidence” in the military that year, while only about 39 percent said they had “only some” or “hardly any” confidence. In other words, at least in comparison with the variation in “sex,” variation in confidence in the military, which, after all, has three categories, seems limited. In other words, this kind of confidence seems more concentrated in one category (“great deal of confidence”) than you might expect.
Quiz at the End of the Paragraph : Can you see what the median and the mode of confidence in the military was?
Bonus Trick Question : What was its mean?
| Cells contain: – -Weighted N | ||
|
(Confidence in the U.S. Military) | 1: A GREAT DEAL | |
| 2: ONLY SOME | | |
| 3: HARDLY ANY | | |
|
| | |
| Mean = | 1.46 | Std Dev = | .62 |
| Coef var = | .43 |
| Median = | 1.00 | Variance = | .39 |
| Min = | 1.00 |
| Mode = | 1.00 | Skewness = | 1.00 | Max = | 3.00 | |
| Sum = | 2,273.32 | Kurtosis = | -.06 |
| Range = | 2.00 |
Measures of Variation for Interval Level Variables
Looking at frequency distributions is a pretty good way of getting a sense of the variation in nominal and ordinal variables. But it would be a fairly awkward way of doing so for interval variables, many of which, if you think about it, would have many categories. (Can you imagine a frequency distribution for the variable “age” of respondents in the GSS?) Statisticians have actually given us some pretty elegant ways of dealing with the description of variation in interval variables and we’d now like to illustrate them with simple examples.
Roger’s daughter, Wendy, was a day care provider for several years and could report that variation in the ages of preschool children made a tremendous difference in the kinds of things you can do with them. Imagine, if you will, that you had two groups of four preschool children, one of which had four 3-year-olds in it and one of which had two 5-year-olds and two 1-year-olds. Can you calculate the mean age of each group?
If you found that the mean age of both groups was 3 years old, you did a fine job. Now, if you were inclined to think that any two groups with the same mean age were likely to be similar, think of these two from a day care provider’s point of view. Figuring out what to do for a day with two 1-year-olds and two 5-year-olds would be a much more daunting task than planning for four 3-year-olds. Wouldn’t it?
Statisticians have given us one particularly simple measure of spread or variation for interval level variables: the range . The range is simply the highest category in your sample minus the lowest category. For the group with four 3-year-olds, the range would be (3-3=) zero years. There is no variation in age for this group. For the group with two 1-year-olds and two 5-year-olds, the range would be (5-1=) four years. A substantial, and important difference, again especially if you, like my daughter, were a day care provider. Means don’t always tell the whole story, do they?
Perhaps the more commonly used statistic for describing the variation or spread of an interval level variable, however, is the standard deviation . The range only gives you a sense of how spread out the extreme values or categories are in your sample. The standard deviation is a measure of variation that takes into account every value’s distance from the sample mean. The usefulness of such a measure can be illustrated with another simple example. Imagine, for instance, that your two groups of preschool children had the following ages: 1, 1, 5, 5, on the one hand, and 1, 3, 3, and 5, on the other.
The mean of these two groups is 3 years and the range is 4 years. But are they identical? No. You may notice that each of the individual ages in the first group is a “distance” of 2 away from the mean of 3. (The two 1s are each 2 away from 3 and the two 5s are also 2 away from 3.) So the average “distance” of each age from the mean is 2 for group 1. But that’s not true for the second group. The 1 and the 5 are both 2 away from the mean of 3, but the two 3s are both no distance away. So the average distance of ages from the mean in this group is something less than 2. Hence, the average distance of ages from the mean in the first group is larger than the average distance in the second group. The standard deviation is a way of capturing a difference like this—one that is not captured by the range.
It does this by using a formula that essentially adds the individual “distances” of categories or values from the mean and then divides that number by the categories. We think of it as being very similar to the computation of the mean itself: a sum divided by the number of cases involved. The computational formula is:
[latex]SD_{sample} = \sqrt{\frac{ \sum_{i=1}^N (x - \overline{x})^2} {N-1} }[/latex] where [latex]SD_{sample}[/latex] stands for the standard deviation [latex]\sqrt{~^{~}}[/latex] stands for the square root of the entire expression that follows [latex]\sum_{i=1}^N[/latex] means to add up the sequence of numbers produced by the expression that follows [latex]x[/latex] stands for each value of category in the sample [latex]\overline{x}[/latex] stands for the sample mean [latex]N[/latex] stands for the number of sample cases
The formula may look daunting, but it’s not very difficult to compute with just a few cases—and we’ll never ask you to use anything other than a computer to compute the standard deviation with more cases. Note that to calculate the standard deviation for an entire population, rather than a sample, we use N rather than N-1 in the denominator. And also note that the numerator—[latex]Var(X)=\sum_{i=1}^N (x - \overline{x})^2[/latex]—is referred to as the variance .
Notice first that the formula asks you to compute the sample mean. For the second sample of ages above—the one with ages 1, 3, 3, 5—the mean is 3. It then asks you to take the difference between each category in the sample and the mean and square the differences. 1-3, for instance, is -2 and its square is 4. 3-3 is 0 and its square is 0. And 5-3 is 2 and its square is 4. The formula then asks you to add these squared values up: 4 0 0 4=8. Then it says to divide by the number of cases, minus 1: 3. 8/3=2.67. It then asks you to take the square root of 2, or about 1.6. So the standard deviation of this sample is about 1.6 years.
Can you calculate the standard deviation for the second sample of ages above: 1, 1, 5, 5?
Did you get 2.3? If so, give yourself another pat on the back. [9]
Measures of Deviation from the Normal Distribution
We’ve suggested that, other things being equal, the mean is a good way of describing the central tendency or average of an interval level variable. But other things aren’t always equal. The mean is an excellent measure of central tendency, for instance, when the interval level variable conforms to what is called a normal distribution . A normal distribution of a variable is one that is symmetrical and bell-shaped (otherwise called a bell curve ), like the one in Figure 2.1. This image suggests what is true when the distribution of a variable is normally distributed: that 68 percent of cases fall within one standard deviation on either side of the mean; that 95 percent of the cases fall within two standard deviations on either side; and that 99.7 percent of the cases fall within three standard deviations on either side. Note that the symbol [latex]\sigma[/latex] is used to indicate standard deviation in many statistical contexts.
One example that is frequently cited as a normally distributed variable is height. For American men, the average height in 2020 is about 69 inches, [10] where “average” here refers to the mean, the median and the mode, if, in fact, height is normally distributed. The peak of the curve (can you see it in your mind?) would be at 69 inches, which would be the most frequently occurring category, the one in the middle of the distribution of categories and the arithmetic mean.
But what happens when a variable is not normally distributed? We asked the Social Data Archive to use GSS data from 2010 to tell us what distribution of the number of children respondents had looked like, and we got these results (see Table 4):
| Mean = | 1.91 |
| Std Dev = | 1.73 | Coef var = | .91 | |
| Median = | 2.00 |
| Variance = | 2.99 | Min = | .00 | |
| Mode = | .00 |
| Skewness = | 1.05 | Max = | 8.00 | |
| Sum = | 3,894.30 |
| Kurtosis = | 1.39 | Range = | 8.00 | |
As you might have expected, the greatest number of respondents said they had zero, one or two children. But, then the number of children tails off pretty quickly as you get into categories that represent respondents with 3 or more children. This variable, then, is not normally distributed. Most of the cases are concentrated in the lowest categories. When an interval level variable looks that this, it is said to have right, or positive skewness, and this is reflected in the report that “number of children” has a skewness of positive 1.05. Skewness refers to an asymmetry in a distribution in which a curve is distorted either to the left or the right. The skewness statistic can take on values from negative infinity to positive infinity, with positive values indicating right skewness (with “tails” to the right) and negative values indicating left skewness (when “tails” are to the left). A skewness statistic of zero would indicate that a variable is perfectly symmetrical.
Our rule of thumb is that when the skewness statistic gets near to 1 or near -1, the variable has more than enough skewness (either to the right or to the left) to be disqualified as a normally distributed variable. And in such cases, it’s probably useful to report both the mean and the median as measures of central tendency, since the relationship of the two will give some idea to readers of the nature of the variable’s skewness. If the median is greater than the mean (as it is in the case of “number of children”), it’s a sign that the author means to convey that the variable is right skewed. If it’s less than the mean, the implication is that it’s left skewed.
Kurtosis refers to how sharp the peak of a frequency distribution is. If the peak is too pointed to be a normal curve, it is said to have positive kurtosis (or “ leptokurtosis ”). The kurtosis statistic of “number of children” is 1.39, indicating that the variable’s distribution has positive kurtosis (or leptokurtosis). If the peak of a distribution is too flat to be normally distributed, it is said to have negative kurtosis (or platykurtosis ), as seen in Figure 2.3.
A rule of thumb for the kurtosis statistic: if it gets near to 1 or near -1, the variable has more than enough kurtosis (either positive or negative) to be disqualified as a normally distributed variable.
For a fascinating, personal lecture about the importance of being wary about reports using only measures of central tendency or average (e.g., means and medians), however, we encourage you to listen to the following talk by Stephen Jay Gould:
A Word About Univariate Inferential Statistics
Up to this point, we’ve only talked about univariate descriptive statistics, or statistics that describe one variable in a sample. When we learned that 54 percent of GSS respondents over the years have been women, we were simply learning about the (large) sample of people who have responded to the GSS over the years. And when we learned that the mean number of children that respondents had in 2010 was about 1.9 and the median was 2.0, those too were descriptions of the sample that year. One of the purposes of sampling, though, is that it can provide us some insight into the population from which the sample was drawn. In order to make inferences about such populations from sample data we need to use inferential statistics. Inferential statistics , as we said before, are statistics that permit researchers to make inferences about the larger population from which a sample is drawn.
We’ll be spending more time on inferential statistics in other chapters, but now we’d like to introduce you a statistical concept that frequently comes up in relation to political polls: margin of error . To appreciate the concept of the margin of error, we need to understand the difference between two important concepts: statistics and parameters . A statistic is a description of a variable (or the relationship between variables) in a sample. The mean, median, mode, range, standard deviation and skewness are all types of statistics. A parameter , on the other hand, is a description of a variable (or the relationship between variables) in a population; many (but not all) of the same tools used as statistics when analyzing data from samples can be used as parameters when analyzing data on populations. A margin of error , then, is a suggestion of how far away from the actual population parameter a statistic is likely to be. Thus political polling can tell you precisely what percentage of the sample say they are going to vote for a candidate, but it can’t tell you precisely what percentage would say the same thing in the larger population from which the sample was drawn.
BUT, when a sample is a probability sample of the larger population, we can estimate how close the population percentage is likely to be to the sample percentage. A full discussion of the different kinds of samples is beyond the scope of this book, but let’s just say that a probability sample is one that has been drawn to give every member of the population a known (non-zero) chance of inclusion. Inferential statistics of all kinds assume that one is dealing with a probability sample of the larger population to which one would like to generalize (though, sometimes, inferential statistics are calculated even when this fundamental assumption of inferential statistics has not been met). [11]
Most frequently, a margin of error is a statement of the range around the sample percentage in which there is a 95 percent chance that the population percentage will fall. The pre-election polls before the 2016 election are frequently criticized for how badly they got it wrong when they predicted Hillary Clinton would get a higher percentage of the vote than Donald Trump—and win the election. But in fact most of the national polls came remarkably close to predicting the election outcome perfectly. Thus, for instance, an ABC News/Washington Post poll, collected between November 3 rd and November 6 th (two days before the election), and involving a sample of 2,220, predicted that Clinton would get 49 percent of the vote, plus or minus 2.5 percentage points (meaning that she’d likely get somewhere between 46.5 percent and 51.5 percent of the vote), and that Trump would get 46 percent, plus or minus 2.5 percentage points (meaning that he’d likely get somewhere between 43.5 percent and 48.5 percent of the vote). The margin of error in this poll, then, was plus or minus 2.5 percentage points. And, in fact, Clinton won 48.5 percent of the actual vote (well within the margin of error) and Trump won 46.4 percent (again, well within the margin of error) (CNN Politics, 2020). This is just one poll that got the election precisely right with respect to the total vote (if not the crucial electoral vote) count in advance of the election.
We haven’t shown you how to calculate a margin of error here but, as you’ll see in Exercise 4 at the end of the chapter, they are not hard to get a computer to spit out. One thing to keep in mind is that the size of a margin of error is a function of the size of the sample: the larger the sample, the smaller the margin of error. In fact all inferences using inferential statistics become more accurate as the sample size increases.
So, welcome to the world of univariate statistics! Now let’s try some exercises to see how they work.
- Which of the measures of central tendency has been designed for nominal level variables? For ordinal level variables? For interval level variables? Why can all three measures be applied to interval level variables?
- Which way of showing the variation of nominal and ordinal level variables have we examined in this chapter? What measures of variation for interval level variables have we encountered?
- Return to the Social Data Archive we explored in Exercise 1 of Introducing Social Data Analysis . The data, again, are available at https://sda.berkeley.edu/ . Again, go down to the second full paragraph and click on the “SDA Archive” link you’ll find there. Then scroll down to the section labeled “General Social Surveys” and click on the first link there: General Social Survey (GSS) Cumulative Datafile 1972-2018 release. Now type “religion” in the row box, hit “output options,” click on “summary statistics,” then click on “run the table.” See if you can answer these questions:
- What level of measurement best characterizes “religion”? What is this variable measuring?
- What’s the only measure of central tendency you can report for “religion”? Report this measure, in English, not as a number.
- What’s a good way you can describe ”religion”’s variation? Describe its variation.
Now type “happy” in the row box, hit “output options,” click on “summary statistics,” then click on “run the table.” See if you can answer these questions:
- What level of measurement best characterizes “happy”? What is this variable measuring?
- What are the only measures of central tendency you can report for “happy”? Report these measures, in English, not as a number.
- What’s a good way you can use to describe “happy”’s variation? Describe its variation.
Now type “age” in the row box, hit “output options,” click on “summary statistics,” then click on “run the table.” See if you can answer these questions:
- What level of measure best describes “age”? What is this variable measuring?
- What are all the measures of central tendency you could report for “age”? Report these measures, in English, not simply as numbers.
- What are two good statistics for describing “age”’s variation? Describe its variation.
- Is it your sense that “age” is essentially normally distributed? Why or why not? (What statistics did you check for this?)
- Return to the Social Data Archive. The data, again, are available at https://sda.berkeley.edu/ (You may have to copy and paste this address to request the website.) Again, go down to the second full paragraph and click on the “SDA Archive” link you’ll find there. Then scroll down to the section labeled “American National Election Studies (ANES)” and hit on the first link there: American National Election Study (ANES) 2016. These data come from a survey done after the 2016 election. Type “Trumpvote” in the row, hit “output options,” and hit “confidence intervals,” then hit “run table.” What percentage of respondents, after the election, said they had voted for Trump? What was the “95 percent” confidence interval for this percentage? Check the end of this chapter for the actual percentage of the vote that Trump got. Does it fall within this interval?
Media Attributions
- Standard_deviation_diagram.svg © M. W. Toews is licensed under a CC BY (Attribution) license
- Negative Skew © Diva Dugar adapted by Roger Clark is licensed under a CC BY-SA (Attribution ShareAlike) license
- Kurtosis © Mikaila Mariel Lemonik Arthur
- Note that you can use many statistical methods to analyze data about populations, there are some differences in how they are employed, as will be discussed later in this chapter. ↵
- Besides the fact that he’s getting increasingly senile? ↵
- Something that’s increasingly difficult for Roger to do as he gets up in years. ↵
- Unless you’ve got arthritis there like you know who. ↵
- The mode of religion is Catholic. No other average is applicable. The median of height is short, and so is the mode. The mean of height can’t be calculated. The mean height is 19.6. Its median is 19, as is its mode. ↵
- No offense to you, my faithful laptop, without which I couldn’t bring you, my readers, this cautionary tale. ↵
- Many years ago. ↵
- You already know Roger can’t do this for himself. ↵
- 5 feet, 9 inches ↵
- And we hope you’ll always say “naughty, naughty,” when you know this has been done. ↵
Quantitative analyses that tell us about one variable, like the mean, median, or mode.
Quantitative analyses that tell us about the relationship between two variables.
Quantitative analyses that explores relationships involving more than two variables or examines the impact of other variables on a relationship between two variables.
Statistics used to describe a sample.
Statistics that permit researchers to make inferences (or reasoned conclusions) about the larger populations from which a sample has been drawn.
A subset of cases drawn or selected from a larger population.
A group of cases about which researchers want to learn something; generally, members of a population share common characteristics that are relevant to the research, such as living in a certain area, sharing a certain demographic characteristic, or having had a common experience.
A characteristic that can vary from one subject or case to another or for one case over time within a particular research study.
Classification of variables in terms of the precision or sensitivity in how they are recorded.
A variable whose categories have names that do not imply any order.
Consisting of only two options. Also known as dichotomous.
Consisting of only two options. Also known as binary.
A variable with categories that can be ordered in a sensible way.
A variable measured using categories rather than numbers, including binary/dichotomous, nominal, and ordinal variables.
A variable with adjacent, ordered categories that are a standard distance from one another, typically as measured numerically.
A numerical variable with an absolute zero which can also be multiplied and divided.
A variable measured using numbers, not categories, including both interval and ratio variables. Also called a continuous variable.
A variable measured using numbers, not categories, including both interval and ratio variables. Also called a scale variable.
A measure of the value most representative of an entire distribution of data.
The sum of all the values in a list divided by the number of such values.
The middle value when all values in a list are arranged in order.
The category in a list that occurs most frequently.
The process of assigning observations to categories.
An analysis that shows the number of cases that fall into each category of a variable.
The highest category in a list minus the lowest category.
A measure of variation that takes into account every value’s distance from the sample mean.
A distribution of values that is symmetrical and bell-shaped.
A graph showing a normal distribution—one that is symmetrical with a rounded top that then falls away towards the extremes in the shape of a bell
An asymmetry in a distribution in which a curve is distorted either to the left or the right, with positive values indicating right skewness and negative values indicating left skewness.
How sharp the peak of a frequency distribution is. If the peak is too pointed to be a normal curve, it is said to have positive kurtosis (or “leptokurtosis”). If the peak of a distribution is too flat to be normally distributed, it is said to have negative kurtosis (or platykurtosis).
The characteristic of a distribution that is too pointed to be a normal curve, indicated by a positive kurtosis statistic.
The characteristic of a distribution that is too flat to be a normal curve, indicated by a negative kurtosis statistic.
Quantitative measures of data from a sample.
A quantitative measure of data from a population.
A suggestion of how far away from the actual population parameter a sample statistic is likely to be.
A sample that has been drawn to give every member of the population a known (non-zero) chance of inclusion.
Social Data Analysis Copyright © 2021 by Roger Clark is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Quantitative Data Analysis: Everything You Need to Know
11 min read

Does the thought of quantitative data analysis bring back the horrors of math classes? We get it.
But conducting quantitative data analysis doesn’t have to be hard with the right tools. Want to learn how to turn raw numbers into actionable insights on how to improve your product?
In this article, we explore what quantitative data analysis is, the difference between quantitative and qualitative data analysis, and statistical methods you can apply to your data. We also walk you through the steps you can follow to analyze quantitative information, and how Userpilot can help you streamline the product analytics process. Let’s get started.
- Quantitative data analysis is the process of using statistical methods to define, summarize, and contextualize numerical data.
- Quantitative analysis is different from a qualitative one. The first deals with numerical data and focuses on answering “what,” “when,” and “where.” However, a qualitative analysis relies on text, graphics, or videos and explores “why” and “how” events occur.
- Pros of quantitative data analysis include objectivity, reliability, ease of comparison, and scalability.
- Cons of quantitative metrics include the data’s limited context and inflexibility, and the need for large sample sizes to get statistical significance.
- The methods for analyzing quantitative data are descriptive and inferential statistics.
- Choosing the right analysis method depends on the type of data collected and the specific research questions or hypotheses.
- These are the steps to conduct quantitative data analysis: 1. Defining goals and KPIs . 2. Collecting and cleaning data. 3. Visualizing the data. 4. Identifying patterns . 5. Sharing insights. 6. Acting on findings to improve decision-making.
- With Userpilot , you can auto-capture in-app user interactions and build analytics dashboards . This tool also lets you conduct A/B and multivariate tests, and funnel and cohort analyses .
- Gather and visualize all your product analytics in one place with Userpilot. Get a demo .
Try Userpilot and Take Your Product Experience to the Next Level
- 14 Day Trial
- No Credit Card Required
What is quantitative data analysis?
Quantitative data analysis is about applying statistical analysis methods to define, summarize, and contextualize numerical data. In short, it’s about turning raw numbers and data into actionable insights.
The analysis will vary depending on the research questions and the collected data (more on this below).
Quantitative vs qualitative data analysis
The main difference between these forms of analysis lies in the collected data. Quantitative data is numerical or easily quantifiable. For example, the answers to a customer satisfaction score (CSAT) survey are quantitative since you can count the number of people who answered “very satisfied”.
Qualitative feedback , on the other hand, analyzes information that requires interpretation. For instance, evaluating graphics, videos, text-based answers, or impressions.
Another difference between quantitative and qualitative analysis is the questions each seeks to answer. For instance, quantitative data analysis primarily answers what happened, when it happened, and where it happened. However, qualitative data analysis answers why and how an event occurred.
Quantitative data analysis also looks into identifying patterns , drivers, and metrics for different groups. However, qualitative analysis digs deeper into the sample dataset to understand underlying motivations and thinking processes.
Pros of quantitative data analysis
Quantitative or data-driven analysis has advantages such as:
- Objectivity and reliability. Since quantitative analysis is based on numerical data, this reduces biases and allows for more objective conclusions. Also, by relying on statistics, this method ensures the results are consistent and can be replicated by others, making the findings more reliable.
- Easy comparison. Quantitative data is easily comparable because you can identify trends , patterns, correlations, and differences within the same group and KPIs over time. But also, you can compare metrics in different scales by normalizing the data, e.g., bringing ratios and percentages into the same scale for comparison.
- Scalability. Quantitative analysis can handle large volumes of data efficiently, making it suitable for studies involving large populations or datasets. This makes this data analysis method scalable. Plus, researchers can use quantitative analysis to generalize their findings to broader populations.
Cons of quantitative data analysis
These are common disadvantages of data-driven analytics :
- Limited context. Since quantitative data looks at the numbers, it often strips away the data from the context, which can show the underlying reasons behind certain trends. This limitation can lead to a superficial understanding of complex issues, as you often miss the nuances and user motivations behind the data points.
- Inflexibility. When conducting quantitative research, you don’t have room to improvise based on the findings. You need to have predefined hypotheses, follow scientific methods, and select data collection instruments. This makes the process less adaptable to new or unexpected findings.
- Large sample sizes necessary. You need to use large sample sizes to achieve statistical significance and reliable results when doing quantitative analysis. Depending on the type of study you’re conducting, gathering such extensive data can be resource-intensive, time-consuming, and costly.
Quantitative data analysis methods
There are two statistical methods for reviewing quantitative data and user analytics . However, before exploring these in-depth, let’s refresh these key concepts:
- Population. This is the entire group of individuals or entities that are relevant to the research.
- Sample. The sample is a subset of the population that is actually selected for the research since it is often impractical or impossible to study the entire population.
- Statistical significance. The chances that the results gathered after your analysis are realistic and not due to random chance.
Here are methods for analyzing quantitative data:
Descriptive statistics
Descriptive statistics, as the name implies, describe your data and help you understand your sample in more depth. It doesn’t make inferences about the entire population but only focuses on the details of your specific sample.
Descriptive statistics usually include measures like the mean, median, percentage, frequency, skewness, and mode.
Inferential statistics
Inferential statistics aim to make predictions and test hypotheses about the real-world population based on your sample data.
Here, you can use methods such as a T-test, ANOVA, regression analysis, and correlation analysis.
Let’s take a look at this example. Through descriptive statistics, you identify that users under the age of 25 are more likely to skip your onboarding. You’ll need to apply inferential statistics to determine if the result is statistically significant and applicable to your entire ’25 or younger’ population.
How to choose the right method for your quantitative data analysis
The type of data that you collect and the research questions that you want to answer will impact which quantitative data analysis method you choose. Here’s how to choose the right method:
Determine your data type
Before choosing the quantitative data analysis method, you need to identify which group your data belongs to:
- Nominal —categories with no specific order, e.g., gender, age, or preferred device.
- Ordinal —categories with a specific order, but the intervals between them aren’t equal, e.g., customer satisfaction ratings .
- Interval —categories with an order and equal intervals, but no true zero point, e.g., temperature (where zero doesn’t mean “no temperature”).
- Ratio —categories with a specific order, equal intervals, and a true zero point, e.g., number of sessions per user .
Applying any statistical method to all data types can lead to meaningless results. Instead, identify which statistical analysis method supports your collected data types.
Consider your research questions
The specific research questions you want to answer, and your hypothesis (if you have one) impact the analysis method you choose. This is because they define the type of data you’ll collect and the relationships you’re investigating.
For instance, if you want to understand sample specifics, descriptive statistics—such as tracking NPS —will work. However, if you want to determine if other variables affect the NPS, you’ll need to conduct an inferential analysis.
The overarching questions vary in both of the previous examples. For calculating the NPS, your internal research question might be, “Where do we stand in customer loyalty ?” However, if you’re doing inferential analysis, you may ask, “How do various factors, such as demographics, affect NPS?”
6 steps to do quantitative data analysis and extract meaningful insights
Here’s how to conduct quantitative analysis and extract customer insights :
1. Set goals for your analysis
Before diving into data collection, you need to define clear goals for your analysis as these will guide the process. This is because your objectives determine what to look for and where to find data. These goals should also come with key performance indicators (KPIs) to determine how you’ll measure success.
For example, imagine your goal is to increase user engagement. So, relevant KPIs include product engagement score , feature usage rate , user retention rate, or other relevant product engagement metrics .
2. Collect quantitative data
Once you’ve defined your goals, you need to gather the data you’ll analyze. Quantitative data can come from multiple sources, including user surveys such as NPS, CSAT, and CES, website and application analytics , transaction records, and studies or whitepapers.
Remember: This data should help you reach your goals. So, if you want to increase user engagement , you may need to gather data from a mix of sources.
For instance, product analytics tools can provide insights into how users interact with your tool, click on buttons, or change text. Surveys, on the other hand, can capture user satisfaction levels . Collecting a broad range of data makes your analysis more robust and comprehensive.

3. Clean and visualize your data
Raw data is often messy and contains duplicates, outliers, or missing values that can skew your analysis. Before making any calculations, clean the data by removing these anomalies or outliers to ensure accurate results.
Once cleaned, turn it into visual data by using different types of charts , graphs, or heatmaps . Visualizations and data analytics charts make it easier to spot trends, patterns, and anomalies. If you’re using Userpilot, you can choose your preferred visualizations and organize your dashboard to your liking.
4. Identify patterns and trends
When looking at your dashboards, identify recurring themes, unusual spikes, or consistent declines that might indicate data analytics trends or potential issues.
Picture this: You notice a consistent increase in feature usage whenever you run seasonal marketing campaigns . So, you segment the data based on different promotional strategies. There, you discover that users exposed to email marketing campaigns have a 30% higher engagement rate than those reached through social media ads.
In this example, the pattern suggests that email promotions are more effective in driving feature usage.
If you’re a Userpilot user, you can conduct a trend analysis by tracking how your users perform certain events.

5. Share valuable insights with key stakeholders
Once you’ve discovered meaningful insights, you have to communicate them to your organization’s key stakeholders. Do this by turning your data into a shareable analysis report , one-pager, presentation, or email with clear and actionable next steps.
Your goal at this stage is for others to view and understand the data easily so they can use the insights to make data-led decisions.
Following the previous example, let’s say you’ve found that email campaigns significantly boost feature usage. Your email to other stakeholders should strongly recommend increasing the frequency of these campaigns and adding the supporting data points.
Take a look at how easy it is to share custom dashboards you built in Userpilot with others via email:
6. Act on the insights
Data analysis is only valuable if it leads to actionable steps that improve your product or service. So, make sure to act upon insights by assigning tasks to the right persons.
For example, after analyzing user onboarding data, you may find that users who completed the onboarding checklist were 3x more likely to become paying customers ( like Sked Social did! ).
Now that you have actual data on the checklist’s impact on conversions, you can work on improving it, such as simplifying its steps, adding interactive features, and launching an A/B test to experiment with different versions.
How can Userpilot help with analyzing quantitative data
As you’ve seen throughout this article, using a product analytics tool can simplify your data analysis and help you get insights faster. Here are different ways in which Userpilot can help:
Automatically capture quantitative data
Thanks to Userpilot’s new auto-capture feature, you can automatically track every time your users click, write a text, or fill out a form in your app—no engineers or manual tagging required!
Our customer analytics platform lets you use this data to build segments, trigger personalized in-app events and experiences, or launch surveys.
If you don’t want to auto-capture raw data, you can turn this functionality off in your settings, as seen below:

Monitor key metrics with customizable dashboards for real-time insights
Userpilot comes with template analytics dashboards , such as new user activation dashboards or customer engagement dashboards . However, you can create custom dashboards and reports to keep track of metrics that are relevant to your business in real time.
For instance, you could build a customer retention analytics dashboard and include all metrics that you find relevant, such as customer stickiness , NPS, or last accessed date.
Analyze experiment data with A/B and multivariate tests
Userpilot lets you conduct A/B and multivariate tests , either by following a controlled or a head-to-head approach. You can track the results on a dashboard.
For example, let’s say you want to test a variation of your onboarding flow to determine which leads to higher user activation .
You can go to Userpilot’s Flows tab and click on Experiments. There, you’ll be able to select the type of test you want to run, for instance, a controlled A/B test , build a new flow, test it, and get the results.

Use quantitative funnel analysis to increase conversion rates
With Userpilot, you can track your customers’ journey as they complete actions and move through the funnel. Funnel analytics give you insights into your conversion rates and conversion times between two events, helping you identify areas for improvement.
Imagine you want to analyze your free-to-paid conversions and the differences between devices. Just by looking at the graphic, you can draw some insights:
- There’s a significant drop-off between steps one and two, and two and three, indicating potential user friction .
- Users on desktops convert at higher rates than those on mobile or unspecified devices.
- Your average freemium conversion time is almost three days.

Leverage cohort analysis to optimize retention
Another Userpilot functionality that can help you analyze quantitative data is cohort analysis . This powerful tool lets you group users based on shared characteristics or experiences, allowing you to analyze their behavior over time and identify trends, patterns, and the long-term impact of changes on user behavior.
For example, let’s say you recently released a feature and want to measure its impact on user retention. Via a cohort analysis, you can group users who started using your product after the update and compare their retention rates to previous cohorts.
You can do this in Userpilot by creating segments and then tracking user segments ‘ retention rates over time.

Check how many users adopted a feature with a retention table
In Userpilot, you can use retention tables to stay on top of feature adoption . This means you can track how many users continue to use a feature over time and which features are most valuable to your users. The video below shows how to choose the features or events you want to analyze in Userpilot.
As you’ve seen, to conduct quantitative analysis, you first need to identify your business and research goals. Then, collect, clean, and visualize the data to spot trends and patterns. Lastly, analyze the data, share it with stakeholders, and act upon insights to build better products and drive customer satisfaction.
To stay on top of your KPIs, you need a product analytics tool. With Userpilot, you can automate data capture, analyze product analytics, and view results in shareable dashboards. Want to try it for yourself? Get a demo .
Leave a comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.

Get The Insights!
The fastest way to learn about Product Growth,Management & Trends.
The coolest way to learn about Product Growth, Management & Trends. Delivered fresh to your inbox, weekly.
The fastest way to learn about Product Growth, Management & Trends.
You might also be interested in ...
Heap autocapture: an in-depth review + a better alternative.
Aazar Ali Shad
Guide to Auto-Capture in SaaS: Benefits, Use Cases and Tools
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- My Bibliography
- Collections
- Citation manager
Save citation to file
Email citation, add to collections.
- Create a new collection
- Add to an existing collection
Add to My Bibliography
Your saved search, create a file for external citation management software, your rss feed.
- Search in PubMed
- Search in NLM Catalog
- Add to Search
Descriptive and Inferential Statistics in Nursing Research
Affiliation.
- 1 Courtney Keeler is an associate professor and Alexa Colgrove Curtis is associate dean of academic affairs and faculty development, both at the University of San Francisco School of Nursing and Health Professions. Contact author: Courtney Keeler, [email protected] . Bernadette Capili, PhD, NP-C, is the column coordinator: [email protected] . This manuscript was supported in part by grant No. UL1TR001866 from the National Institutes of Health's National Center for Advancing Translational Sciences Clinical and Translational Science Awards Program. The authors have disclosed no potential conflicts of interest, financial or otherwise.
- PMID: 38126835
- DOI: 10.1097/01.NAJ.0001004944.46230.42
Editor's note: This is the 19th article in a series on clinical research by nurses. The series is designed to be used as a resource for nurses to understand the concepts and principles essential to research. Each column will present the concepts that underpin evidence-based practice-from research design to data interpretation. To see all the articles in the series, go to https://links.lww.com/AJN/A204.
Copyright © 2024 Wolters Kluwer Health, Inc. All rights reserved.
PubMed Disclaimer
Similar articles
- Introduction to Statistical Hypothesis Testing in Nursing Research. Keeler C, Curtis AC. Keeler C, et al. Am J Nurs. 2023 Jul 1;123(7):53-55. doi: 10.1097/01.NAJ.0000944936.37768.29. Am J Nurs. 2023. PMID: 37345783
- Sample Size Planning in Quantitative Nursing Research. Curtis AC, Keeler C. Curtis AC, et al. Am J Nurs. 2023 Nov 1;123(11):42-46. doi: 10.1097/01.NAJ.0000995360.84994.3b. Am J Nurs. 2023. PMID: 37882402
- An Introduction to Implementing and Conducting the Study. Capili B, Anastasi JK. Capili B, et al. Am J Nurs. 2024 May 1;124(5):58-61. doi: 10.1097/01.NAJ.0001016388.26001.50. Epub 2024 Apr 25. Am J Nurs. 2024. PMID: 38661704
- How Does Research Start? Capili B. Capili B. Am J Nurs. 2020 Oct;120(10):41-44. doi: 10.1097/01.NAJ.0000718644.96765.b3. Am J Nurs. 2020. PMID: 32976154 Free PMC article. Review.
- Interpretation and use of statistics in nursing research. Giuliano KK, Polanowicz M. Giuliano KK, et al. AACN Adv Crit Care. 2008 Apr-Jun;19(2):211-22. doi: 10.1097/01.AACN.0000318124.33889.6e. AACN Adv Crit Care. 2008. PMID: 18560290 Review.
- Keeler C, Curtis AC. Introduction to statistical hypothesis testing in nursing research. Am J Nurs 2023;123(7):53–5.
- Global Health Observatory. Overweight prevalence among children under 5 years of age (% weight-for-height >+2 SD), survey-based estimates . Geneva, Switzerland: World Health Organization; 2023 Apr 17. https://www.who.int/data/gho/data/indicators/indicator-details/GHO/gho-j... ).
- Curtis AC, Keeler C. Sampling design in nursing research. Am J Nurs 2021;121(3):53–7.
- Keeler C, et al. The association of California's Proposition 56 tobacco tax increase with smoking behavior across racial and ethnic groups and by income. Nicotine Tob Res 2021;23(12):2091–101.
- California Department of Public Health, Chronic Disease Surveillance and Research Branch. California Behavioral Risk Factor Surveillance System (BRFSS) . 2023. https://www.cdph.ca.gov/Programs/CCDPHP/DCDIC/CDSRB/Pages/BRFSS.aspx?TSP... .
- Search in MeSH
Related information
Linkout - more resources, full text sources.
- Ovid Technologies, Inc.
- Wolters Kluwer

- Citation Manager
NCBI Literature Resources
MeSH PMC Bookshelf Disclaimer
The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.

IMAGES
COMMENTS
While descriptive statistics summarize data, inferential statistics help you come to conclusions and make predictions based on your data.
Statistical analysis is a method of aggregating numeric data and drawing inferences about variables. Statistical procedures may be broadly classified into (1) statistics that describe data—descriptive statistics; and (2) statistics that make inferences about more general situations beyond the actual data set—inferential statistics.
Learn how to use numbers in qualitative research from this article, which discusses the benefits and challenges of integrating quantitative and qualitative data.
Qualitative research collects data qualitatively, and the method of analysis is also primarily qualitative. This often involves an inductive exploration of the data to identify recurring themes, patterns, or concepts and then describing and interpreting those categories. Of course, in qualitative research, the data collected qualitatively can ...
When a qualitative researcher resorts to the inferential approach, they generally are doing so because they do not have an exact idea of the answer that would result from a directed question or a graphical representation. The inferential approach allows them to infer a probability based on the information that is available to them.
Inferential Statistics Examples. Sure, inferential statistics are used when making predictions or inferences about a population from a sample of data. Here are a few real-time examples: Medical Research: Suppose a pharmaceutical company is developing a new drug and they're currently in the testing phase.
Descriptive statistics [ 4] try to describe the relationship between variables in a sample or population. Descriptive statistics provide a summary of data in the form of mean, median and mode. Inferential statistics [ 4] use a random sample of data taken from a population to describe and make inferences about the whole population.
If you're new to quantitative data analysis, one of the many terms you're likely to hear being thrown around is inferential statistics. In this post, we'll provide an introduction to inferential stats, using straightforward language and loads of examples .
To answer such questions, researchers use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research.
Summary This chapter discusses research design, which is the attempt to create a structure for classifying and comparing data patterns and introduces inferential statistics as the way to understand how accessible data can help to explain unknown relationships and social realities.
Typically, in education and psychology research, the investigator collects data and subsequently performs descriptive and inferential statistics. For example, a researcher might compute group means and use the null hypothesis significance testing procedure ...
The answer to this question is that they use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research.
Inferential statistics in research draws conclusions that cannot be derived from descriptive statistics, i.e. to infer population opinion from sample data.
Inferential statistics involves the use of a sample (1) to estimate some characteristic in a large population; and (2) to test a research hypothesis about a given population. To appropriately estimate a population characteristic, or parameter, a random and unbiased sample must be drawn from the population of interest.
Qualitative data is a term used by different people to mean different things. I have a couple of statistics texts that refer to categorical data as qualitative and describe various statistical ...
Obviously, you can describe descriptive statistics in qualitative analysis but in case of inferential statistics--it has less precision as seen most qualitative studies sample size is not ...
We recommend that we should use, communicate, and teach inferential statistical methods as describing logical relations between assumptions and data (as detailed in the Appendix), rather than as providing generalizable inferences about universal populations.
Descriptive Statistics Statistics can be broadly divided into descriptive statistics and inferential statistics. [ 3, 4] Descriptive statistics give a summary about the sample being studied without drawing any inferences based on probability theory.
It introduces the common statistical tests that comprise inferential statistics, and explains the use of parametric and non-parametric statistics. To do this, the paper reviews relevant literature, and provides a checklist of points to consider before and after applying statistical tests to a data set. The paper provides a glossary of relevant ...
The answer to this question is that they use a set of techniques called inferential statistics, which is what this chapter is about. We focus, in particular, on null hypothesis testing, the most common approach to inferential statistics in psychological research.
The tasks were: 1) comparing research scenarios from the perspective of choosing a statistical technique, and 2) direct comparison of statistical techniques. The framework was based on expert knowledge in inferential statistics using the repertory grid technique for data collection.
In this chapter we will learn something about both univariate descriptive statistics (statistics that describe single variables in a sample) and univariate inferential statistics (statistics that permit inferences about those variables in the larger population from which the sample was drawn).
The methods for analyzing quantitative data are descriptive and inferential statistics. Choosing the right analysis method depends on the type of data collected and the specific research questions or hypotheses. These are the steps to conduct quantitative data analysis: 1. Defining goals and KPIs. 2. Collecting and cleaning data. 3. Visualizing ...
Abstract. Editor's note: This is the 19th article in a series on clinical research by nurses. The series is designed to be used as a resource for nurses to understand the concepts and principles essential to research. Each column will present the concepts that underpin evidence-based practice-from research design to data interpretation.